giúp e với aa, e cảm ơn nhiềuu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
7 tháng 7 2021
Lời giải:
$A=1+\frac{1}{\sqrt{x}-3}$
Để $A$ max thì $\sqrt{x}-3$ phải dương và nhỏ nhất.
Với $x$ nguyên, để $\sqrt{x}-3$ dương và nhỏ nhất thì $x=10$
Khi đó, $A_{\max}=1+\frac{1}{\sqrt{10}-3}=4+\sqrt{10}$
------------------
$B=1+\frac{1}{\sqrt{x}-2}$.
Lập luận tương tự phần a, ta thấy với $x$ nguyên không âm thì $\sqrt{x}-2$ đạt giá trị dương nhỏ nhất tại $x=5$
$\Rightarrow B_{\max}=1+\frac{1}{\sqrt{5}-2}=3+\sqrt{5}$
PH
1
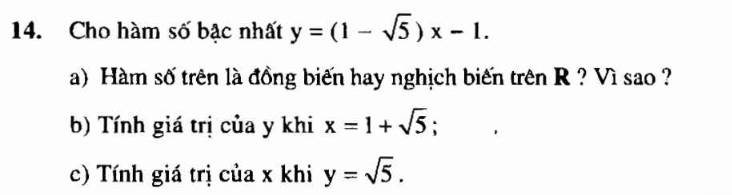giúp e với aa, e cảm ơnn
31 tháng 8 2021
Câu 1:
Thay x=0 vào y=x+1, ta được:
y=0+1=1
Thay y=0 vào y=x+1, ta được:
x+1=0
hay x=-1
vậy: A(-1;0); B(0;1)
\(AB=\sqrt{\left(-1-0\right)^2+\left(0-1\right)^2}=\sqrt{2}\)
\(C_{OAB}=OA+OB+AB=2+\sqrt{2}\)
\(S_{OAB}=\dfrac{OA\cdot OB}{2}=\dfrac{1}{2}\)
giúp e với aaa, e cảm ơn
giúp e với a, e cảm ơn
HL
1
17 tháng 12 2021
a: \(x=2\sqrt{2}+2-2\sqrt{2}+2=4\)
Thay x=4 vào B, ta được:
\(B=\dfrac{2-3}{2+1}=\dfrac{-1}{3}\)
19 tháng 3 2022
\(K=\dfrac{2\sqrt{3a+1}+2\sqrt{3b+1}+2\sqrt{3c+1}}{2}\)\(\le\)\(\dfrac{3a+1+4+3b+1+4+3c+1+4}{4}=\dfrac{24}{4}=6\)
Vậy \(K_{max}=6\)
Dấu bằng xảy ra khi a=b=c=1
a) Hàm số trên nghịch biến trên R vì:
\(1< \sqrt{5}\Rightarrow1-\sqrt{5}< 0\)
\(\Rightarrow\) hệ số \(a< 0\)
b) Khi \(x=1+\sqrt{5}\)
\(y=\left(1-\sqrt{5}\right)\left(1+\sqrt{5}\right)-1\)
\(y=1^2-\left(\sqrt{5}\right)^2-1\)
\(y=1-5-1\)
\(y=-5\)
c) Khi \(y=\sqrt{5}\) khi và chỉ khi:
\(\left(1-\sqrt{5}\right)x-1=\sqrt{5}\)
\(\Leftrightarrow\left(1-\sqrt{5}\right)x=1+\sqrt{5}\)
\(\Leftrightarrow x=\dfrac{1+\sqrt{5}}{1-\sqrt{5}}\)
\(\Leftrightarrow x=\dfrac{\left(1+\sqrt{5}\right)^2}{1-5}\)
\(\Leftrightarrow x=-\dfrac{3+\sqrt{5}}{2}\)