K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 2 2022
\(\int\left(\dfrac{7}{cos^2x}+cosx-3^x+2\right)dx=7tanx+sinx-\dfrac{3^x}{ln3}+2x+C\)
LT
0
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 9 2021
20.
\(y'=\dfrac{a^2+b^2+1}{\left(x+a\right)^2}>0\Rightarrow\) hàm đồng biến trên các khoảng xác định
\(\Rightarrow y_{min}\) khi \(x_{min}\Rightarrow x=a\)
21.
\(f'\left(x\right)=3x^2+m^2\ge0\Rightarrow\) hàm đồng biến trên R
\(\Rightarrow f\left(x\right)_{min}=f\left(1\right)=m^2+19\)
\(\Rightarrow m^2+19\le20\)
\(\Rightarrow m^2\le1\Rightarrow m=\left\{-1;0;1\right\}\)
Có 3 giá trị nguyên
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
Xét \(I_1=\int\limits^{\dfrac{\pi}{3}}_{\dfrac{\pi}{4}}\dfrac{f\left(tanx\right)}{cos^2x}dx=\int\limits^{\dfrac{\pi}{3}}_{\dfrac{\pi}{4}}f\left(tanx\right)d\left(tanx\right)\)
Đặt \(tanx=t\Rightarrow t\in\left[1;\sqrt{3}\right]\Rightarrow f\left(t\right)=2t^3-t\)
\(I_1=\int\limits^{\sqrt{3}}_1f\left(t\right)dt=\int\limits^{\sqrt{3}}_1\left(2t^3-t\right)dt=3\)
Xét \(I_2=\int\limits^{\sqrt{e-1}}_0\dfrac{xf\left(ln\left(x^2+1\right)\right)}{x^2+1}dx=\dfrac{1}{2}\int\limits^{\sqrt{e-1}}_0f\left(ln\left(x^2+1\right)\right).d\left[ln\left(x^2+1\right)\right]\)
Đặt \(ln\left(x^2+1\right)=t\Rightarrow t\in\left[0;1\right]\Rightarrow f\left(t\right)=-3t+4\)
\(I_2=\dfrac{1}{2}\int\limits^1_0\left(-3t+4\right)dt=\dfrac{5}{4}\)
\(\Rightarrow I=3+\dfrac{5}{4}=\dfrac{17}{4}\Rightarrow P=21\)
HT
16 tháng 7 2023
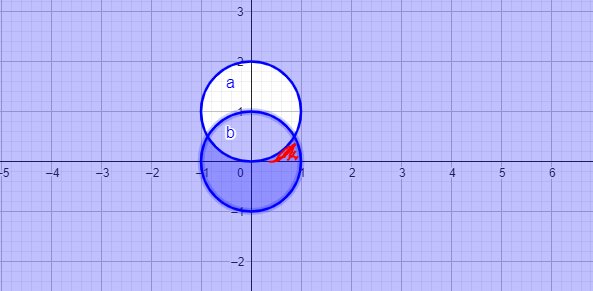
Giao điểm của 2 pt đường tròn \(\left(\dfrac{\sqrt{3}}{2};\dfrac{1}{2}\right)\)
\(\left\{{}\begin{matrix}x=r\cos\varphi\\y=r\sin\varphi\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}r\in\left[2\sin\varphi;1\right]\\\varphi\in\left[0;\dfrac{\pi}{6}\right]\\\left|J\right|=r\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^{\dfrac{\pi}{6}}_0d\varphi\int\limits^1_{2\sin\varphi}\sqrt{r^2}.rdr=\int\limits^{\dfrac{\pi}{6}}_0d\varphi\int\limits^1_{2\sin\varphi}r^2dr=\dfrac{1}{3}\int\limits^{\dfrac{\pi}{6}}_0\left(1-8\sin^3\varphi\right)d\varphi=...\)
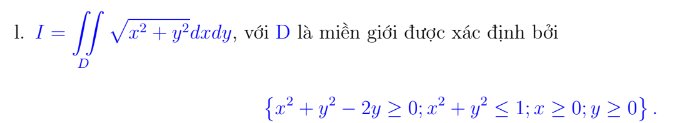
- Với \(x=2\) chuỗi hiển nhiên hội tụ
- Với \(x\ne2\):
\(u_{n+1}=\dfrac{\left(-1\right)^{n+1}\left(x-2\right)^{2n+2}}{\left(n^2+2n+2\right)4^{n+1}}\)
\(\lim\limits\left|\dfrac{u_{n+1}}{u_n}\right|=\lim\left|\dfrac{\left(-1\right)^{n+1}.\left(x-2\right)^{2n+2}}{\left(n^2+2n+2\right).4^{n+1}}.\dfrac{\left(n^2+1\right)4^n}{\left(-1\right)^n.\left(x-2\right)^{2n}}\right|\)
\(=\left|\dfrac{\left(x-2\right)^2}{4}\right|< 1\)
\(\Rightarrow-2< x-2< 2\Rightarrow0< x< 4\)
- Với \(x=4\) chuỗi trở thành: \(\sum\limits^{\infty}_{n=1}\dfrac{\left(-1\right)^n.2^{2n}}{\left(n^2+1\right).4^n}=\sum\limits^{\infty}_{n=1}\dfrac{\left(-1\right)^n}{n^2+1}\) hội tụ theo tiêu chuẩn Leibniz
- Với \(x=0\) chuổi trở thành \(\sum\limits^{\infty}_{n=1}\dfrac{\left(-1\right)^n}{n^2+1}\) giống như trên hội tụ theo t/c Leibniz
Vậy miền hội tụ của chuỗi là \(x\in\left[0;4\right]\)
e cảm ơn ạ