
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




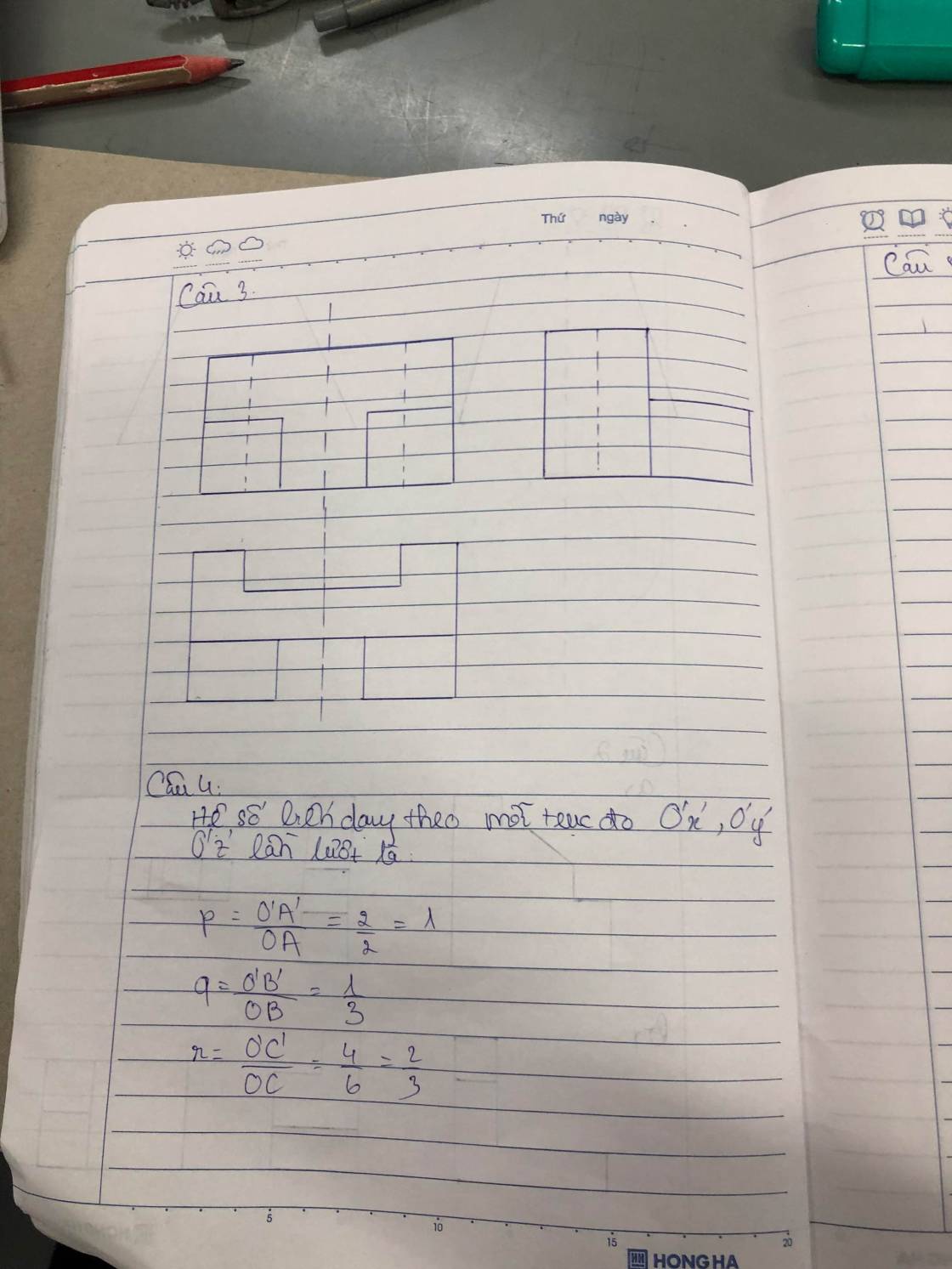
Hệ số biến dạng theo mỗi trục đo O'x', O'y', O'z' lần lượt là:
p=O'A'OA=22=1�=�'�'��=22=1;
q=O'B'OB=13�=�'�'��=13;
r=O'C'OC=46=23�=�'�'��=46=23.


a)

Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng lớn (dần tới \( + \infty \)).
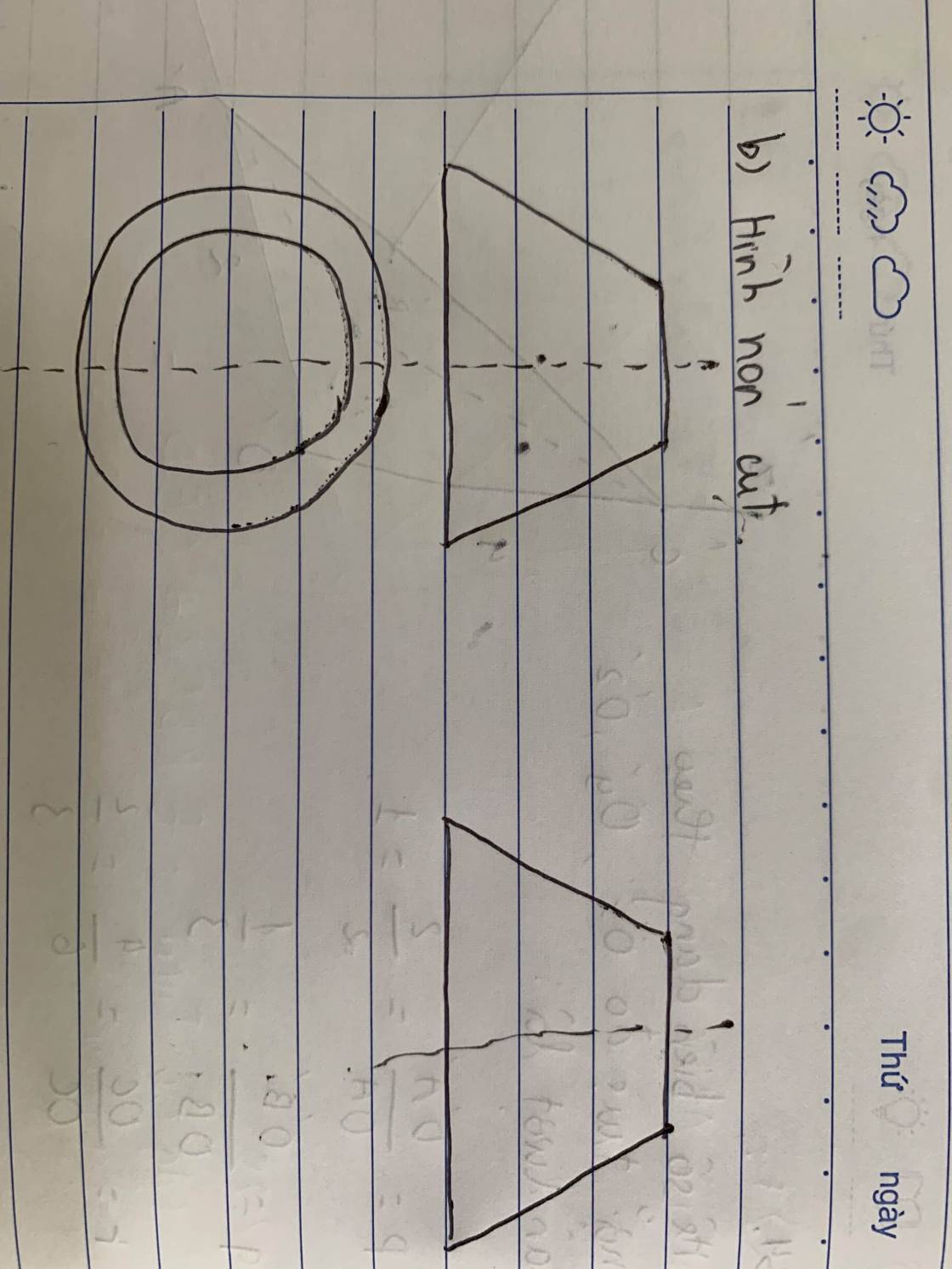
b)

Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng bé (dần tới \( - \infty \)).

a.
\(sin\left(2x-\dfrac{\pi}{4}\right)=-1\)
\(\Leftrightarrow2x-\dfrac{\pi}{4}=-\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{8}+k\pi\) (1)
\(-\dfrac{\pi}{3}\le x\le\dfrac{7\pi}{3}\Rightarrow-\dfrac{\pi}{3}\le-\dfrac{\pi}{8}+k\pi\le\dfrac{7\pi}{3}\)
\(\Rightarrow-\dfrac{5}{24}\le k\le\dfrac{59}{24}\Rightarrow k=\left\{0;1;2\right\}\)
Thế vào (1) \(\Rightarrow x=\left\{-\dfrac{\pi}{8};\dfrac{7\pi}{8};\dfrac{15\pi}{8}\right\}\)






 Giúp e vs ạ
Giúp e vs ạ



c.
Gọi E là trung điểm AD \(\Rightarrow EM\) là đường trung bình tam giác SAD
\(\Rightarrow\left\{{}\begin{matrix}EM=\dfrac{1}{2}SA=a\\EM||SA\Rightarrow EM\perp\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow EC\) là hình chiếu vuông góc của CM lên (ABCD)
\(\Rightarrow\widehat{MCE}\) là góc giữa SM và (ABCD)
\(ED=\dfrac{1}{2}AD=a\Rightarrow EC=\sqrt{CD^2+ED^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{MCE}=\dfrac{EM}{EC}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{MCE}=...\)
e.
Gọi O là trung điểm BD, qua A kẻ đường thẳng song song BD cắt OE kéo dài tại F
\(\Rightarrow ABOF\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow\left\{{}\begin{matrix}AF=OB=\dfrac{1}{2}BD\\AF||BD\end{matrix}\right.\)
Lại có MN là đường trung bình tam giác SBD \(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}BD\\MN||BD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}MN=AF\\MN||AF\end{matrix}\right.\) \(\Rightarrow ANMF\) là hình bình hành
\(\Rightarrow AN||MF\Rightarrow\left(AN;CM\right)=\left(AN;MF\right)=\widehat{CMF}\) nếu nó ko tù hoặc bằng góc bù của nó nếu \(\widehat{CMF}\) là góc tù
Ta có: \(MF=AN=\dfrac{a\sqrt{5}}{2}\) ; \(CM=\sqrt{CE^2+EM^2}=a\sqrt{3}\)
ABOF là hình bình hành nên AODF cũng là hình bình hành \(\Rightarrow E\) là tâm hình bình hành
\(\Rightarrow EF=OF=\dfrac{AB}{2}=\dfrac{a}{2}\)
Gọi G là giao điểm OE và BC \(\Rightarrow FG=EG+EF=a+\dfrac{a}{2}=\dfrac{3a}{2}\)
\(\Rightarrow CF=\sqrt{FG^2+CG^2}=\dfrac{a\sqrt{13}}{2}\)
ĐỊnh lý hàm cos:
\(cos\widehat{CMF}=\dfrac{CM^2+MF^2-CF^2}{2CM.MF}=\dfrac{\sqrt{15}}{15}\Rightarrow\widehat{CMF}\)