
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bán kính trụ: \(12,2:2=6,1\left(cm\right)\)
Thể tích trụ:
\(V=\pi.6,1^2.6=701,49\left(cm^3\right)\approx0,7\left(dm^3\right)\)
Do đó có thể xếp được:
\(0,7:0,1=7\) miếng thịt


3:
Tháng 4 phải trả:
\(50\cdot1678+50\cdot1734+100\cdot2014+100\cdot2536+1\cdot2834=628434\left(đồng\right)\)
Tháng 5 phải trả:
\(50\cdot1678+50\cdot1734+100\cdot2014+98\cdot2536=620528\left(đồng\right)\)
=>Giảm 1,3%

\(26,\\ a,\sin45^0=\cos45^0< \sin50^025'< \sin57^048'=\cos32^012'< \sin72^0=\cos18^0< \sin75^0\\ b,\tan37^026'< \tan47^0< \tan58^0=\cot32^0< \tan63^0< \tan66^019'=\cot23^041'\\ 27,\\ A=\dfrac{\left(\sin^226^0+\sin^264^0\right)+2\left(\cos^215^0+\cos^275^0\right)}{\left(\sin^255^0+\cos^255^0\right)+\left(\sin^242^0+\cos^242^0\right)}-\dfrac{\tan81^0}{2\tan81^0}\\ A=\dfrac{\left(\sin^226^0+\cos^226^0\right)+2\left(\sin^215^0+\cos^215^0\right)}{1+1}-\dfrac{1}{2}\\ A=\dfrac{1+2}{2}-\dfrac{1}{2}=2-\dfrac{1}{2}=\dfrac{3}{2}\)
\(28,\\ \sin^2\alpha=1-\cos^2\alpha=1-\dfrac{1}{2}=\dfrac{1}{2}\\ \Leftrightarrow\sin\alpha=\dfrac{\sqrt{2}}{2}\)


\(x+\sqrt{4-x^2}=2\)
\(\Leftrightarrow4-x^2=\left(2-x\right)^2\)
\(\Leftrightarrow4-x^2=4-8x+x^2\)
\(\Leftrightarrow4-x^2-4+8x-x^2=0\)
\(\Leftrightarrow8x-2x^2=0\)
\(\Leftrightarrow2x\left(4-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\4-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
\(x+\sqrt{1-x^2}=1\)
\(\Leftrightarrow1-x^2=\left(1-x\right)^2\)
\(\Leftrightarrow1-x^2=1-2x+x^2\)
\(\Leftrightarrow1-x^2-1+2x-x^2=0\)
\(\Leftrightarrow2x-2x^2=0\)
\(\Leftrightarrow2x\left(1-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\1-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

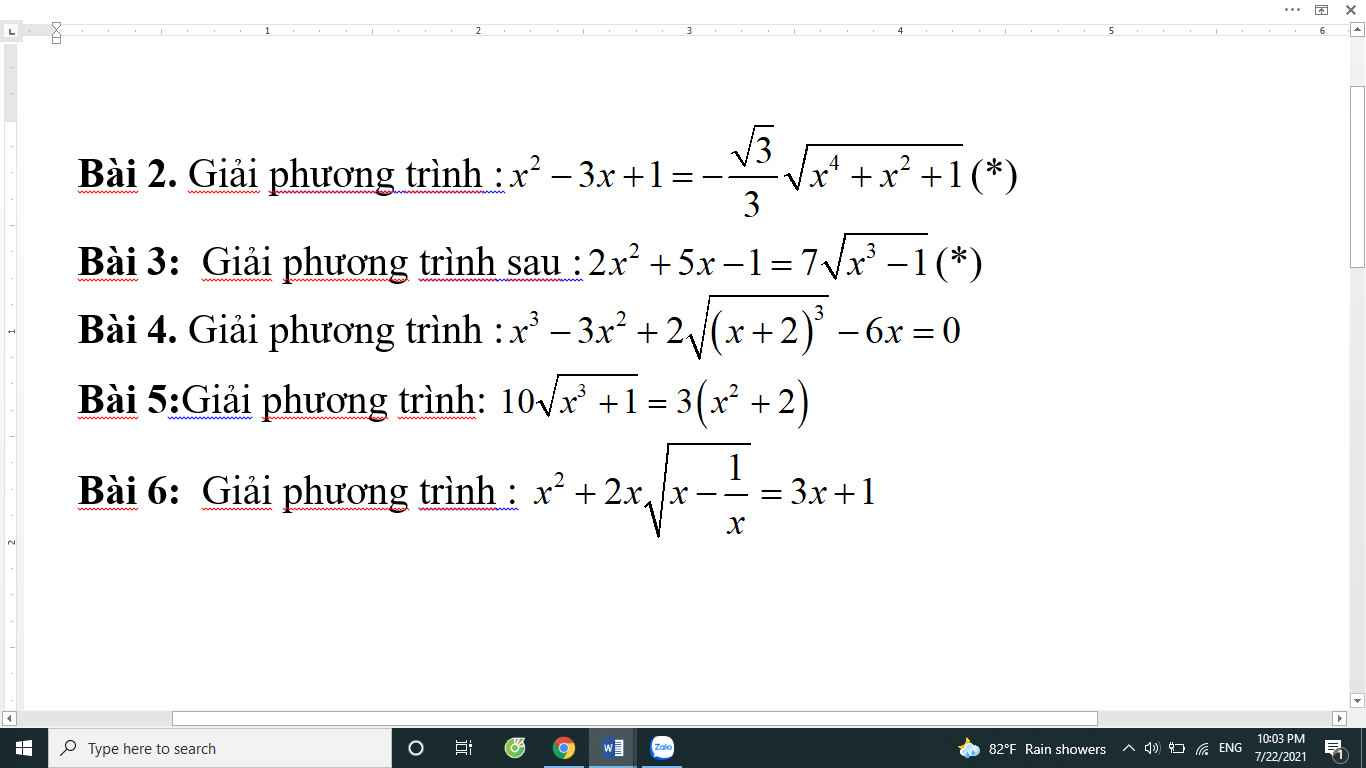
Đặt \(\sqrt{x^2-x+1}=a>0;\sqrt{x^2+x+1}=b>0\).
\(PT\Leftrightarrow2a^2-b^2=-\dfrac{\sqrt{3}}{3}ab\)
\(\Leftrightarrow\left(a+\dfrac{\sqrt{3}}{2}b\right)\left(2a-\dfrac{2\sqrt{3}}{3}b\right)=0\)
\(\Leftrightarrow2a-\dfrac{2\sqrt{3}}{3}b=0\) (Do a, b > 0)
\(\Leftrightarrow2\sqrt{x^2-x+1}=\dfrac{2\sqrt{3}}{3}\sqrt{x^2+x+1}\)
\(\Leftrightarrow x^2-x+1=\dfrac{1}{3}\left(x^2+x+1\right)\Leftrightarrow2x^2-4x+2=0\Leftrightarrow x=1\).
Vậy x = 1

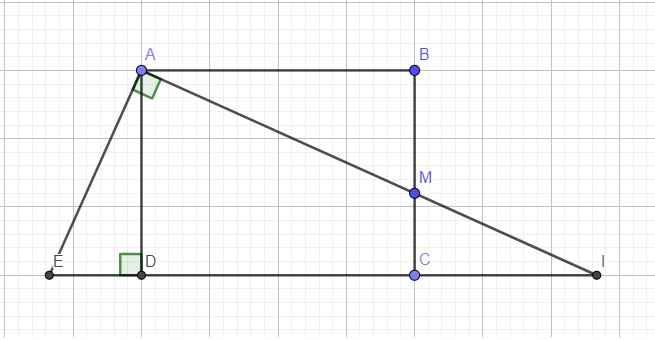
Qua A kẻ đường thẳng vuông góc AI cắt CD kéo dài tại E
Ta có \(\widehat{EAD}=\widehat{MAB}\) (cùng phụ \(\widehat{DAM}\))
\(\Rightarrow\Delta_vADE\sim\Delta_vABM\Rightarrow\dfrac{AE}{AM}=\dfrac{AD}{AB}=\dfrac{3}{4}\)
\(\Rightarrow\dfrac{1}{AE}=\dfrac{4}{3AM}\)
Áp dụng hệ thức lượng trong tam giác vuông AEI:
\(\dfrac{1}{AD^2}=\dfrac{1}{AE^2}+\dfrac{1}{AI^2}\Leftrightarrow\dfrac{1}{\left(\dfrac{3}{4}AB\right)^2}=\left(\dfrac{4}{3AM}\right)^2+\dfrac{1}{AI^2}\)
\(\Leftrightarrow\dfrac{1}{AB^2}=\dfrac{1}{AM^2}+\dfrac{9}{16AI^2}\)
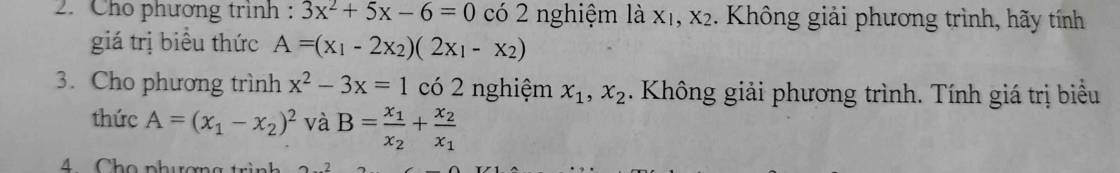


 làm giúp e câu 3, 4 với ạ
làm giúp e câu 3, 4 với ạ



\(x^2-3x=1\Leftrightarrow x^2-3x-1=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=1\\x_1x_2=\dfrac{c}{a}=-1\end{matrix}\right.\)
\(A=\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=1^2-4.\left(-1\right)\)
\(=5\)
\(B=\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=\dfrac{x_1^2+x_2^2}{x_1x_2}=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{x_1x_2}=\dfrac{1^2-2.\left(-1\right)}{\left(-1\right)}=-4\)
Mình rối quá bạn có thể ghi vào tập giúp mik đc kh ạ