K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
\(\lim\limits_{x\rightarrow+\infty}\left(ax-\sqrt{x^2+bx+2}\right)=\lim\limits_{x\rightarrow+\infty}x\left(a-\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}\right)\)
Nếu \(a\ne1\Rightarrow\lim\limits_{x\rightarrow+\infty}\left(a-\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}\right)=a-1\ne0\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}x\left(a-\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}\right)=\infty\) ko thỏa mãn giả thiết \(=4\) (hữu hạn)
\(\Rightarrow a=1\)
\(\lim\limits_{x\rightarrow+\infty}\left(x-\sqrt{x^2+bx+2}\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{-bx-2}{x+\sqrt{x^2+bx+2}}=\lim\limits_{x\rightarrow+\infty}\dfrac{-b-\dfrac{2}{x}}{1+\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}}=-\dfrac{b}{2}\)
\(\Rightarrow-\dfrac{b}{2}=4\Rightarrow b=-8\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
21.
Giới hạn đã cho hữu hạn khi và chỉ khi \(a=1\)
Khi đó:
\(\lim\limits_{x\rightarrow+\infty}\left(x-\sqrt{x^2+bx+2}\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2-\left(x^2+bx+2\right)}{x+\sqrt{x^2+bx+2}}=\lim\limits_{x\rightarrow+\infty}\dfrac{-bx-2}{x+\sqrt{x^2+bx+2}}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{-b-\dfrac{2}{x}}{1+\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}}=\dfrac{-b}{2}\)
\(\Rightarrow-\dfrac{b}{2}=4\Rightarrow b=-8\)
\(\Rightarrow a+b=1-8=-7\)
22.
B sai, do các cạnh bên của chóp đều tạo với đáy các góc bằng nhau
21 tháng 6 2023
21:
\(y'=\dfrac{\left(x^2-3x+5\right)'\left(x+2\right)-\left(x+2\right)'\left(x^2-3x+5\right)}{\left(x+2\right)^2}\)
\(=\dfrac{\left(2x-3\right)\left(x+2\right)-\left(x^2-3x+5\right)}{\left(x+2\right)^2}\)
\(=\dfrac{2x^2+4x-3x-6-x^2+3x-5}{\left(x+2\right)^2}=\dfrac{x^2+4x-11}{\left(x+2\right)^2}\)
17:
Khi x<>0 thì \(\lim\limits_{x\rightarrow0}f\left(x\right)=\lim\limits_{x\rightarrow0}\dfrac{1+4x-1}{\sqrt{1+4x}+1}\cdot\dfrac{1}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{4}{\sqrt{1+4x}+1}=\dfrac{4}{1+1}=\dfrac{4}{2}=2\)
=>Chọn B
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 12 2021
\(\Leftrightarrow2sinx.cosx-2m.cosx+m-sinx=0\)
\(\Leftrightarrow2cosx\left(sinx-m\right)-\left(sinx-m\right)=0\)
\(\Leftrightarrow\left(2cosx-1\right)\left(sinx-m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\dfrac{1}{2}\Rightarrow x=\dfrac{\pi}{3}\\sinx=m\end{matrix}\right.\)
Pt có 2 nghiệm thuộc đoạn đã cho khi \(sinx=m\) có đúng 1 nghiệm thuộc đoạn đã cho
\(\Rightarrow\left[{}\begin{matrix}m=1\\-\dfrac{\sqrt{2}}{2}\le m< 0\end{matrix}\right.\)
\(\Rightarrow\) Có 1 giá trị nguyên của m
AH
Akai Haruma
Giáo viên
25 tháng 10 2021
Lời giải:
Trong khoảng $[\frac{-\pi}{2}; \frac{-\pi}{3}]$ $x$ càng lớn thì $\sin x$ càng lớn
Do đó:
$y_{\min}=y(\frac{-\pi}{2})=-1$
$y_{\max}=y(\frac{-\pi}{3})=\frac{-\sqrt{3}}{2}$
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
\(y'=\dfrac{-5}{\left(x-3\right)^2}\)
\(\Rightarrow y'\left(4\right)=\dfrac{-5}{\left(4-3\right)^2}=-5\) ; \(y\left(4\right)=\dfrac{2.4-1}{4-3}=7\)
Phương trình tiếp tuyến tại điểm có hoành độ \(x=4\) là:
\(y=-5\left(x-4\right)+7=-5x+27\)
17 tháng 8 2021
sinx - sin3x - \(\sqrt{3}\left(cosx+sin3x\right)=0\)
⇔ sinx - \(\sqrt{3}cosx-\left(1+\sqrt{3}\right)sin3x\) = 0
⇔ \(2sin\left(x-\dfrac{\pi}{3}\right)-\left(1-\sqrt{3}\right)sin\left(\pi-3x\right)\) = 0
⇔ \(2sin\left(x-\dfrac{\pi}{3}\right)+\left(1-\sqrt{3}\right)sin\left(3x-\pi\right)=0\)
⇔ \(2sin\left(x-\dfrac{\pi}{3}\right)+\left(1-\sqrt{3}\right)sin3\left(x-\dfrac{\pi}{3}\right)=0\)
Đặt a = x - \(\dfrac{\pi}{3}\) ta có phương trình mới
2sina + (1 - \(\sqrt{3}\))sin3a = 0 (1)
Sử dụng công thức sin3a = 3sina - 4sin3a đưa (1) về phương trình bậc 3 ẩn là a. Từ a suy ra x
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 11 2021
Đáy là bát giác đều (8 cạnh) nên chóp có 8 mặt bên
Cộng thêm mặt đáy nữa nên ta sẽ có tổng cộng 9 mặt
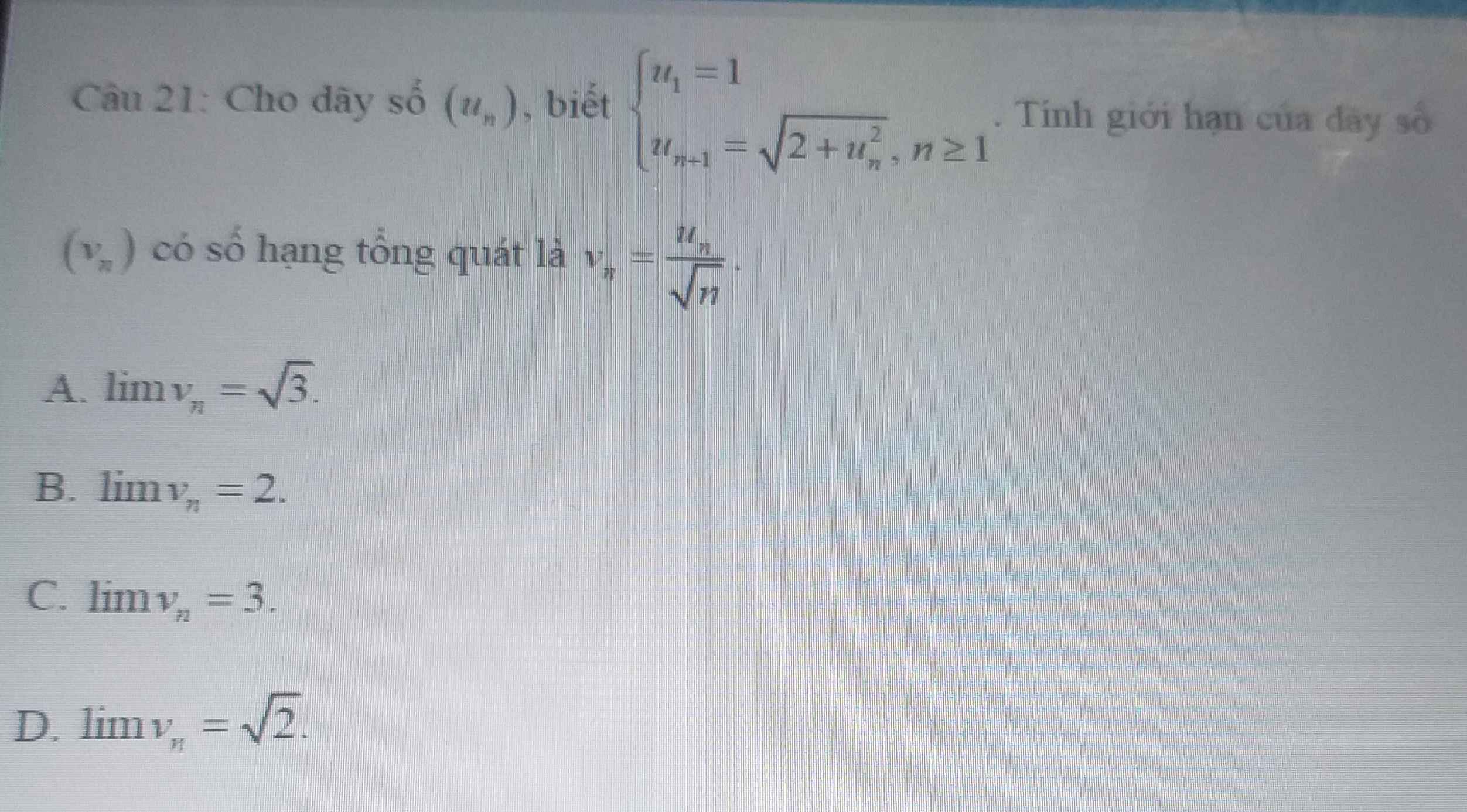
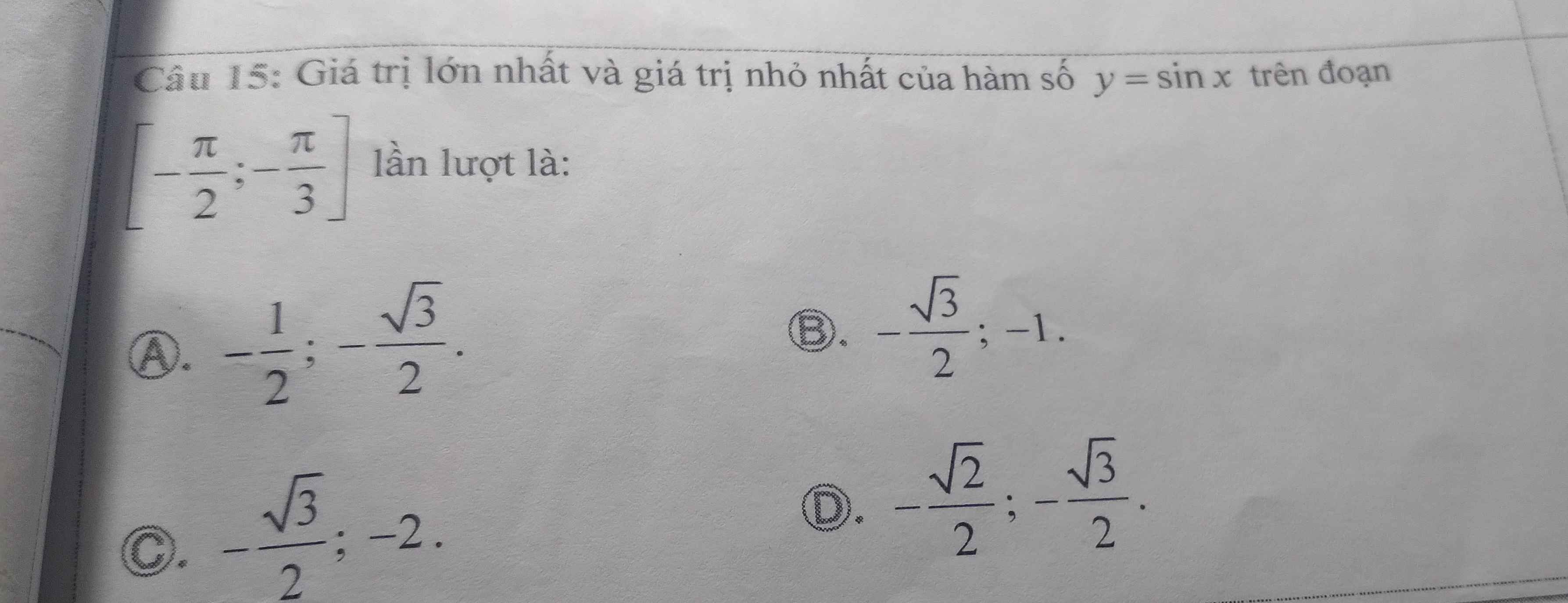
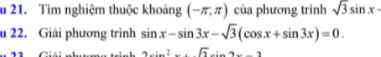
\(u_1=1=\sqrt{2.0+1}\)
\(u_2=\sqrt{2+u_1^2}=\sqrt{3}=\sqrt{2.1+1}\)
\(u_3=\sqrt{2+u_2^2}=\sqrt{5}=\sqrt{2.2+1}\)
\(\Rightarrow u_n=\sqrt{2\left(n-1\right)+1}=\sqrt{2n-1}\)
\(\Rightarrow v_n=\sqrt{\dfrac{2n-1}{n}}=\sqrt{2-\dfrac{1}{n}}\)
\(\Rightarrow\lim\left(v_n\right)=\lim\sqrt{2-\dfrac{1}{n}}=\sqrt{2}\)