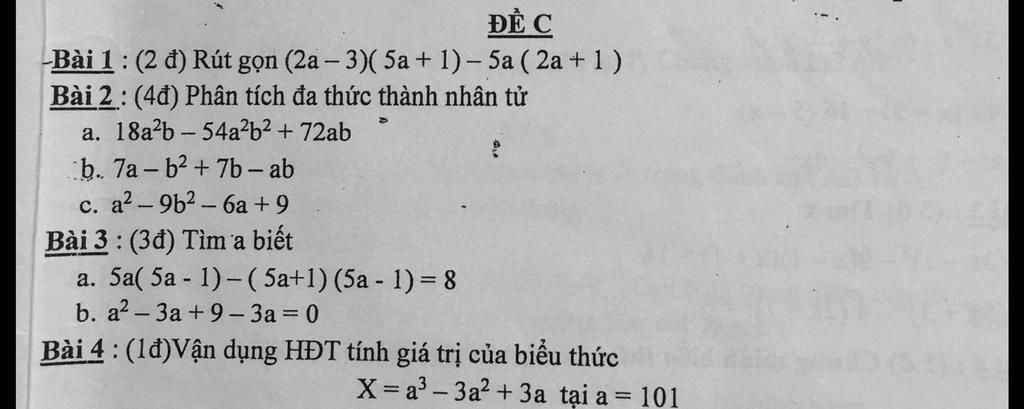K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 8 2021
Bài 2:
a:\(18a^2b-54a^2b^2+72ab\)
\(=18ab\left(a-3ab+4\right)\)
b: \(7a-b^2+7b-ab\)
\(=7\left(a+b\right)-b\left(a+b\right)\)
\(=\left(a+b\right)\left(7-b\right)\)
c: \(a^2-9b^2-6a+9\)
\(=\left(a-3\right)^2-9b^2\)
\(=\left(a-3-3b\right)\left(a-3+3b\right)\)
Bài 4:
Ta có: \(X=a^3-3a^2+3a\)
\(=a^3-3a^2+3a-1+1\)
\(=\left(a-1\right)^3+1\)
\(=100^3+1=1000001\)
15 tháng 8 2021
Bài 3:
a: Ta có: \(5a\left(5a-1\right)-\left(5a+1\right)\left(5a-1\right)=8\)
\(\Leftrightarrow25a^2-5a-25a^2+1=8\)
\(\Leftrightarrow5a=-7\)
hay \(a=-\dfrac{7}{5}\)
b: Ta có: \(a^2-3a+9-3a=0\)
\(\Leftrightarrow a\left(a-3\right)-3\left(a-3\right)=0\)
\(\Leftrightarrow\left(a-3\right)^2=0\)
\(\Leftrightarrow a-3=0\)
hay a=3
NL
1
21 tháng 1 2022
Câu 1:
a: x/1.25=3.5/2.5=7/5
=>x=1.75
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{x+y}{4+3}=\dfrac{2.1}{7}=0.3\)
Do đó: x=1,2; y=0,9
28 tháng 9 2021
chu vi hình vuông là
50x4=200cm
độ dài 1 cạnh hình vuông là
50:4=12,5cm
diện tích hình vuông là
12,5x12,5=156,25cm2
23 tháng 2 2022
a: \(P=\dfrac{8}{x\left(x+4\right)}+\dfrac{5x}{x\left(x+4\right)}-\dfrac{2x+8}{x\left(x+4\right)}=\dfrac{8+5x-2x-8}{x\left(x+4\right)}=\dfrac{3}{x+4}\)
b: Thay x=1/2 vào P, ta được:
P=3:9/2=3x2/9=6/9=2/3
23 tháng 2 2022
Với khác 0 ; x khác 4
\(P=\dfrac{8+5x-2x-8}{x\left(x+4\right)}=\dfrac{3x}{x\left(x+4\right)}=\dfrac{3}{x+4}\)
Thay x = 1/2 vào P ta được \(\dfrac{3}{\dfrac{1}{2}+4}=\dfrac{3}{\dfrac{9}{2}}=3:\dfrac{9}{2}=\dfrac{2}{3}\)
LC
1
21 tháng 11 2023
a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔHAC~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>BC=25
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH\cdot25=15^2=225\\AH\cdot25=15\cdot20=300\end{matrix}\right.\)
=>BH=9; AH=12
NV
1
7 tháng 9 2017
(x2 _ 1)3 _ (x4 + x2 + 1) (x2 _ 1)
= x6 _ 1 _ ( x6 + x4 + x2 _ x4 _ x2 _ 1)
= x6 _ 1 _ x6 _ x4 _ x2 + x4 + x2 + 1
= 0
8 tháng 5 2021
ĐKXĐ: \(x\notin\left\{0;-9\right\}\)
Ta có: \(\dfrac{1}{x+9}-\dfrac{1}{x}=\dfrac{1}{5}+\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{20x}{20x\left(x+9\right)}-\dfrac{20\left(x+9\right)}{20x\left(x+9\right)}=\dfrac{4x\left(x+9\right)+5x\left(x+9\right)}{20x\left(x+9\right)}\)
Suy ra: \(4x^2+36x+5x^2+45x=20x-20x-180\)
\(\Leftrightarrow9x^2+81x+180=0\)
\(\Leftrightarrow x^2+9x+20=0\)
\(\Leftrightarrow x^2+4x+5x+20=0\)
\(\Leftrightarrow x\left(x+4\right)+5\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\left(nhận\right)\\x=-5\left(nhận\right)\end{matrix}\right.\)
Vậy: S={-4;-5}
22 tháng 3 2022
Bài 5:
\(x=by+cz;y=ax+cz\)
\(\Rightarrow x-y=by+cz-\left(ax-cz\right)=by-ax\)
\(\Rightarrow x+ax-y-by=0\)
\(\Rightarrow x\left(a+1\right)=y\left(b+1\right)\)
\(\Rightarrow a+1=\dfrac{y\left(b+1\right)}{x}\)
\(y=ax+cz;z=ax+by\)
\(\Rightarrow y-z=ax+cz-\left(ax+by\right)\)
\(\Rightarrow y-z=cz-by\)
\(\Rightarrow y+by-z-cz=0\)
\(\Rightarrow y\left(b+1\right)=z\left(c+1\right)\)
\(\Rightarrow c+1=\dfrac{y\left(b+1\right)}{z}\)
\(\dfrac{1}{1+a}+\dfrac{1}{1+b}+\dfrac{1}{1+c}=\dfrac{1}{\dfrac{y\left(b+1\right)}{x}}+\dfrac{1}{b+1}+\dfrac{1}{\dfrac{y\left(b+1\right)}{z}}=\dfrac{x}{y\left(b+1\right)}+\dfrac{y}{y\left(b+1\right)}+\dfrac{z}{y\left(b+1\right)}=\dfrac{x+y+z}{y\left(b+1\right)}=\dfrac{2\left(ax+by+cz\right)}{by+y}=\dfrac{2\left(ax+by+cz\right)}{by+ax+cz}=2\)