CD
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 1 2022
Bài 1:1×2×3×4×5×6×7×8×9×10 bằng mấy? Bài 2:5×5×5×5×5×5×5×5×5×5=3628800
Bài 2:9×9×9×9×9×9×9×9×9×9 = 3486784401 (bạn k cho mình nha)
CM
17 tháng 8 2017
Chọn A
f ' ( x ) đổi dấu khi x chạy qua -1 và 3 nên hàm số có 2 điểm cực trị.
PT
1
CM
9 tháng 9 2019
Đáp án: B.
Hàm số y = ( x + 1 ) 3 (5 - x) xác định trên R.
y' = - ( x + 1 ) 3 + 3 ( x + 1 ) 2 (5 - x) = 2 ( x + 1 ) 2 (7 - 2x)
y' = 0 ⇔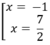 
Bảng biến thiên
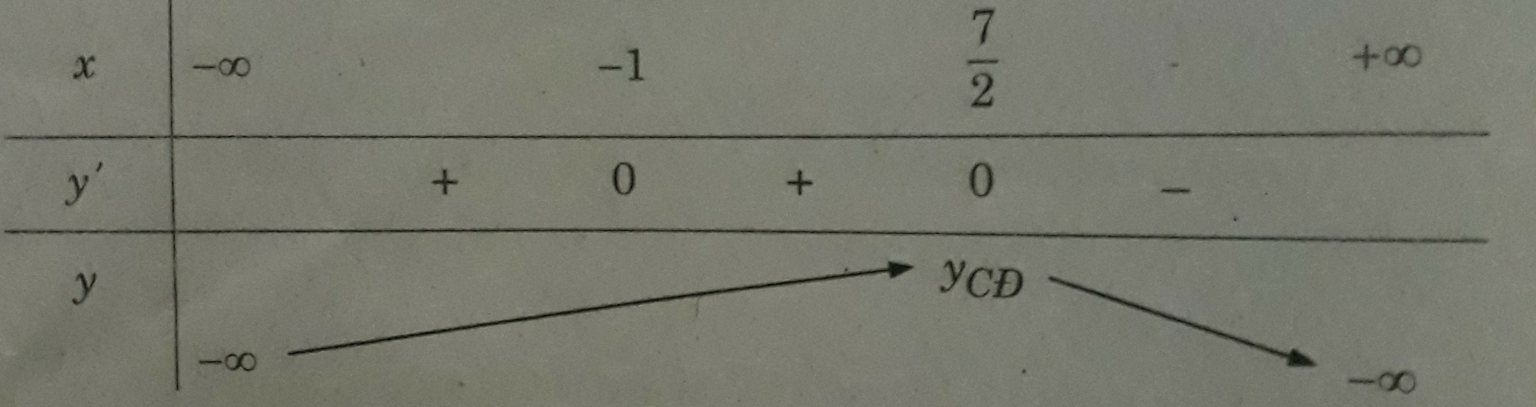
Suy ra hàm số chỉ có một cực trị (là cực đại)
Cách khác: Nhận xét rằng y' chỉ đổi dấu khi x đi qua 7/2 nên hàm số chỉ có một cực trị
9 tháng 8 2023
\(y=x^8+\left(m-2\right)x^5-4\left(m^2-4\right)+1\)
Tập xác định \(D=ℝ\)
\(y'=8x^7+5\left(m-2\right)x^4\)
\(y''=56x^6+20\left(m-2\right)x^3\)
Để hàm số đạt cực tiểu tại \(x=0\)
\(\left\{{}\begin{matrix}y'\left(0\right)=0\\y''\left(0\right)>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}0m=0\\0m>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\forall m\inℝ\\m>0\end{matrix}\right.\) \(\Leftrightarrow m>0\)
Vậy \(m>0\) hàm số trên đạt cực tiểu tại \(x=0\)
TD
9 tháng 8 2023
Với đề thi THPT quốc gia môn Toán, đây là một trong những câu khó. Không nhiều các bạn học sinh giải được đề toán trên. Đây là một hàm số bậc 8, hoàn toàn khác với những hàm số thông dụng được học trên lớp, để giải được bài này, các bạn cần phải sử dụng kiến thức từ định nghĩa và tính chất của cực trị hàm số bất kì. Ta có:
y" = 8x7 + 5(m - 2)x4 - 4(m2 - 4)x3 + 1
Hàm đạt cực tiểu tại x = 0 thì y"(x) = 0 và y"(x) đổi dấu từ âm sang dương khi x chạy qua điểm 0. Từ đó ta tương đương với số hạng chứa x có lũy thừa thấp nhất có hệ số khác 0 trong biểu thức y’ là lũy thừa bậc lẻ, hệ số dương.
Có nghĩa là :
–4(m2 - 4) > 0 và m - 2 = m² – 4 = 0
⇔ –2 Bài 2 - Mã đề 124 đề thi môn Toán THPT Quốc gia 2017
Dưới đây là hàm số y = f(x) được thể hiện trong bình với bảng biến thiên:
Tìm giá trị cực tiểu, cực đại của hàm số đã cho.
Bài giải:
Theo như bảng biến thiên các em học sinh nhận thấy được cực tiểu là 0 và giá trị cực đại của hàm số là 3.
Nhiều câu hỏi cho sẵn bảng biến thiên hay hình vẽ đồ thị hàm số sẽ xuất hiện trong đề thi. Chúng ta có thể vận dụng chính những dữ liệu này để có cho mình được đáp án đúng một cách nhanh chóng.
Đây nhé bro:))!
AM
12 tháng 2 2022
Ta có: \(F\left(x\right)=\dfrac{1}{x}=\int x^2f\left(x\right)dx\)
Hay \(F'\left(x\right)=-\dfrac{1}{x^2}=x^2f\left(x\right)\Rightarrow f\left(x\right)=\dfrac{-1}{x^4}\)
Có: \(f'\left(x\right)=\dfrac{4}{x^3}\) \(\Rightarrow I=\int f'\left(x\right)x^3lnxdx=\int\dfrac{4}{x^3}x^3lnxdx=4\int lnxdx\)
Đặt: \(\left\{{}\begin{matrix}u=lnx\\dv=dx\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{1}{x}dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I=\text{4}(xlnx-\int x\dfrac{1}{x}dx)=4x\left(lnx-1\right)\)
PT
1
CM
6 tháng 10 2019
Đáp án B
Hàm số y = x + 1 3 (5 - x) xác định trên R.
y' = - x + 1 3 + 3 x + 1 2 (5 - x) = 2 x + 1 2 (7 - 2x)
y' = 0 ⇔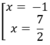 
Bảng biến thiên
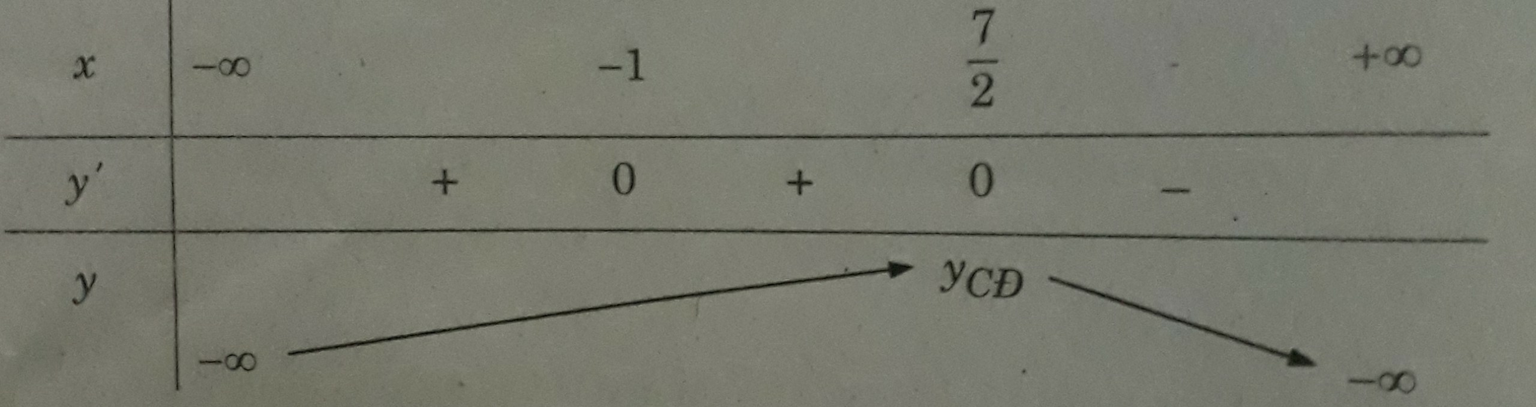
Suy ra hàm số chỉ có một cực trị (là cực đại)
Cách khác: Nhận xét rằng y' chỉ đổi dấu khi x đi qua 7/2 nên hàm số chỉ có một cực trị
A
0
SC
12 tháng 1 2022
Tuyệt vời, đợi mình load rồi mình hỏi thêm vào câu nữa nha bẹn
CM
23 tháng 8 2017
+ Ta có đạo hàm y’ = 3x2- 12x+ 3( m+ 2)
Phương trình y’ = 0 khi 3x2- 12x+ 3( m+ 2) = 0
+ Hàm số có 2 điểm cực trị x1; x2 ⇔ Δ’ > 0 ⇔ m < 2
+ Chia y cho y’ ta được :y= 1/3.y’( x-2) + (m-2) (2x+ 1)
Tọa độ 2 điểm cực trị tương ứng : A( x1 ; ( m-2) ( 2x1+ 1) ) và B( x2 ; ( m-2) ( 2x2+ 1) )
+ ta có ; y1.y2= ( m-2) 2( 4x1x2+ 2( x1+ x2) + 1)
Với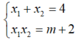 
nên: y1y2= ( m-2) 2( 4m+ 17)
Hai cực trị cùng dấu khi và chỉ khi y1.y2> 0 hay ( m-2) 2( 4m+ 17) > 0
⇔ m > - 17 4 m ≠ 2
Kết hợp điều kiện ta được : -17/4< m< 2; mà m nguyên nên m= -4; -3; ...0; 1
Có tất cả 6 giá trị nguyên của m thỏa mãn đầu bài.
Chọn C.
TL:
354 468 x 2758 x X = 46 284 x 32
354 468 x 2758 x X = 46 284 x 9
354 468 x 2758 x X = 416 556
2758 x X = 416 556 : 354 468
2758 x X = 1,17518265....
X = 1,17518265.. : 1758
X = 4,260907416x104
Ối dồi ôi, máy tính của e nó còn đau đầu
Cho số to thế
HT