
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a: Ta có: ΔOED cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)ED
Vì \(\widehat{OKA}=90^0\)(OK\(\perp\)ED)
nên K nằm trên đường tròn đường kính OA(1)
Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên OBAC là tứ giác nội tiếp đường tròn đường kính OA(2)
Từ (1) và (2) suy ra K,O,B,A,C cùng thuộc đường tròn đường kính OA
Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(3)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(4)
Từ (3) và (4) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC
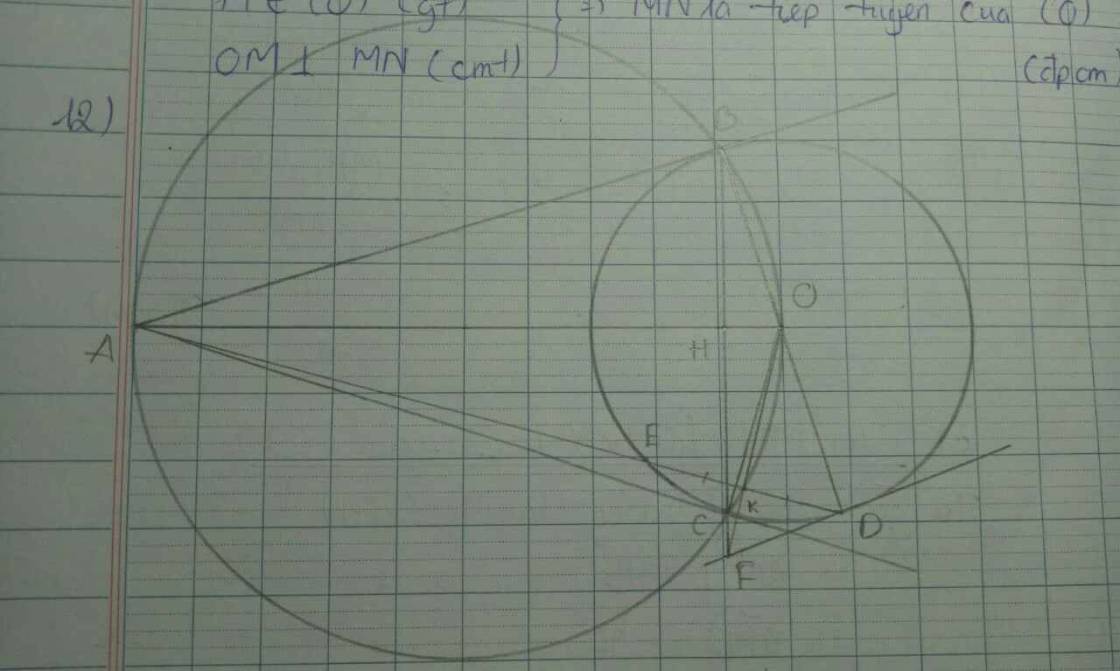
b: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
=>BE\(\perp\)ED tại E
=>BE\(\perp\)AD tại E
Xét ΔBAD vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\)
mà AB=AC
nên \(AE\cdot AD=AC^2\)
c: Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2=OD^2\left(5\right)\)
Xét ΔOHF vuông tại H và ΔOKA vuông tại K có
\(\widehat{HOF}\) chung
Do đó: ΔOHF đồng dạng với ΔOKA
=>\(\dfrac{OH}{OK}=\dfrac{OF}{OA}\)
=>\(OH\cdot OA=OK\cdot OF\left(6\right)\)
Từ (5) và (6) suy ra \(OK\cdot OF=OD^2\)
=>\(\dfrac{OK}{OD}=\dfrac{OD}{OF}\)
Xét ΔOKD và ΔODF có
\(\dfrac{OK}{OD}=\dfrac{OD}{OF}\)
\(\widehat{KOD}\) chung
Do đó: ΔOKD đồng dạng với ΔODF
=>\(\widehat{OKD}=\widehat{ODF}\)
mà \(\widehat{OKD}=90^0\)
nên \(\widehat{ODF}=90^0\)
=>FD là tiếp tuyến của (O)

1: góc AHC+góc AKC=180độ
=>AHCK nội tiếp
2: góc AHK=góc ACK=góc ABC
3: AH^2=AI*AK
=>AH^2=2*AM*2NA
mà AH=AM+AN
nên (AM-AN)^2=0
=>AM=AN
=>2AM=2AN
=>AP=AK
=>A nằm chính giữa cung BC
=>A,O,H thẳng hàng


b: Xét ΔMAN và ΔMPA có
góc MAN=góc MPA
góc AMN chung
=>ΔMAN đồng dạng với ΔMPA
=>MA/MP=MN/MA
=>MA^2=MN*MP

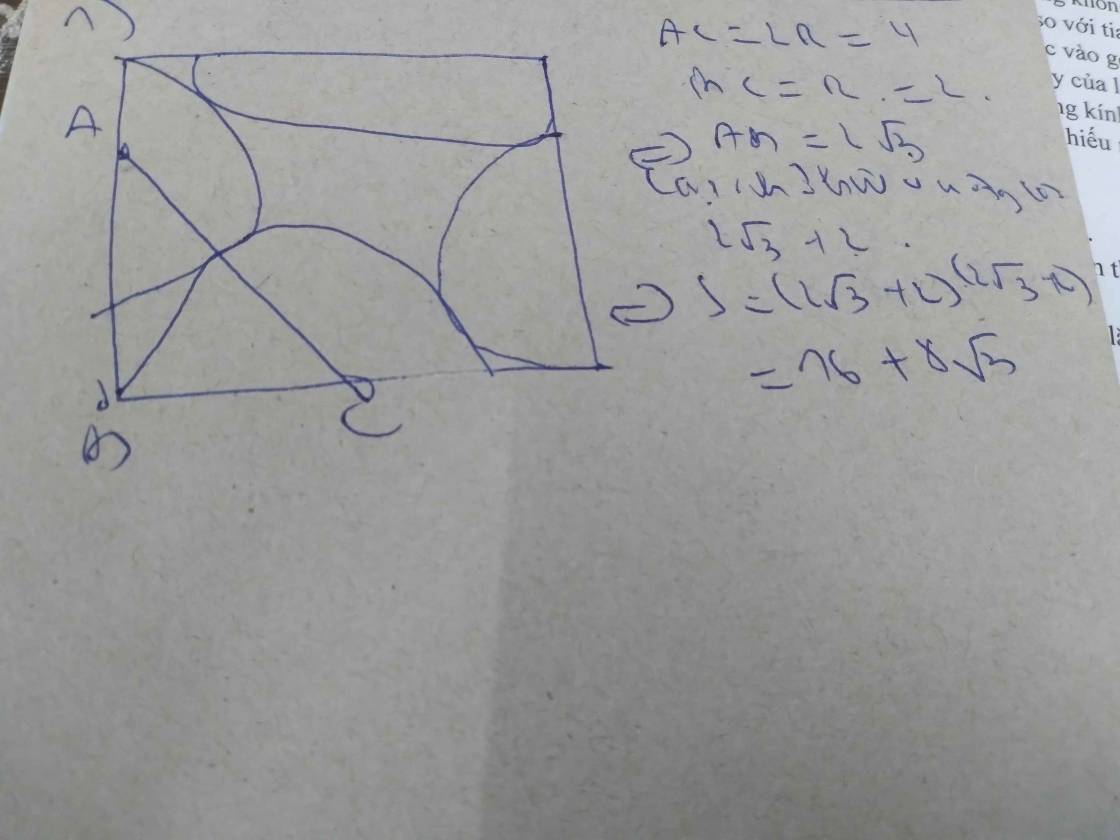
a. \(\dfrac{\sqrt{4-2\sqrt{3}}}{1-\sqrt{3}}=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{1-\sqrt{3}}=\dfrac{\sqrt{3}-1}{1-\sqrt{3}}=-1\)
b. \(\dfrac{3}{\sqrt{2}-1}-\dfrac{3}{\sqrt{2}+1}\)
\(=\dfrac{3\left(\sqrt{2}+1\right)}{2-1}-\dfrac{3\left(\sqrt{2}-1\right)}{2-1}\)
\(=3\sqrt{2}+3-3\sqrt{2}+3\)
\(=6\)

a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp










a) vì I là tâm đường tròn ngoại tiếp tứ giác BKHN
=> IB=IK=IH=IN
Xét tam giác BKH vuông tại K
có IB=IK=IH => IK là trung tuyến của BH => I là trung điểm của BH
tứ giác BKHN nt đường tròn tâm I đường kính BH