
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c: Ta có: \(\sqrt{x+4\sqrt{x-4}}=5\)
\(\Leftrightarrow\sqrt{x-4}+2=5\)
\(\Leftrightarrow\sqrt{x-4}=3\)
\(\Leftrightarrow x-4=9\)
hay x=13
c: Ta có: √x+4√x−4=5x+4x−4=5
⇔√x−4+2=5⇔x−4+2=5
⇔√x−4=3⇔x−4=3
⇔x−4=9⇔x−4=9
hay x=13

2.1
ĐKXĐ: \(x\ge-\dfrac{1}{16}\)
\(x^2-x-20-2\left(\sqrt{16x+1}-9\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4\right)-\dfrac{32\left(x-5\right)}{\sqrt{16x+1}+9}=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4-\dfrac{32}{\sqrt{16x+1}+9}\right)=0\) (1)
Do \(x\ge-\dfrac{1}{16}\Rightarrow\left\{{}\begin{matrix}\dfrac{32}{\sqrt{16x+1}+9}< \dfrac{32}{9}\\x+4\ge-\dfrac{1}{16}+4=\dfrac{63}{16}>\dfrac{32}{9}\end{matrix}\right.\)
\(\Rightarrow x+4-\dfrac{32}{\sqrt{16x+1}+9}>0\)
Nên (1) tương đương:
\(x-5=0\)
\(\Leftrightarrow x=5\)
Câu 2.2, 2.3 đề lỗi không dịch được

Bài 2:
Xét ΔABC vuông tại C có
\(CB=BA\cdot\sin60^0=12\cdot\dfrac{\sqrt{3}}{2}=6\sqrt{3}\left(cm\right)\)

Bài 8:
\(1,P=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ P=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\\ 2,P=2\Leftrightarrow2\sqrt{x}+4=3\sqrt{x}\Leftrightarrow\sqrt{x}=4\\ \Leftrightarrow x=16\left(tm\right)\)
Bài 9:
\(a,M=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ M=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\left(\sqrt{x}-1\right)\\ M=\dfrac{x-1}{\sqrt{x}}\\ b,M>0\Leftrightarrow x-1>0\left(\sqrt{x}>0\right)\\ \Leftrightarrow x>1\)
Bài 10:
\(a,A=\dfrac{\sqrt{\left(x+3\right)^2}}{x+3}=\dfrac{\left|x+3\right|}{x+3}\)
Với \(x\ge-3\Leftrightarrow A=\dfrac{x+3}{x+3}=1\)
Với \(x< -3\Leftrightarrow A=\dfrac{-\left(x+3\right)}{x+3}=-1\)
\(b,B=\dfrac{2}{x-1}\cdot\dfrac{\left|x-1\right|}{2\left|x\right|}\)
Với \(0< x< 1\Leftrightarrow B=\dfrac{2}{x-1}\cdot\dfrac{-\left(x-1\right)}{2x}=-\dfrac{1}{x}\)

\(13,=\dfrac{\sqrt{3}\left(\sqrt{6}-2\right)}{\sqrt{6}-2}+\dfrac{4\left(\sqrt{3}-1\right)}{2}+12-3\sqrt{3}\\ =\sqrt{3}+2\sqrt{3}-2+12-3\sqrt{3}=10\\ 14,=\dfrac{12\left(4+\sqrt{10}\right)}{6}-3\sqrt{10}+\dfrac{\sqrt{10}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}\\ =8+2\sqrt{10}-3\sqrt{10}+\sqrt{10}=8\\ 15,=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\\ =\dfrac{-3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{-3}{\sqrt{x}-3}\)
\(16,=\dfrac{x+2\sqrt{x}-3-x+3\sqrt{x}-4\sqrt{x}-6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ 17,=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)


Bài 14:
a)
Sửa đề: \(AE\cdot AB=AD\cdot AC\)
Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔADB\(\sim\)ΔAEC(g-g)
Suy ra: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
hay \(AE\cdot AB=AD\cdot AC\)(đpcm)
b) Ta có: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)(cmt)
nên \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét ΔADB vuông tại D có
\(\cos\widehat{A}=\dfrac{AD}{AB}\)
Xét ΔAED và ΔACB có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)(cmt)
\(\widehat{A}\) chung
Do đó: ΔAED∼ΔACB(c-g-c)
Suy ra: \(\dfrac{AD}{AB}=\dfrac{ED}{CB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AD}{AB}\cdot BC=DE\)
\(\Leftrightarrow DE=BC\cdot\cos\widehat{A}\)(đpcm)
c) Ta có: \(DE=BC\cdot\cos\widehat{A}\)(cmt)
nên \(DE=BC\cdot\cos60^0=\dfrac{1}{2}BC\)(1)
Ta có: ΔEBC vuông tại E(gt)
mà EM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(EM=\dfrac{1}{2}BC\)(2)
Ta có: ΔDBC vuông tại D(gt)
mà DM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(DM=\dfrac{1}{2}BC\)(3)
Từ (1), (2) và (3) suy ra ME=MD=DE
hay ΔMDE đều(đpcm)






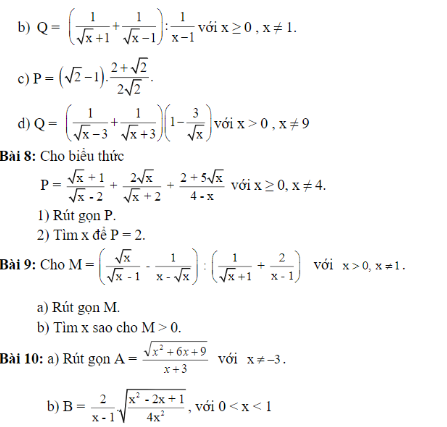




 Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ
Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ