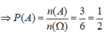Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xác suất:
a. \(\dfrac{3}{6}.\dfrac{3}{6}=\dfrac{1}{4}\)
b. \(\dfrac{6}{36}=\dfrac{1}{6}\)
c. Xác suất mặt 6 chấm ko xuất hiện lần nào: \(\dfrac{5}{6}.\dfrac{5}{6}=\dfrac{25}{36}\)
Xác suất mặt 6 xuất hiện ít nhất 1 lần: \(1-\dfrac{25}{36}=\dfrac{11}{36}\)
d. Các trường hợp tổng 2 mặt lớn hơn hoặc bằng 10: (6;4), (4;6); (5;5); (5;6);(6;5);(6;6) có 6 khả năng
\(\Rightarrow36-6=30\) khả năng tổng số chấm bé hơn 10
Xác suất: \(\dfrac{30}{36}=\dfrac{5}{6}\)
Đáp án A.
Số phần tử của không gian mẫu là 
Gọi A là biến cố thỏa yêu cầu bài toán.
Phương trình 
có nghiệm khi và chỉ khi
Xét bảng kết quả sau (L – loại, không thỏa; N – nhận, thỏa yêu cầu đề bài):
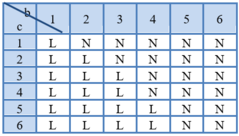
Dựa vào bảng kết quả trên ta thấy số kết quả thuận lợi cho A là 19.
Vậy xác suất của biến cố A là 
Chọn B
Gọi Ai : “lần gieo thứ i xuất hiện mặt 6 chấm.”, với 
⇒ 
⇒ 
A : “mặt có 6 chấm chỉ xuất hiện trong lần gieo thứ 3”
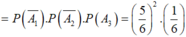
Đáp án A.
Tổng số chấm xuất hiện trong hai lần gieo lớn hơn hoặc bằng 11 khi các kết quả là (6;6), (5;6), (6;5)
Gọi x là xác suất xuất hiện mặt 6 chấm suy ra x 2 là xác suất xuất hiện các mặt còn lại.
Ta có: 5 x 2 + x = 1 ⇒ x = - 2 7
Do đó xác suất cần tìm là: 2 7 2 + 2 7 . 1 7 + 1 7 . 2 7 = 8 49 .
Rõ ràng \(\Omega=\left\{\left(i;j\right):1\le i,j\le6\right\}\)
Kí hiệu :
\(A_1:\) "Lần đầu xuất hiện mặt 1 chấm"
\(B_1:\) "Lần thứ hai xuất hiện mặt 1 chấm"
\(C:\) " Tổng số chấm là 6"
\(D:\) "Mặt 1 chấm xuất hiện ít nhất một lần"
a) Ta có \(C=\left\{\left(1,5\right),\left(5,1\right),\left(2,4\right),\left(4,2\right)\left(3,3\right)\right\},P\left(C\right)=\dfrac{5}{36}\)
b) Ta có \(A_1,B_1\) độc lập và \(D=A_1\cup B_1\) nên
\(P\left(D\right)=P\left(A_1\right)+P\left(B_1\right)-P\left(A_1B_1\right)\)
\(=\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{6}.\dfrac{1}{6}=\dfrac{11}{36}\)
Gọi Ai là biến cố:” xuất hiện mặt sáu chấm ở lần thứ i”, i=1,2,3 X là biến cố:” có ít nhất một lần xuất hiện mặt thứ 6” thì
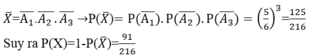
Chọn B
Đáp án là A.
• Số phần tử của không gian mẫu là n ( Ω ) = 36 .
Gọi A là biến cố thỏa yêu cầu bài toán.
Phương trình x2 + bx + c = 0 có nghiệm khi và chỉ khi ∆ = b 2 - 4 a c ≥ 0 ⇔ b 2 ≥ 4 a c .
Xét bảng kết quả (L – loại, không thỏa ; N – nhận, thỏa yêu cầu đề bài)
Chọn C
Số phần tử của không gian mẫu của phép thử gieo một con súc sắc hai lần liên tiếp là 36.
Để phương trình bậc hai
x
2
+ bx + c = 0 có nghiệm là 
(*) với 
Gọi A là biến cố chọn cặp số (b;c) thỏa mãn 
trong đó 
Khi c = 1: Các giá trị của b thỏa mãn điều kiện (*) là: 2,3,4,5,6. Suy ra có: 5 cặp (b,c).
Khi c = 2: Các giá trị của b thỏa mãn điều kiện (*) là: 3,4,5,6. Suy ra có: 4 cặp (b,c).
Khi c = 3: Các giá trị của b thỏa mãn điều kiện (*) là: 4,5,6. Suy ra có: 3 cặp (b,c).
Khi c = 4: Các giá trị của b thỏa mãn điều kiện (*) là: 4,5,6. Suy ra có: 3 cặp (b,c).
Khi c = 5: Các giá trị của b thỏa mãn điều kiện (*) là: 5,6. Suy ra có: 2 cặp (b,c).
Khi c = 6: Các giá trị của b thỏa mãn điều kiện (*) là: 5,6. Suy ra có: 2 cặp (b,c).
Vậy, số cặp (b,c) thỏa mãn điều kiện (*) là 19