Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Rõ ràng \(\Omega=\left\{\left(i;j\right):1\le i,j\le6\right\}\)
Kí hiệu :
\(A_1:\) "Lần đầu xuất hiện mặt 1 chấm"
\(B_1:\) "Lần thứ hai xuất hiện mặt 1 chấm"
\(C:\) " Tổng số chấm là 6"
\(D:\) "Mặt 1 chấm xuất hiện ít nhất một lần"
a) Ta có \(C=\left\{\left(1,5\right),\left(5,1\right),\left(2,4\right),\left(4,2\right)\left(3,3\right)\right\},P\left(C\right)=\dfrac{5}{36}\)
b) Ta có \(A_1,B_1\) độc lập và \(D=A_1\cup B_1\) nên
\(P\left(D\right)=P\left(A_1\right)+P\left(B_1\right)-P\left(A_1B_1\right)\)
\(=\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{6}.\dfrac{1}{6}=\dfrac{11}{36}\)

Xác suất:
a. \(\dfrac{3}{6}.\dfrac{3}{6}=\dfrac{1}{4}\)
b. \(\dfrac{6}{36}=\dfrac{1}{6}\)
c. Xác suất mặt 6 chấm ko xuất hiện lần nào: \(\dfrac{5}{6}.\dfrac{5}{6}=\dfrac{25}{36}\)
Xác suất mặt 6 xuất hiện ít nhất 1 lần: \(1-\dfrac{25}{36}=\dfrac{11}{36}\)
d. Các trường hợp tổng 2 mặt lớn hơn hoặc bằng 10: (6;4), (4;6); (5;5); (5;6);(6;5);(6;6) có 6 khả năng
\(\Rightarrow36-6=30\) khả năng tổng số chấm bé hơn 10
Xác suất: \(\dfrac{30}{36}=\dfrac{5}{6}\)

a. Có 3 mặt nguyên tố: 2,3,5 nên xác suất xuất hiện số nguyên tố ở mỗi lần gieo là \(\dfrac{3}{6}=\dfrac{1}{2}\)
Xác suất 2 lần đều xuất hiện số nguyên tố: \(\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{4}\)
b. Xác suất để lần 1 xuất hiện mặt 6 chấm: \(\dfrac{1}{6}\)
c. Xác suất ít nhất 1 lần xuất hiện mặt 6 chấm: \(\dfrac{2.6-1}{36}=\dfrac{11}{36}\)
d. Xác suất ko lần nào xuất hiện 6 chấm: \(1-\dfrac{11}{36}=\dfrac{25}{36}\)

Không gian mẫu là Ω = {1, 2, 3, 4, 5, 6}. Số kết quả có thế có thể có là 6 (hữu hạn); các kết quả đồng khả năng.
Ta có bảng:
|
b |
1 |
2 |
3 |
4 |
5 |
6 |
|
∆ = b2 - 8 |
-7 |
-4 |
1 |
8 |
17 |
28 |
a) Phương trình x2 + bx + 2 = 0 có nghiệm khi và chỉ khi ∆ = b2 - 8 ≥ 0 (*). Vì vậy nếu A là biến cố: "Xuất hiện mặt b chấm sao cho phương trình x2 + bx + 2 = 0 có nghiệm"
thì A = {3, 4, 5, 6}, n(A) = 4 và
P(A) = =
.
b) Biến cố B: "Xuất hiện mặt b chấm sao cho phương trình x2 + bx + 2 = 0 vô nghiệm" là biến cố A, do đó theo qui tắc cộng xác suất ta có
P(B) = 1 - P(A) = .
c) Nếu C là biến cố: "Xuất hiện mặt b chấm sao cho phương trình x2 + bx + 2 = 0 có nghiệm nguyên" thì C = {3}, vì vậy
P(C) = .

Không gian mẫu là kết quả của việc gieo 3 lần súc sắc
⇒ n(Ω) = 6.6.6 = 216.
A: “ Mặt 6 chấm xuất hiện ít nhất 1 lần”
⇒ A−: “ Không xuất hiện mặt 6 chấm”
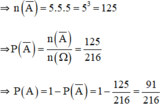


Gọi Ai là biến cố:” xuất hiện mặt sáu chấm ở lần thứ i”, i=1,2,3 X là biến cố:” có ít nhất một lần xuất hiện mặt thứ 6” thì
Chọn B