Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Ω = {S1, S2, S3, S4, S5, N1, N2, N3, N4, N5}
b)
A = {S2, S4, S6};
B = {N1, N3, N5}.

Biến cố M:”con súc sắc xuất hiện mặt chẵn chấm và đồng tiền xuất hiện mặt sấp” nên M={2S,4S,6S}.
Chọn đáp án là D

Đáp án C.
Ω = 1 S , 2 S , 2 S , 4 S , 5 S , 6 S , 1 N , 2 N , 3 N , 4 N , 5 N , 6 N

b) Biến cố A xảy ra khi mặt có số chấm không nhỏ hơn 2 xuất hiện
Vậy A={2,3,4,5,6}. Chọn phương án là C

a) Không gian mẫu có dạng
Ω = {SSS, SSN, SNS, NSS, SNN, NSN, NNS, NNN}
b)
A = {SSS, SNS, SSN, SNN};
B = {SSS, NNN};
C = {SSN, SNS, NSS};
D = {NN N } = Ω \ {NNN}.

Gọi B là biến cố: “Tổng số chấm xuất hiện trên bề mặt con súc sắc bằng 12”
Ta thấy
12 = 1 + 5 + 6 = 2 + 4 + 6 = 2 + 5 + 5 = 3 + 3 + 6 = 3 + 4 + 5 = 4 + 4 + 4
Nếu số chấm trên bề mặt 3 con súc sắc khác nhau tức là các trường hợp (1;5;6), (2;4;6), (3;4;5) có 3 ! .3 = 18 cách
Nếu số chấm trên bề mặt 3 con súc sắc có 2 con giống nhau tức là các trường hợp (2;5;5) và (3;3;6) có 3.2 = 6 cách
Nếu số chấm trên bề mặt 3 con súc sắc giống nhau ta có 1 cách gieo duy nhất
⇒ n B = 18 + 6 + 1 = 25 . Vậy P B = n B Ω B = 25 216 .
Chọn A

a. Không gian mẫu gồm 36 kết quả đồng khả năng xuất hiện, được mô tả như sau:
Ta có: Ω = {(i, j) | 1 ≤ i , j ≤ 6}, trong đó i, j lần lượt là số chấm xuất hiện trong lần gieo thứ nhất và thứ hai, n(Ω) = 36.
b. A = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)} ⇒ n(A) = 6
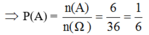
B = {(1, 5), (2, 5), (3, 5), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 5)}