K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 9 2019
\(\frac{2x-1}{3x^2+7x+2}+\frac{3}{9x^2+15x+4}-\frac{2x+7}{3x^2-5x-12}=\frac{5}{x+2}\)
\(\Leftrightarrow\frac{2x-1}{\left(3x+1\right)\left(x+2\right)}+\frac{3}{\left(3x+1\right)\left(3x+4\right)}-\frac{2x+7}{\left(4x+3\right)\left(x-3\right)}=\frac{5}{\left(x+2\right)}\)
\(\Leftrightarrow\frac{1}{x+2}-\frac{1}{3x+1}+\frac{1}{3x+1}-\frac{1}{3x+4}+\frac{1}{3x+4}-\frac{1}{x-3}=\frac{5}{x+2}\)
\(\Leftrightarrow\frac{1}{x+2}-\frac{1}{x-3}=\frac{5}{x+2}\)
\(\Leftrightarrow\frac{x-3-x-2}{\left(x+2\right)\left(x-3\right)}=\frac{5\left(x-3\right)}{\left(x+2\right)\left(x-3\right)}\)
\(\Leftrightarrow5x-3=-5\)
\(\Leftrightarrow x=-\frac{2}{5}\)
Chúc bạn học tốt !!!
15 tháng 1 2017
Bài 1:
Đặt \(t=2x^2+3x-1\) ta có:
\(t^2-5\left(t+4\right)+24=0\)
\(\Rightarrow t^2-5t-20+24=0\)
\(\Rightarrow t^2-5t+4=0\)
\(\Rightarrow\left(t-4\right)\left(t-1\right)=0\)\(\Rightarrow\left[\begin{matrix}t=4\\t=1\end{matrix}\right.\)
*)Xét \(2x^2+3x-1=4\)
\(\Rightarrow\left(x-1\right)\left(2x+5\right)=0\)\(\Rightarrow\left[\begin{matrix}x=1\\x=-\frac{5}{2}\end{matrix}\right.\)
*)Xét \(2x^2+3x-1=1\)
\(\Rightarrow\left(x+2\right)\left(2x-1\right)=0\)\(\Rightarrow\left[\begin{matrix}x=-2\\x=\frac{1}{2}\end{matrix}\right.\)
15 tháng 1 2017
Bài 2:
\(\left(x^2-4\right)\left(x+3\right)=\left(x^2-4\right)\left(x-1\right)\)
\(\Rightarrow\left(x^2-4\right)\left(x+3\right)-\left(x^2-4\right)\left(x-1\right)=0\)
\(\Rightarrow\left(x^2-4\right)\left[x+3-\left(x-1\right)\right]=0\)
\(\Rightarrow4\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left(x-2\right)\left(x+2\right)=0\)\(\Rightarrow\left[\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
6 tháng 1 2019
\(x^4-3x^3+4x^2-3x-1=0\)
\(\Leftrightarrow x^4+x^3+2x^3+2x^2+2x^2+2x+x+1=0\)
\(\Leftrightarrow x^3\left(x+1\right)+2x^2\left(x+1\right)+2x\left(x+1\right)+\left(x+1\right)=0\)
\(\Leftrightarrow\left(x^3+2x^2+2x+1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x^3+2x^2+2x+1\right)\left(x+1\right)=0\)
\(\Leftrightarrow(x^3+x^2+x^2+x+x+1)\left(x+1\right)=0\)
\(\Leftrightarrow[x^2\left(x+1\right)+x\left(x+1\right)+\left(x+1\right)]\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+x+1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2\left(x^2+x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}(x+1)^2=0\\x^2+x+1=0\end{cases}}\Rightarrow\hept{\begin{cases}x+1=0\\\varnothing\end{cases}}\Rightarrow x=-1\)
KK
8 tháng 4 2020
Bây giờ a giải đc hệ này chưa ạ? Nếu giải đc r cho e xin lời giải đc ko ạ
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 9 2020
a/ \(=x^4+2x^3+2x^2+\left(x^3+2x^2+2x\right)-\left(5x^2+10x+10\right)\)
\(=x^2\left(x^2+2x+2\right)+x\left(x^2+2x+2\right)-5\left(x^2+2x+2\right)\)
\(=\left(x^2+x-5\right)\left(x^2+2x+2\right)\)
b/ \(=3x^4+x^3-x^2+\left(9x^3+3x^2-3x\right)-\left(18x^2+6x-6\right)\)
\(=x^2\left(3x^2+x-1\right)+3x\left(3x^2+x-1\right)-6\left(3x^2+x-1\right)\)
\(=\left(x^2+3x-6\right)\left(3x^2+x-1\right)\)
c/ Bạn xem lại đề, câu này ko phân tích được
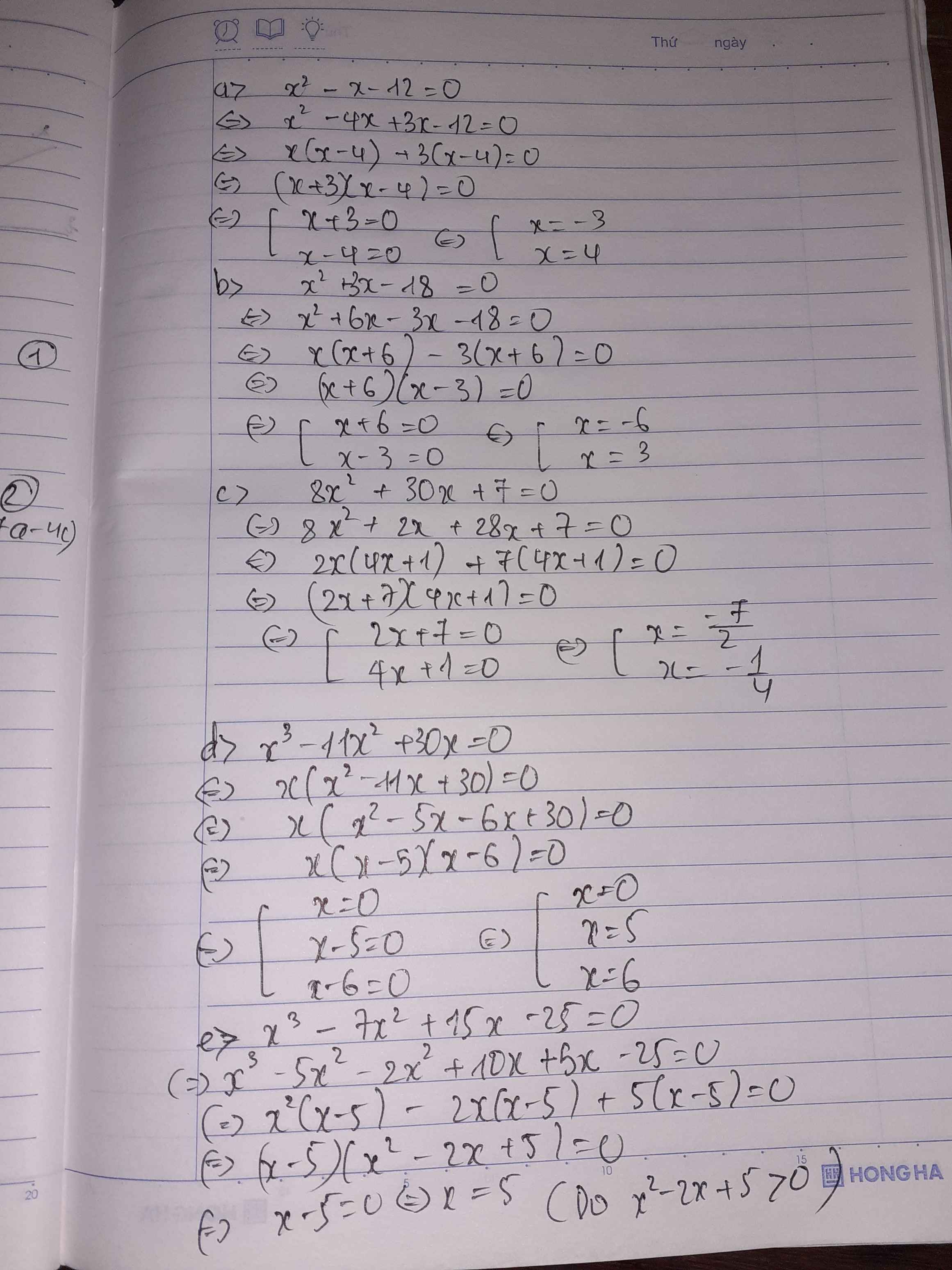
Phương trình phải có vế phải bạn nhé!