Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Kết quả 1: Chọn 2 nhóm: A và B rồi sắp xếp thứ tự “ A trình bày trước, B trình bày sau” hoặc “ B trình bày trước, A trình bày sau”.
- Kết quả 2: Chọn 2 nhóm: A và C rồi sắp xếp thứ tự “ A trình bày trước, C trình bày sau” hoặc “ C trình bày trước, A trình bày sau”.
- Kết quả 3: Chọn 2 nhóm: A và D rồi sắp xếp thứ tự “ A trình bày trước, D trình bày sau” hoặc “ D trình bày trước, A trình bày sau”.
- Kết quả 4: Chọn 2 nhóm: B trình bày và C trình bày rồi sắp xếp thứ tự “ B trình bày trước, C trình bày sau” hoặc “ C trình bày trước, B trình bày sau”.

Tổng số khả năng có thể xảy ra của phép thử là \(n\left( \Omega \right) = C_{12}^4\)
a) Số kết quả thuận lợi cho biến cố “Bốn bạn thuộc 4 tổ khác nhau” là số cách sắp xếp 4 bạn vào 4 tổ có \(4!\) cách
Vậy xác suất của biến cố “Bốn bạn thuộc 4 tổ khác nhau” là \(P = \frac{{4!}}{{C_{12}^4}} = \frac{8}{{165}}\)
b) Gọi A là biến cố “Bốn bạn thuộc 2 tổ khác nhau”
A xảy ra với 2 trường hợp sau:
TH1: 3 bạn cùng thuộc 1 tổ và 1 bạn thuộc tổ khác có \(C_4^3.C_3^1.C_2^1 = 24\) cách
TH2: cứ 2 bạn cùng thuộc 1 tổ \(C_4^2.C_3^1.C_2^2.C_2^1 = 36\) cách
Suy ra, số kết quả thuận lợi cho biến cố A là \(n\left( A \right) = 24 + 36 = 60\)
Vậy xác suất của biến cố “Bốn bạn thuộc 2 tổ khác nhau” là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{60}}{{C_{12}^4}} = \frac{4}{{33}}\)

a, Có 5 cách chọn nhóm trình bày thứ nhất.
b, Sau khi đã chọn nhóm trình bày thứ nhất, có 4 cách để chọn nhóm trình bày thứ hai.
c, Sau khi đã chọn 2 nhóm trình bày thứ nhất và thứ hai, có 3 cách để chọn nhóm trình bày thứ ba.
d, Theo quy tắc nhân, ta có số chỉnh hợp được tạo ra là: \(5.4.3 = 60\)

a, Có 3 cách để chọn nhóm trình bày thứ nhất.
b, Sau khi đã chọn nhóm trình bày thứ nhất thì còn lại 2 nhóm, vì vậy có 2 cách để chọn nhóm trình bày thứ 2.
c, Sau khi đã chọn nhóm trình bày thứ nhất và thứ hai thì còn lại một nhóm duy nhất nên ta có 1 cách chọn nhóm trình bày thứ 3.
d, Áp dụng quy tắc nhân, số hoán vị được tạo ra là: 3.2.1 = 6 (hoán vị).

a. \(C^1_7=7\left(cách\right)\)
b. \(C^1_3=3\left(cách\right)\)
c. Số cách không ra bạn nữ là chỉ chọn nam, vậy số cách chọn ít nhất 1 nữ là: \(7-3=4\left(cách\right)\)

Không gian mẫu: \(C_{10}^3\)
Số cách chọn sao cho có 2 nữ 1 nam là: \(C_6^2.C_4^1\)
Xác suất: \(P=\dfrac{C_6^2.C_4^1}{C_{10}^3}=\dfrac{1}{2}\)

a) Bước 1: Chọn 1 bạn từ 4 bạn trên: có 4 cách
Bước 2: Chọn 1 bạn từ 3 bạn còn lại
Do hai bạn có vai trò như nhau nên ta chia kết quả cho 2 để loại trường hợp trùng.
Có 4.2: 2 = 6 cách chọn hai bạn từ 4 bạn trên.
b) Chọn nhóm trưởng: có 4 cách
Chọn nhóm phó: có 3 cách
Theo quy tắc nhân , có 4.3 = 12 cách chọn hai bạn, trong đó một bạn làm nhóm trường, một bạn làm nhóm phó.

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II sản xuất ra.
Như vậy tiền lãi có được là L = 3x + 5y (nghìn đồng).
Theo đề bài: Nhóm A cần 2x + 2y máy;
Nhóm B cần 0x + 2y máy;
Nhóm C cần 2x + 4y máy;
Vì số máy tối đa ở nhóm A là 10 máy, nhóm B là 4 máy, nhóm C là 12 máy nên x, y phải thỏa mãn hệ bất phương trình: 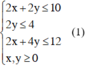
Khi đó bài toán trở thành: trong các nghiệm của hệ bất phương trình (1) thì nghiệm (x = xo; y = yo) nào cho L = 3x + 5y lớn nhất.
Miền nghiệm của hệ bất phương trình (1) là ngũ giác ABCDE kể cả miền trong.
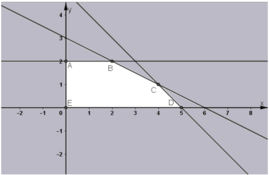
Ta có: L đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác ABCDE.
Tính giá trị của biểu thức L = 3x + 5y tại các đỉnh ta được:
Tại đỉnh A(0;2), L = 10
Tại đỉnh B(2; 2), L = 16
Tại đỉnh C(4; 1), L = 17
Tại đỉnh D(5; 0), L = 15
Tại đỉnh E(0; 0), L = 0.
Do đó, L = 3x + 5y lớn nhất là 17 (nghìn đồng) khi: x = 4; y = 1
Vậy để có tiền lãi cao nhất, cần sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm loại II.

Nhóm T có x 3 ≈ 163(cm); s 3 2 ≈ 169 ; s 3 ≈ 13
Học sinh ở nhóm nam và nhóm T có chiều cao như nhau và cùng lớn hơn chiều cao của học sinh ở nhóm nữ (vì x 1 = x 3 > x 2 )
Vì x 1 = x 3 = 163(cm) và s 1 < s 2 nên chiều cao của các học sinh nam đồng đều hơn chiều cao của các học sinh nhóm T.
Có \(C_{10}^2\) cách chọn 2 nhóm bất kì (không gian mẫu)
Có 2 biến cố thuận lợi: 1,2 hoặc 3,4
Do đó xác suất là: \(P=\dfrac{2}{C_{10}^2}\)
Ngồi học em nghĩ ra cái đề này anh ạ!