Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

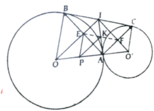
a, Chứng minh tứ giác AEIF là hình chữ nhật và K là trung điểm AI
b, Có IE.IO = I B 2 = B C 2 4 và IF.IO' = I C 2 = B C 2 4
=> 2.(IE.IO+IF.IO') = A B 2 + A C 2
c, PK Là đường trung bình của ∆OAI và là trung trực của EA
Ta có ∆PEK = ∆PAK nên P E K ^ = P A K ^
Vậy P E K ^ = 90 0 => đpcm
d, ∆ABC:∆IOO’ => S A B C S I O O ' = B C O O ' 2 => S A B C = S I O O ' . B C 2 O O ' 2
mà BC = 2AI'; OO' = 2a; S O I O ' = 1 2 . 2 a . I A = a . I A => S A B C = I A 2 a
I A 2 = R R ' ⩽ R + R ' 2 2 = a 2 => IA lớn nhất bằng a khi R=R’

https://diendantoanhoc.net/index.php?app=core&module=attach§ion=attach&attach_id=20602
Vào link này xem nhé
Học tốt!!!!!!!

Hình vẽ (Vào link là ra): https://i.imgur.com/GssTwiW.png
Ở đây mình sẽ cho R là bán kính của đường tròn O; R' là bán kính của đường tròn O'
a) ta có: \(\hept{\begin{cases}OM\perp MN\\O'N\perp MN\end{cases}}\)=> OM//O'N => \(\widehat{AOM}+\widehat{AO'N}=180^o\)
Xét ΔOAM có OM = OA (= R) => ΔOAM cân => \(\widehat{A_1}=\frac{180^o-\widehat{AOM}}{2}\left(1\right)\)
Xét ΔO'NA có O'N = O'A (=R') => ΔO'NA cân => \(\widehat{A_2}=\frac{180^o-\widehat{AO'N}}{2}\left(2\right)\)
\(\left(1\right)+\left(2\right)\Leftrightarrow\widehat{A_1}+\widehat{A_2}=\frac{180^o-\widehat{AOM}}{2}+\frac{180^o-\widehat{AO'N}}{2}.\)
\(=\frac{360^o-\left(\widehat{AOM}+\widehat{AO'N}\right)}{2}\)
\(=\frac{360^o-180^o}{2}=90^o.\)
\(\widehat{MAN}=180^o-\left(\widehat{A_1}+\widehat{A_2}\right)=180^o-90^o=90^o\)
=> ΔAMN vuông tại A
b) ta có: IM, IA là các tiếp tuyến của đường tròn (O) => IO là tia phân giác của \(\widehat{AIM}\)
IN; IA là các tiếp tuyến của đường tròn (O') => IO' là tia phân giác của \(\widehat{AIN}\)
do IO và IO' là hai tia phân giác của hai góc kề bù => \(IO\perp IO'\Rightarrow\widehat{OIO'}=90^o\)=> ΔIOO' là tam giác vuông.
c) Áp dụng hệ thức lượng trong ΔIOO', ta có: AI2 = OA . O'A = 8 x 4,5 = 36 => AI = 6(cm)
Xét ΔAMN vuông tại A, ta có: MN = 2AI = 2 x 6 = 12 (cm)
Đây là cách làm cùa mình. Nếu sai sót thì bình luận nhé!
Học tốt ^3^

Bài 2:
a: Xét (O) có
CM,CA là tiếp tuyến
nên OC là phân giác của góc MOA(1) và CM=CA
Xet (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
b:
Xét ΔCOD vuông tại O có OM là đường cao
nên MC*MD=OM^2
c: \(AC=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)