YC
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
Bài 1: Giải và biện luận các phương trình sau theo tham số m a) 2mx + 3 = m - x b) m(x - 2) = 3x + 1
1
6 tháng 12 2021
b: Để phương trình vô nghiệm thì x-2=0
hay x=2
Để phương trình có nghiệm thì x-2<>0
hay x<>2
PT
1
CM
29 tháng 11 2019
Phương trình đã cho tương đương với phương trình
(m - 1)(m + 3)x = 4(m - 1)
Với m ≠ 1 và m ≠ -3 phương trình có nghiệm 
Với m = 1 mọi số thực x đều là nghiệm của phương trình;
Với m = -3 phương trình vô nghiệm.
PT
1
CM
28 tháng 5 2018
Với 
phương trình đã cho trở thành
3x + 2m = x - m ⇔ 2x = -3m ⇔ x = -3m / 2
Ta có:
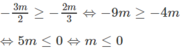
Với 
Phương trình đã cho trở thành
-3x - 2m = x - m ⇔ 4x = -m ⇔ x = -m / 4
Ta có:
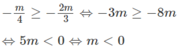
Kết luận
Với m > 0 phương trình vô nghiệm;
Với m = 0 phương trình có nghiệm x = 0;
Với m < 0 phương trình có nghiệm
PT
1
CM
8 tháng 2 2019
Phương trình (1) ⇔ x = -3m + 2
Phương trình (2) ⇔ 3x = m - 2 ⇔ x = (m - 2) / 3
Vậy với mọi giá trị của m phương trình có nghiệm là:
x 1 = -3m + 2 và x 2 = (m - 2) / 3
PT
1
CM
21 tháng 9 2017
m(x – 2) = 3x + 1
⇔ mx – 2m = 3x + 1
⇔ mx – 3x = 1 + 2m
⇔ (m – 3).x = 1 + 2m (1)
+ Xét m – 3 ≠ 0 ⇔ m ≠ 3, phương trình (1) có nghiệm duy nhất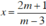 
+ Xét m – 3 = 0 ⇔ m = 3, pt (1) ⇔ 0x = 7. Phương trình vô nghiệm.
Kết luận:
+ với m = 3, phương trình vô nghiệm
+ với m ≠ 3, phương trình có nghiệm duy nhất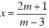 
CM
23 tháng 1 2017
m = 0 phương trình trở thành
-x - 2 = 0 ⇒ x = -2
m ≠ 0 phương trình đã cho là phương trình bậc hai, có Δ = 4m + 1
Với m < -1/4 phương trình vô nghiệm;
Với m ≥ -1/4 nghiệm của phương trình là
PT
1
CM
22 tháng 8 2019
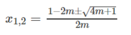
(2m + 1)x – 2m = 3x – 2
⇔ (2m + 1)x – 3x = 2m – 2
⇔ (2m + 1 – 3).x = 2m – 2
⇔ (2m – 2).x = 2m – 2 (3)
+ Xét 2m – 2 ≠ 0 ⇔ m ≠ 1, pt (3) có nghiệm duy nhất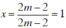 
+ Xét 2m – 2 = 0 ⇔ m = 1, pt (3) ⇔ 0.x = 0, phương trình có vô số nghiệm.
Kết luận :
+ Với m = 1, phương trình có vô số nghiệm
+ Với m ≠ 1, phương trình có nghiệm duy nhất x = 1.
PT
1
CM
11 tháng 11 2017
Điều kiện của phương trình là x ≠ -1, ta có
⇒ (m - 2)x + 3 = (2m - 1)(x + 1)
⇒ (m + 1)x = 4 - 2m (1)
Với m = -1 phương trình (1) vô nghiệm nên phương trình đã cho cũng vô nghiệm.
Với m ≠ -1 phương tình (1) có nghiệm 
Nghiệm này thỏa mãn điều kiện x ≠ -1 khi và chỉ khi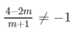 
hay -2m + 4 ≠ -m - 1 ⇒ m ≠ 5
Kết luận
Với m = -1 hoặc m = 5 phương trình vô nghiệm
Với m ≠ -1 và m ≠ 5 phương trình có nghiệm là 
PT
1
CM
8 tháng 9 2017
Điều kiện của phương trình là: x ≠ 3. Ta có:
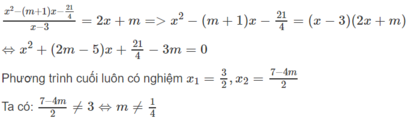
Kết luận
Với m ≠ 1/4 phương trình đã cho có hai nghiệm và x = 3/2 và x = (7 - 4m)/2
Với m ≠ 1/4 phương trình có một nghiệm x = 3/2
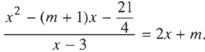
\(2mx+3=m-x\)
\(\Leftrightarrow x\left(2m+1\right)=m-3\)
+) Nếu \(2m+1=0\) và \(m-3=0\) thì phương trình nghiệm đúng \(\forall x\)
Khi đó \(m=-\frac{1}{2}\) và \(m=3\) (vô lí)
+) Nếu \(2m+1=0\) và \(m-3\ne0\) thì phương trình vô nghiệm
Khi đó:\(m=-\frac{1}{2}\) và \(m\ne3\) (chọn) +) Nếu \(2m+1\ne0\) và \(m-3\ne0\) thì phương trình có nghiệm duy nhất \(x=\frac{m-3}{2m+1}\) Khi đó \(m\ne3\) và \(m\ne-\frac{1}{2}\)