Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Để xác định được các sai số này, chúng ta cần tính được các sai số hệ thống và sai số ngẫu nhiên, tính toán các sai số.
- Nguyên nhân gây ra sai số có thể do nguyên nhân khách quan (do dụng cụ, điều kiện thực hành, thời tiết, nhiệt độ, độ ẩm), nguyên nhân chủ quan (thao tác đo chưa chính xác) hoặc có thể do dụng cụ ban đầu đã có sai số (sai số hệ thống).
- Cách khắc phục: thao tác đúng cách, lựa chọn thiết bị phù hợp, tiến hành đo nhiều lần.

- Các loại đơn vị đo:
+ Đơn vị đo độ dài: m, km, cm, …
+ Đơn vị đo vận tốc, tốc độ: m/s, km/h, …
+ Đơn vị đo thời gian: giây, giờ, phút, …
+ Đơn vị đo lực: Niuton (N)
…
- Các loại sai số có thể gặp:
+ Sai số ngẫu nhiên
+ Sai số hệ thống
- Cách hạn chế các loại sai số:
+ Khắc phục sai số ngẫu nhiên: thực hiện nhiều lần đo, lấy giá trị trung bình để hạn chế sự phân tán của số liệu đo.
+ Khắc phục sai số hệ thống: thường xuyên hiệu chỉnh dụng cụ đo, sử dụng thiết bị đo có độ chính xác cao.

1. Tính giá trị trung bình và sai số tuyệt đối của phép đo gia tốc rơi tự do
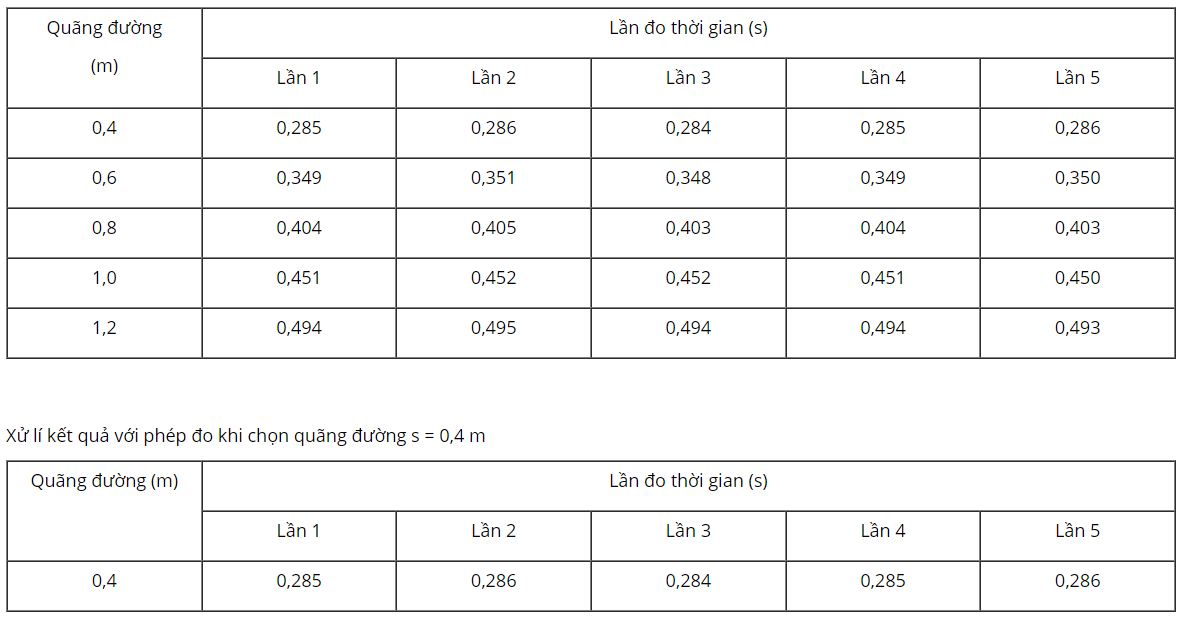
- Lần 1: \({g_1} = \frac{{2{s_1}}}{{t_1^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)
- Lần 2: \({g_2} = \frac{{2{s_2}}}{{t_2^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)
- Lần 3: \({g_3} = \frac{{2{s_3}}}{{t_3^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,919(m/{s^2})\)
- Lần 4: \({g_4} = \frac{{2{s_4}}}{{t_4^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)
- Lần 5: \({g_5} = \frac{{2{s_5}}}{{t_5^2}} = \frac{{2.0,4}}{{0,{{286}^2}}} = 9,780(m/{s^2})\)
Gia tốc trung bình là: \(\overline g = \frac{{9,849 + 9,849 + 9,919 + 9,849 + 9,780}}{5} = 9,849(m/{s^2})\)
Sai số tuyệt đối của gia tốc trong các lần đo
\(\begin{array}{l}\Delta {g_1} = \left| {\overline g - {g_1}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_2} = \left| {\overline g - {g_2}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_3} = \left| {\overline g - {g_3}} \right| = \left| {9,849 - 9,919} \right| = 0,07\\\Delta {g_4} = \left| {\overline g - {g_4}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_5} = \left| {\overline g - {g_5}} \right| = \left| {9,849 - 9,780} \right| = 0,069\end{array}\)
Sai số tuyệt đối trung bình là: \(\overline {\Delta g} = \frac{{\Delta {g_1} + \Delta {g_2} + \Delta {g_3} + \Delta {g_4} + \Delta {g_5}}}{5} = 0,028\)
Suy ra kết quả: \(g = 9,849 \pm 0,028\)
2. Trong thí nghiệm người ta dùng trụ thép làm vật rơi nhằm mục đích khi ta thả vật rơi thì xác suất phương rơi của vật chắn tia hồng ngoại ở cổng quang điện cao, giúp ta thực hiện thí nghiệm dễ dàng hơn
- Có thể dùng vật thả rơi là viên bi thép, nhưng xác suất khi thả rơi viên bi có phương rơi không chắn được tia hồng ngoại cao hơn khi dùng trụ thép, nên khi làm thí nghiệm với viên bi ta cần căn chỉnh và thả theo đúng phương của dây rọi.

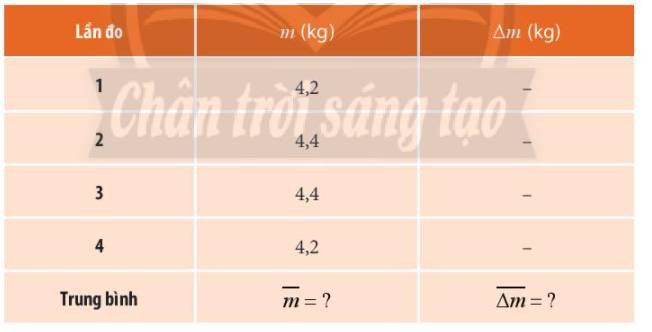
Giá trị trung bình khối lượng của túi trái cây là:
\(\overline m = \frac{{{m_1} + {m_2} + {m_3} + {m_4}}}{4} = \frac{{4,2 + 4,4 + 4,4 + 4,2}}{4} = 4,3(kg)\)
Sai số tuyệt đối ứng với mỗi lần đo là:
\(\begin{array}{l}\Delta {m_1} = \left| {\overline m - {m_1}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\\\Delta {m_2} = \left| {\overline m - {m_2}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_3} = \left| {\overline m - {m_3}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_4} = \left| {\overline m - {m_4}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\end{array}\)
Sai số tuyệt đối trung bình của phép đo:
\(\overline {\Delta m} = \frac{{\Delta {m_1} + \Delta {m_2} + \Delta {m_3} + \Delta {m_4}}}{4} = \frac{{0,1 + 0,1 + 0,1 + 0,1}}{4} = 0,1(kg)\)
Sai số tuyệt đối của phép đo là:
\(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = 0,1 + 0,1 = 0,2(kg)\)
Sai số tương đối của phép đo là:
\(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = \frac{{0,2}}{{4,2}}.100\% = 4,65\% \)
Kết quả phép đo:
\(m = \overline m \pm \Delta m = 4,3 \pm 0,2(kg)\)

a. Sai số tuyệt đối và sai số tỷ đối:
Ta tính tổng độ sai số của các giá trị đo lượng thực như sau:
Sai sốĐộ sai số
| 0 | 200mm |
| 0 | 200mm |
| 1 | 199mm |
| 5 | 200,05mm |
| 1 | 199,05mm |
Tổng độ sai số = 0 + 0 + 1 + 5 + 1 = 7
Giá trị thực là 550mm, vậy sai số tuyệt đối = |550 - 500| = 100.
Tỷ đối sai số = (7/1000) x 100 = 0.7%.
b. Kết quả phép đo:
Sai số tuyệt đối: 100mmSai số tỷ đối: 0.7%Vậy kết quả phép đo của chiều dài quyển sổ là 550mm với sai số tuyệt đối là 100mm và sai số tỷ đối là 0.7%.

a. Sai số tuyệt đối (MAD) và sai số tỷ đối (MAPE) được tính như sau:
Phép đo thực tế (TTT): 200,1mm, 200mm, 199mm, 200,05mm, 199,05mm
Phép đo lý thuyết (TDT): 200mm, 200mm, 200mm, 200mm, 200mm, 200mm
MAD = |(TTT - TDT)| = |(200,1 - 200), (200 - 200), (199 - 200), (200,05 - 200), (199,05 - 200)| = (0,1), 0, 1, 0, 1, 1 mm
MAPE = |(TTT - TDT)/TTT)|*100 = |(200,1 - 200)/200,1), (200 - 200)/200), (199 - 200)/199), (200,05 - 200)/200,05), (199,05 - 200)/199,05)|*100 = 0,05%, 0%, 0,05%, 0,05%, 0,05%
b. Kết quả phép đo:
Độ lỗi tuyệt đối tối đa: 1,1 mm (từ 0,1 mm tới 1,1 mm)Độ lỗi tỷ đối tối đa: 0,05% (từ 0% tới 0,05%)Vậy độ lỗi tuyệt đối và tỷ đối tối đa của phép đo đo chiều dài quyển sách 5 lần là:
Độ lỗi tuyệt đối tối đa: 1,1 mmĐộ lỗi tỷ đối tối đa: 0,05%


Để đo một đại lượng chính xác người ta cần lặp lại phép đo nhiều lần để làm giảm sai số ngẫu nhiên đến mức nhỏ nhất và tính sai số để xác định được độ tin cậy của phép đo.