Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Góc ở tâm có số đo bằng hai lần số đo cung bị chắn nên góc AOB sẽ có số đo là 120 độ. ( Gấp hai lần góc C á)

tại vì cái này sẽ suy ra được là kiểu nó có góc bằng một nửa số đo cung bị chắn mà không phải là góc nội tiếp thì là góc tạo bởi tiếp tuyến và dây cung á bạn
=>OF là tiếp tuyến
P/S: Cái này là theo mình suy nghĩ thôi nha, chứ mình cũng không chắc á

Ta có hình vẽ sau:
Vì góc nội tiếp \(\widehat{BAC}\) chắn \(\stackrel\frown{BC}\) nên \(sđ\stackrel\frown{BC}=2\cdot sđ\widehat{BAC}=2\cdot30^o=60^o\)
Vì B,C ∈ (O;R) và nên \(\left[{}\begin{matrix}OB=OC\\\widehat{BOC}=60^o\end{matrix}\right.\)
Xét ▲OBC có: \(OB=OC\)
\(\widehat{BOC}=60^o\)
⇔▲OBC đều
➤\(\widehat{CBO}=60^o\)

Bạn tự vẽ hình :)
a) Ta có : AB = Cos 60 . BC = 1/2 . 12 = 6 cm
AC = Sin 60 . BC = \(\frac{\sqrt{3}}{2}.12=6\sqrt{3}\)
b) BE là tia p/g góc B nên ta có góc ABE = góc EBC = 30 độ
AE = tan 30 . AB = ...
BH = Cos 60. AB = ....
Suy ra AE . AC =BH.BC (bạn tự thay số vào tính)
c) Hãy chứng minh D là trung điểm AH
Sau đó áp dụng tính chất đường trung bình để suy ra DM , DN , MN song song với BC và áp dụng tiên đề Ơ-Clit là ra :)

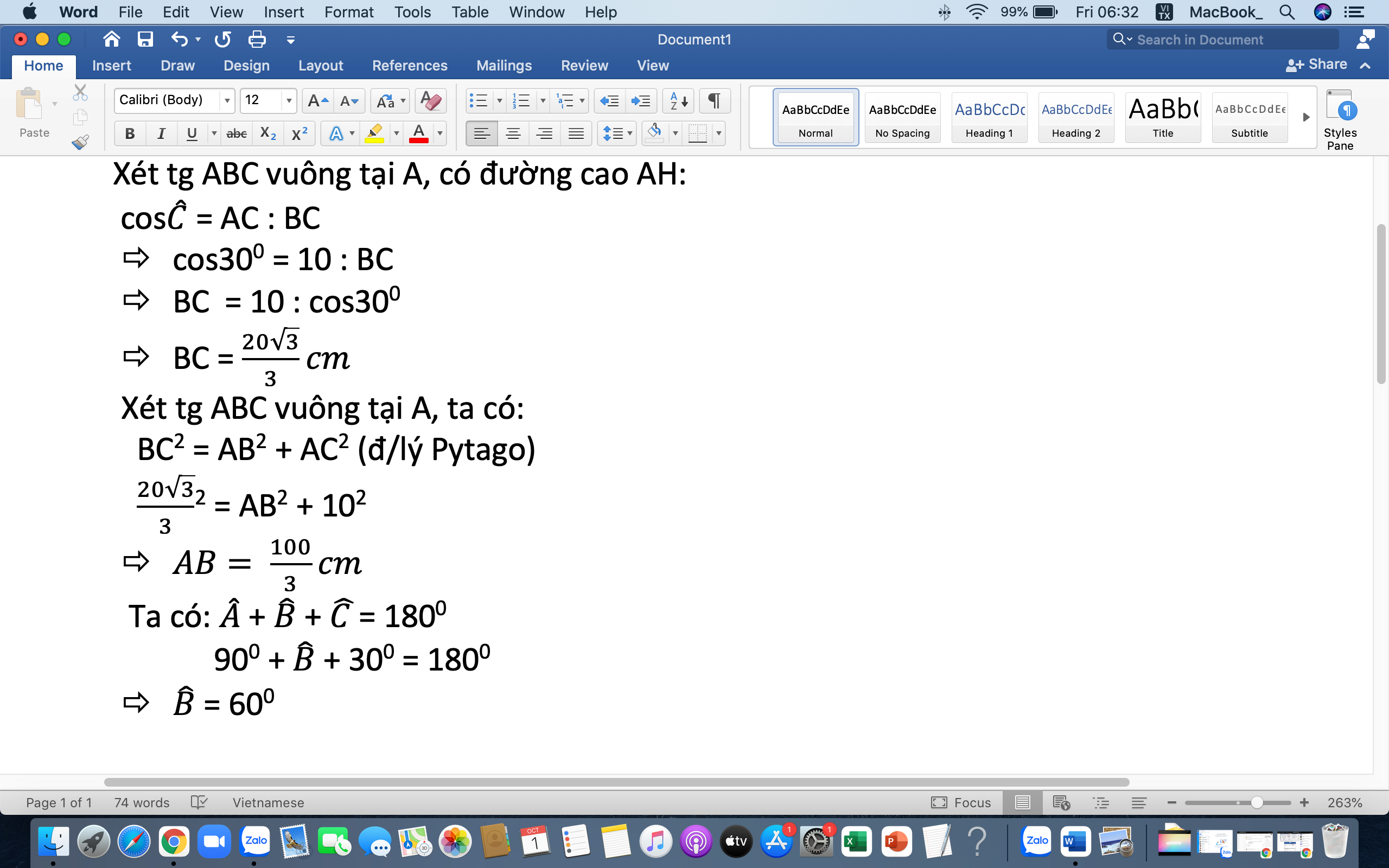
trong \(\Delta ABC\) vuông tại A
AB=AC.tanC=10.tan30=5,77
CB=\(\sqrt{AC^2+AB^2}=\sqrt{10^2+5,77^2}=11,55\)
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{5,77.10}{11,55}=5\)
\(\widehat{B}=90-\widehat{C}=90-30=60\)

\(\sqrt{a+2016}\)- \(\sqrt{a+2013}\) = (\(\sqrt{a+2016}\)- \(\sqrt{a+2013}\)) . (\(\sqrt{a+2016}+\)\(\sqrt{a+2013}\)) / \(\sqrt{a+2016}+\)\(\sqrt{a+2013}\)[ nhân cả tử và mẫu với (\(\sqrt{a+2016}+\)\(\sqrt{a+2013}\)), (mẫu cũ =1) ]
= (a+2016)-(a+2013)/\(\sqrt{a+2016}+\)\(\sqrt{a+2013}\)
k mk nha
\(\frac{\left(a+2016\right)-\left(a+2013\right)}{\sqrt{a+2016}+\sqrt{a+2013}}\)\(=\frac{\left(\sqrt{a+2016}\right)^2-\left(\sqrt{a+2013}\right)^2}{\sqrt{a+2016}+\sqrt{a+2013}}=\frac{\left(\sqrt{a+2016}+\sqrt{a+2013}\right)\left(\sqrt{a+2016}-\sqrt{a-2013}\right)}{\sqrt{a+2016}+\sqrt{a+2013}}\)
\(=\sqrt{a+2016}-\sqrt{a+2013}\)
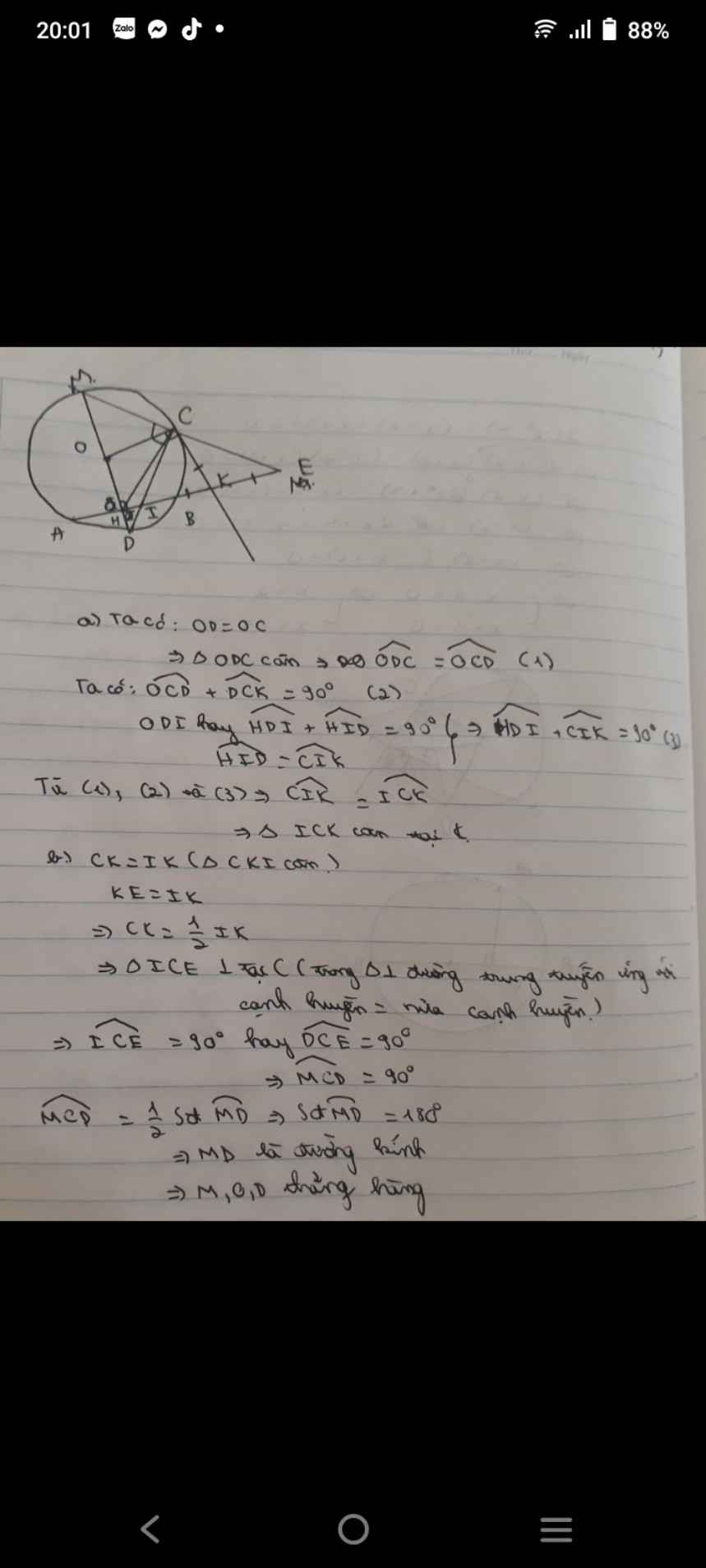
 Giải chi tiết giúp mình đc không , và giải thích tại sao các góc bằng nhau và tại sao góc đó bằng 90 độ
Giải chi tiết giúp mình đc không , và giải thích tại sao các góc bằng nhau và tại sao góc đó bằng 90 độ 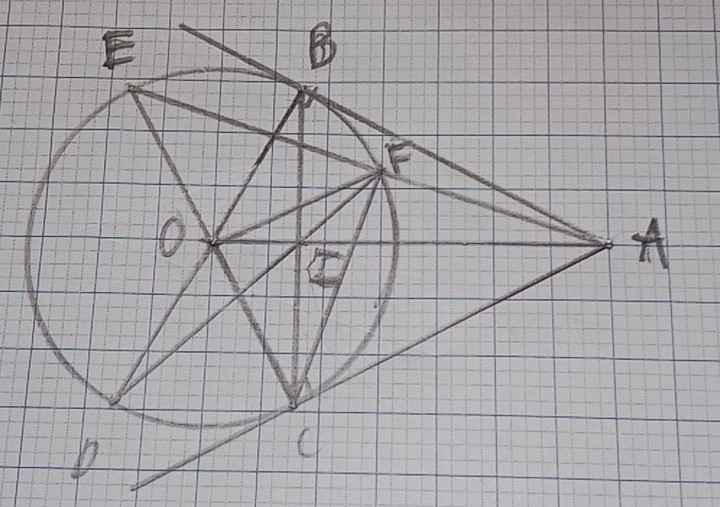



\(\widehat{MCD}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat{MCD}=90^0\Rightarrow\widehat{DCE}=180^0-90^0=90^0\)
\(\Rightarrow\widehat{ICE}=90^0\) (ICE và DCE là cùng 1 góc)