TT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 7 2020
c/
\(\Leftrightarrow\sqrt{2}sin\left(3x-\frac{\pi}{4}\right)=\frac{\sqrt{3}}{\sqrt{2}}\)
\(\Leftrightarrow sin\left(3x-\frac{\pi}{4}\right)=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\left[{}\begin{matrix}3x-\frac{\pi}{4}=\frac{\pi}{3}+k2\pi\\3x-\frac{\pi}{4}=\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{7\pi}{36}+\frac{k2\pi}{3}\\x=\frac{11\pi}{36}+\frac{k2\pi}{3}\end{matrix}\right.\)
d/
\(\Leftrightarrow2sinx.cosx+1-2sin^2x=1\)
\(\Leftrightarrow2sinx\left(cosx-sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sinx=cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{\pi}{4}+k\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 7 2020
a/
\(\Leftrightarrow\frac{\sqrt{3}}{2}sin5x-\frac{1}{2}cos5x=-1\)
\(\Leftrightarrow sin\left(5x-\frac{\pi}{6}\right)=-1\)
\(\Leftrightarrow5x-\frac{\pi}{6}=-\frac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=-\frac{\pi}{15}+\frac{k2\pi}{5}\)
b/
\(\Leftrightarrow\frac{1}{2}sinx-\frac{\sqrt{3}}{2}cosx=\frac{1}{2}\)
\(\Leftrightarrow sin\left(x-\frac{\pi}{3}\right)=\frac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\frac{\pi}{3}=\frac{\pi}{6}+k2\pi\\x-\frac{\pi}{3}=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k2\pi\\x=\frac{7\pi}{6}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 7 2020
c/
\(\Leftrightarrow\sqrt{3}sin3x-cos3x=sin2x-\sqrt{3}cos2x\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}sin3x-\frac{1}{2}cos3x=\frac{1}{2}sin2x-\frac{\sqrt{3}}{2}cos2x\)
\(\Leftrightarrow sin\left(3x-\frac{\pi}{6}\right)=sin\left(2x-\frac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\frac{\pi}{6}=2x-\frac{\pi}{3}+k2\pi\\3x-\frac{\pi}{6}=\pi-2x+\frac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{6}+k2\pi\\x=\frac{3\pi}{10}+\frac{k2\pi}{5}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 7 2020
e/
\(\Leftrightarrow\frac{1}{2}sin8x-\frac{\sqrt{3}}{2}cos8x=\frac{\sqrt{3}}{2}sin6x+\frac{1}{2}cos6x\)
\(\Leftrightarrow sin\left(8x-\frac{\pi}{3}\right)=sin\left(6x+\frac{\pi}{6}\right)\)
\(\Rightarrow\left[{}\begin{matrix}8x-\frac{\pi}{3}=6x+\frac{\pi}{6}+k2\pi\\8x-\frac{\pi}{3}=\pi-6x-\frac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=\frac{\pi}{28}+\frac{k\pi}{7}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 10 2020
\(\frac{\sqrt{3}}{2}sin3x-\frac{1}{2}cos3x+sin\frac{9x}{4}=2\)
\(\Leftrightarrow sin\left(3x-\frac{\pi}{6}\right)+sin\left(\frac{9x}{4}\right)=2\)
Do \(\left\{{}\begin{matrix}sin\left(3x-\frac{\pi}{6}\right)\le1\\sin\left(\frac{9x}{4}\right)\le1\end{matrix}\right.\)
Nên đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}sin\left(3x-\frac{\pi}{6}\right)=1\\sin\left(\frac{9x}{4}\right)=1\end{matrix}\right.\)
\(\Leftrightarrow x=\frac{2\pi}{9}+\frac{k8\pi}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 7 2020
c/
\(\Leftrightarrow\frac{1}{2}cosx-\frac{\sqrt{3}}{2}sinx=cos3x\)
\(\Leftrightarrow cos\left(x+\frac{\pi}{3}\right)=cos3x\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{\pi}{3}=3x+k2\pi\\x+\frac{\pi}{3}=-3x+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k\pi\\x=\frac{\pi}{12}+\frac{k\pi}{2}\end{matrix}\right.\)
d/
\(\Leftrightarrow\frac{1}{2}sin3x-\frac{\sqrt{3}}{2}cos3x=sin2x\)
\(\Leftrightarrow sin\left(3x-\frac{\pi}{3}\right)=sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\frac{\pi}{3}=2x+k2\pi\\3x-\frac{\pi}{3}=\pi-2x+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}+k2\pi\\x=\frac{4\pi}{15}+\frac{k2\pi}{5}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 7 2020
a/
\(\Leftrightarrow\frac{1}{2}sinx+\frac{\sqrt{3}}{2}cosx=sin\left(x+\frac{\pi}{6}\right)\)
\(\Leftrightarrow sin\left(x+\frac{\pi}{3}\right)=sin\left(x+\frac{\pi}{6}\right)\)
\(\Rightarrow x+\frac{\pi}{3}=\pi-x-\frac{\pi}{6}+k2\pi\)
\(\Rightarrow x=\frac{\pi}{4}+k\pi\)
b/
\(\Leftrightarrow\frac{\sqrt{3}}{2}sinx+\frac{1}{2}cosx=sin\frac{\pi}{12}\)
\(\Leftrightarrow sin\left(x+\frac{\pi}{6}\right)=sin\frac{\pi}{12}\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{\pi}{6}=\frac{\pi}{12}+k2\pi\\x+\frac{\pi}{6}=\frac{11\pi}{12}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{12}+k2\pi\\x=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)
3 tháng 4 2017
a) cosx - √3sinx = √2 ⇔ cosx - tan
sinx = √2
⇔ coscosx - sinsinx = √2cos ⇔ cos(x + ) = 
⇔ 
3 tháng 4 2017
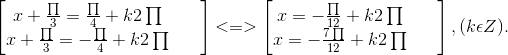
b) 3sin3x - 4cos3x = 5 ⇔ 
sin3x - 
cos3x = 1.
Đặt α = arccos thì phương trình trở thành
cosαsin3x - sinαcos3x = 1 ⇔ sin(3x - α) = 1 ⇔ 3x - α = 
+ k2π
⇔ x = 
, k ∈ Z (trong đó α = arccos).
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 7 2020
\(sin3x-sinx+sin2x=0\)
\(\Leftrightarrow2cos2x.sinx+2sinx.cosx=0\)
\(\Leftrightarrow sinx\left(cos2x+cosx\right)=0\)
\(\Leftrightarrow2sinx.cos\frac{3x}{2}.cos\frac{x}{2}=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=0\\cos\frac{x}{2}=0\\cos\frac{3x}{2}=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\\frac{x}{2}=\frac{\pi}{2}+k\pi\\\frac{3x}{2}=\frac{\pi}{2}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\pi+k2\pi\\x=\frac{\pi}{3}+\frac{k2\pi}{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{\pi}{3}+\frac{k2\pi}{3}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 7 2020
\(cosx+cos3x+cos2x+cos4x=0\)
\(\Leftrightarrow2cos2x.cosx+2cos3x.cosx=0\)
\(\Leftrightarrow cosx\left(cos2x+cos3x\right)=0\)
\(\Leftrightarrow2cosx.cos\frac{5x}{2}.cos\frac{x}{2}=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=0\\cos\frac{x}{2}=0\\cos\frac{5x}{2}=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\\frac{x}{2}=\frac{\pi}{2}+k\pi\\\frac{5x}{2}=\frac{\pi}{2}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=\pi+k2\pi\\x=\frac{\pi}{5}+\frac{k2\pi}{5}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2020
1.
\(\Leftrightarrow cos3x=-\frac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=40^0+k120^0\\x=-40^0+k120^0\end{matrix}\right.\)
\(\Rightarrow x=\left\{40^0;160^0;80^0\right\}\)
2.
Bạn coi lại đề, số \(-\sqrt{3}\) bên vế trái ko hề hợp lý, toán cho cấp 1 như vầy còn được chứ cấp 3 chắc ko ai cho đề kiểu vậy đâu
3.
\(\Leftrightarrow\sqrt{3}sin3x-cos3x=-sin5x-\sqrt{3}cos5x\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}sin3x-\frac{1}{2}cos3x=-\left(\frac{1}{2}sin5x+\frac{\sqrt{3}}{2}cos5x\right)\)
\(\Leftrightarrow sin\left(3x-\frac{\pi}{6}\right)=sin\left(-5x-\frac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\frac{\pi}{6}=-5x-\frac{\pi}{3}+k2\pi\\3x-\frac{\pi}{6}=\frac{4\pi}{3}+5x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{48}+\frac{k\pi}{4}\\x=-\frac{7\pi}{12}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\sqrt{3}sin3x-cos3x=2sin2x\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}sin3x-\frac{1}{2}cos3x=sin2x\)
\(\Leftrightarrow sin\left(3x-\frac{\pi}{6}\right)=sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\frac{\pi}{6}=2x+k2\pi\\3x-\frac{\pi}{6}=\pi-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{7\pi}{30}+\frac{k2\pi}{5}\end{matrix}\right.\)