K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 5 2018
a)Thay m=-2 vào biểu thức ta có:
\(\left(2.-2\right)\left(x+3\right)=-\left(-2\right)x+5\)
\(\Leftrightarrow-4\left(x+3\right)=4x+5\)
\(\Leftrightarrow-4x-12=4x+5\)
\(\Leftrightarrow-4x-4x=12+5\)
\(\Leftrightarrow-8x=17\)
\(\Leftrightarrow x=\dfrac{-17}{8}\)
Nếu m=-2 thì \(x=\dfrac{-17}{8}\)
còn m=\(\dfrac{1}{2}\) thì bạn làm tương tự
mấy câu kia lát mình làm sau giờ mình bận rồi
AT
30 tháng 5 2018
a/ +) Với m = -2 ta có:
\(\left(2\cdot\left(-2\right)-1\right)\left(x+3\right)=-\left(-2x\right)+5\)
\(\Leftrightarrow-5\left(x+3\right)=2x+5\Leftrightarrow-5x-2x=5+15\)
\(\Leftrightarrow-7x=20\Leftrightarrow x=-\dfrac{20}{7}\)
Vậy khi m = -2 thì x = -20/7
+) Với m = 1/2 ta có:
\(\left(2\cdot\dfrac{1}{2}-1\right)\left(x+3\right)=-\dfrac{1}{2}x+5\)
\(\Leftrightarrow\dfrac{1}{2}x=5\Leftrightarrow x=10\)
Vậy khi m = 1/2 thì x = 10
b/ pt có nghiệm = -2
=> \(2m-1=2m+5\Leftrightarrow0\cdot m=6\left(voli\right)\)
Vậy không có gt của m nào t/m để pt có nghiệm x = -2
c/ (2m-1)(x+3) = -mx + 5
\(\Leftrightarrow2mx+6m-x+mx-3=5\)
\(\Leftrightarrow3mx-x=5-6m+3\)
\(\Leftrightarrow x\left(3m-1\right)=-6m+8\Leftrightarrow x=\dfrac{-6m+8}{3m-1}\)
AL
25 tháng 2 2019
a) Thay a = -1 vào phương trình
\(\dfrac{x-1}{x+3}+\dfrac{x-3}{x+1}=2\)
\(\Rightarrow\dfrac{x^2-1+x^2-9}{\left(x+3\right)\left(x+1\right)}=2\)
\(\Rightarrow2x^2-10=2\left(x+3\right)\left(x+1\right)=2x^2+8x+6\)
\(\Rightarrow2x^2+8x+6-2x^{10}+10=0\)
\(\Rightarrow8x+16=0\Rightarrow x=-2\)
b, c Làm tương tự như câu a
d)
Phương trình nhận x = 1 làm nghiệm
=> \(\dfrac{1+a}{1+3}+\dfrac{1-3}{1-a}=2\)
\(\Rightarrow\dfrac{a+1}{4}+\dfrac{2}{a-1}=2\)
\(\Rightarrow\dfrac{a^2-1+8}{4\left(a-1\right)}=2\)
\(\Rightarrow a^2+7=2\left(4a-1\right)=8a-2\)
\(\Rightarrow a^2-8x+9=0\)
\(\Rightarrow\left[{}\begin{matrix}a=4+\sqrt{7}\\a=4-\sqrt{7}\end{matrix}\right.\)
BG
2
PT
6 tháng 2 2019
ta có : x^5+2x^4+3x^3+3x^2+2x+1=0
\(\Leftrightarrow\)x^5+x^4+x^4+x^3+2x^3+2x^2+x^2+x+x+1=0
\(\Leftrightarrow\)(x^5+x^4)+(x^4+x^3)+(2x^3+2x^2)+(x^2+x)+(x+1)=0
\(\Leftrightarrow\)x^4(x+1)+x^3(x+1)+2x^2(x+1)+x(x+1)+(x+1)=0
\(\Leftrightarrow\)(x+1)(x^4+x^3+2x^2+x+1)=0
\(\Leftrightarrow\)(x+1)(x^4+x^3+x^2+x^2+x+1)=0
\(\Leftrightarrow\)(x+1)[x^2(x^2+x+1)+(x^2+x+1)]=0
\(\Leftrightarrow\)(x+1)(x^2+x+1)(x^2+1)=0
VÌ x^2+x+1=(x+\(\dfrac{1}{2}\))^2+\(\dfrac{3}{4}\)\(\ne0\) và x^2+1\(\ne0\)
\(\Rightarrow\)x+1=0
\(\Rightarrow\)x=-1
CÒN CÂU B TỰ LÀM (02042006)
14 tháng 2 2023
b: x^4+3x^3-2x^2+x-3=0
=>x^4-x^3+4x^3-4x^2+2x^2-2x+3x-3=0
=>(x-1)(x^3+4x^2+2x+3)=0
=>x-1=0
=>x=1
22 tháng 4 2021
a) ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
Ta có: \(\dfrac{x+1}{x-2}-\dfrac{5}{x+2}=\dfrac{12}{x^2-4}+1\)
\(\Leftrightarrow\dfrac{\left(x+1\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{5\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{12}{\left(x-2\right)\left(x+2\right)}+\dfrac{x^2-4}{\left(x-2\right)\left(x+2\right)}\)
Suy ra: \(x^2+3x+2-5x+10=12+x^2-4\)
\(\Leftrightarrow x^2-2x+12-8-x^2=0\)
\(\Leftrightarrow-2x+4=0\)
\(\Leftrightarrow-2x=-4\)
hay x=2(loại)
Vậy: \(S=\varnothing\)
22 tháng 4 2021
b) Ta có: \(\left|2x+6\right|-x=3\)
\(\Leftrightarrow\left|2x+6\right|=x+3\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+6=x+3\left(x\ge-3\right)\\-2x-6=x+3\left(x< -3\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-x=3-6\\-2x-x=3+6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\left(nhận\right)\\x=-3\left(loại\right)\end{matrix}\right.\)
Vậy: S={-3}
PD
1
AM
2 tháng 3 2018
a. Ta có: x+2-m(3x+1)=5
\(\Leftrightarrow\)x(1-3m)-3-m=0 (1)
Để pt trên là pt bậc nhất thì (1-3m) khác 0
\(\Rightarrow m\ne\dfrac{1}{3}\)
b. Thay m=1 vào (1) ta có:
x(1-3.1)-3-1=0
\(\Leftrightarrow\) x=-2
S
2
10 tháng 5 2022
a, ĐKXĐ : x ≠ 4
b,
\(\Leftrightarrow3x+2=2\left(x-4\right)\)
\(\Leftrightarrow3x+2=2x-8\)
\(\Leftrightarrow x=-10\) (N)
Vậy : ...
ND
8 tháng 2 2018
a. Với a = -3 ta được:
\(\dfrac{x+3}{x-3}-\dfrac{x-3}{x+3}+\dfrac{27-3}{x^2-9}=0\)
\(\Leftrightarrow\dfrac{\left(x+3\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}-\dfrac{\left(x-3\right)\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{24}{\left(x-3\right)\left(x+3\right)}=0\)
\(\Leftrightarrow x^2+6x+9-x^2+6x-9+24=0\)
\(\Leftrightarrow12x+24=0\)
\(\Leftrightarrow x=-2\)
8 tháng 2 2018
Giải phương trình :
\(\dfrac{x-a}{x+a}-\dfrac{x+a}{x-a}+\dfrac{3a^2+a}{x^2-a^2}=0\)
a) Với a = -3
\(\dfrac{x-3}{x+3}-\dfrac{x+3}{x-3}+\dfrac{27+3}{x^2-3^2}=0\)
ĐKXĐ : \(\left\{{}\begin{matrix}x+3\ne0\\x-3\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne-3\\x\ne3\end{matrix}\right.\)
Ta có : \(\dfrac{x-3}{x+3}-\dfrac{x+3}{x-3}+\dfrac{27+3}{x^2-3^2}\)
\(\Leftrightarrow\) \(\dfrac{\left(x-3\right)\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{\left(x+3\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{27+3}{\left(x+3\right)\left(x-3\right)}=0\)
Khử mẫu ta có : \(\left(x-3\right)^2-\left(x+3\right)^2+27+3=0\)
⇔ \(x^2+6x+9-x^2+6x-9+30=0\)
\(\Leftrightarrow12x+30=0\)
\(\Leftrightarrow12x=-30\)
\(\Leftrightarrow x=-\dfrac{5}{2}\)
Tập nghiệm của pt là: \(S=\left\{-\dfrac{5}{2}\right\}\)
b) Với a = 1
\(\dfrac{x-1}{x+1}-\dfrac{x+1}{x-1}+\dfrac{3+3}{x^2-1}=0\)
ĐKXĐ : \(\left\{{}\begin{matrix}x+1\ne0\\x-1\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne-1\\x\ne1\end{matrix}\right.\)
Ta có : \(\dfrac{x-1}{x+1}-\dfrac{x+1}{x-1}+\dfrac{3+3}{x^2-1}=0\)
\(\Leftrightarrow\) \(\dfrac{\left(x-1\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}-\dfrac{\left(x+1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{3+3}{\left(x+1\right)\left(x-1\right)}=0\)
Khử mẫu ta có : \(\left(x-1\right)^2-\left(x+1\right)^2+6=0\)
\(\Leftrightarrow x^2+x-1-x^2+x+1+6=0\)
\(\Leftrightarrow2x+6=0\)
\(\Leftrightarrow2x=-6\)
\(\Leftrightarrow x=-3\)
Tập nghiệm của pt là : \(S=\left\{-3\right\}\)
1 tháng 5 2018
Bài 1 :
a) \(a\ne x\)
b) Tại a= 2 PT
\(\Leftrightarrow\left(5.2-8\right)x=2014\)
\(\Leftrightarrow2x=2014\)
\(\Leftrightarrow x=1007\)
Vậy tập nghiệm của phương trình đã cho khi a=2 là \(S=\left(1007\right)\)
Bài 2
Ta có :\(f\left(x\right)=2x^2-12x+14\)
\(=2\left(x^2-6x+9\right)-4\)
\(=2\left(x-3\right)^2-4\ge-4\)
Dấu \("="\Leftrightarrow x-3=0\Leftrightarrow x=3\)
Vậy GTNN của \(f\left(x\right)\)là \(-4\)khi \(x=3\)
Nhớ K cho tớ nhé
PD
1
25 tháng 2 2018
Điều kiện a để phương trình là phương trình bậc nhất là : a # 0
Với a = -3 , pt có dạng :
-9x - 1 - 3 = 0
<=> -9x = 4
<=> x = \(\dfrac{-4}{9}\)
Vậy,....
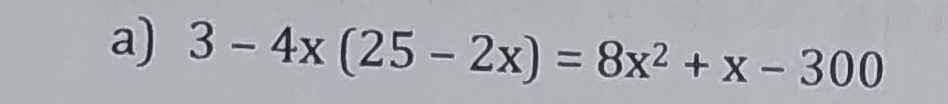
3 - 4x(25 - 2x) = 8x² + x - 300
3 - 100x + 8x² = 8x² + x - 300
-100x + 8x² - 8x² - x = -300 - 3
-101x = -303
x = -303 : (-101)
x = 3
Vậy S = {3}