K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 3 2019
Bài 1 :
a )Thế \(m=1\) vào phương trình ta được :
\(2x^2-3x-2=0\)
\(\Leftrightarrow2x^2+x-4x-2=0\)
\(\Leftrightarrow x\left(2x+1\right)-2\left(2x+1\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\frac{1}{2}\\x=2\end{matrix}\right.\)
Vậy \(S=\left\{-\frac{1}{2};2\right\}\)
b ) Theo hệ thức vi-et ta có :
\(\left\{{}\begin{matrix}x_1+x_2=\frac{6m-3}{2}\\x_1x_2=\frac{-3m+1}{2}\end{matrix}\right.\)
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(\frac{6m-3}{2}\right)^2-\frac{2\left(-3m+1\right)}{2}\)
\(=\frac{36m^2-36m+9}{4}+3m-1\)
\(=\frac{36m^2-36m+9+12m-4}{4}\)
\(=\frac{36m^2-24m+5}{4}\)
\(=\frac{36m^2-24m+4+1}{4}\)
\(=\frac{\left(6m-2\right)^2+1}{4}\ge\frac{1}{4}\)
Vậy GTNN của A là \(\frac{1}{4}\) . Dấu bằng xảy ra khi \(x=\frac{1}{3}\)
NH
1
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 12 2021
\(\Leftrightarrow x^2-2x+2-\left(x+2\right)\sqrt{x^2-2x+2}+3x-3=0\)
Đặt \(\sqrt{x^2-2x+2}=a>0\)
\(\Rightarrow a^2-\left(x+2\right)a+3x-3=0\)
\(\Delta=\left(x+2\right)^2-4\left(3x-3\right)=\left(x-4\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}a=\dfrac{x+2+x-4}{2}=x-1\\a=\dfrac{x+2-\left(x-4\right)}{2}=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x^2-2x+2}=x-1\left(vn\right)\\\sqrt{x^2-2x+2}=3\end{matrix}\right.\)
\(\Rightarrow x^2-2x-7=0\)
13 tháng 12 2021
thầy ơi máy tính em bị lỗi hay sao mà ra nghiệm 8950000 vậy ạ?
17 tháng 9 2021
a: Ta có: \(\sqrt{x^2}=x\)
\(\Leftrightarrow\left|x\right|=x\)
hay \(x\ge0\)
b: Ta có: \(\sqrt{x^2-4x+4}=x-2\)
\(\Leftrightarrow\left|x-2\right|=x-2\)
\(\Leftrightarrow x\ge2\)
17 tháng 9 2021
\(\sqrt{x^2}=x\Leftrightarrow\left|x\right|=x\Leftrightarrow x\ge0\)
\(\sqrt{x^2-4x+4}=x-2\left(x\in R\right)\\ \Leftrightarrow\left|x-2\right|=x-2\\ \Leftrightarrow x-2\ge0\Leftrightarrow x\ge2\)
NV
2
NT
17 tháng 3 2016
https://coccoc.com/search/math#query=gi%E1%BA%A3i+pt+(2x-2)%2F(x%5E2-36)+-+(x-2)%2F(x%5E2-6x)+%3D+(x-1)%2F(x%5E2%2B6x)
19 tháng 5 2021
`(x^2-x)(x^2-x+1)=6`
Đặt `a=x^2-x(x>=-1/4)`
`pt<=>a(a+1)=6`
`<=>a^2+a-6=0`
`Delta=1+24=25`
`=>a_1=-2(l),a_2=1(tm)`
`<=>x^2-x=1`
`<=>x^2-x-1=0`
`Delta=1+4=5`
`=>x_{12}=(+-sqrt5+1)/2`
19 tháng 5 2021
\(\left(x^2-x\right)\left(x^2-x+1\right)=6\)
\(\Leftrightarrow\left(x^2-x\right)^2+\left(x^2-x\right)-6=0\)
\(\Leftrightarrow\left[\left(x^2-x\right)-2\right]\left[\left(x^2-x\right)+3\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-x=2\\x^2-x=-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-x-2=0\\x^2-x+3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-2\right)\left(x+1\right)=0\\\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}=0\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow\)\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
N
1
DN
2 tháng 7 2021
`x^2 + 2(m-1)x + m^2 = 0`
Thay `m=0` vào pt và giải ta được :
`x^2 - 6x + 16 = 0`
Vì `x^2 - 6x + 16 > 0` với mọi `x`
`=>` vô nghiệm
Vậy `S = RR`
Thay `m=-4` vào pt và giải ta được :
`x^2 + 10x + 16 = 0`
`\Delta = 10^2 - 4*1*16 = 36 > 0`
`=> \sqrt{\Delta} = 6`
`=>` Phương trình có 2 nghiệm phân biệt :
`x_1 = (-10+6)/(2*1) = -2`
`x_2 = (-10-6)/(2*1) = -8`
Vậy `S = {-2,-8}`
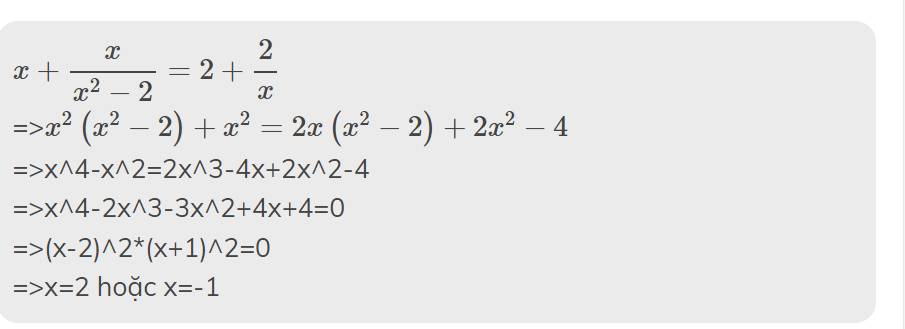
\(x+\dfrac{x}{x^2-2}=2+\dfrac{2}{x}\)
=>\(x^2\left(x^2-2\right)+x^2=2x\left(x^2-2\right)+2x^2-4\)
=>x^4-x^2=2x^3-4x+2x^2-4
=>x^4-2x^3-3x^2+4x+4=0
=>(x-2)^2*(x+1)^2=0
=>x=2 hoặc x=-1