
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 7. a) sin 3x - cos 5x = 0 ⇔ cos 5x = sin 3x ⇔ cos 5x = cos (![]() - 3x) ⇔
- 3x) ⇔
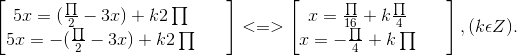
b) tan 3x . tan x = 1 ⇔ ![]() . Điều kiện : cos 3x . cos x # 0.
. Điều kiện : cos 3x . cos x # 0.
Với điều kiện này phương trình tương đương với
cos 3x . cos x = sin 3x . sinx ⇔ cos 3x . cos x - sin 3x . sinx = 0 ⇔ cos 4x = 0.
Do đó
tan 3x . tan x = 1 ⇔ ![]()
![]()
⇔ cos 2x = ![]() ⇔ cos 4x = 0
⇔ cos 4x = 0
⇔ ![]()


\(tan3x=tanx\)
Điều kiện: \(x \ne \dfrac{\pi }{6} + \dfrac{{k\pi }}{3},k \in Z\)
\( \Leftrightarrow \tan 3x - {\mathop{\rm tanx}\nolimits} = 0\\ \Leftrightarrow \dfrac{{\sin 2x}}{{\cos 3x.cosx}} = 0\\ \Leftrightarrow \sin 2x = 0\\ \Leftrightarrow 2x = k\pi \\ \Leftrightarrow x = \dfrac{{k\pi }}{2},k \in Z \)
Chọn A



Lời giải:
$\tan 3x-\tan x=2$
$\Leftrightarrow \frac{3\tan x-\tan ^3x}{1-3\tan ^2x}-\tan x=2$
Đặt $\tan x=a$ thì:
$\frac{3a-a^3}{1-3a^2}-a=2$
$\Leftrightarrow a^3+3a^2+a-1=0$
$\Leftrihgtarrow a^2(a+1)+2a(a+1)-(a+1)=0$
$\Leftrightarrow (a+1)(a^2+2a-1)=0$
$\Leftrightarrow a=-1$ hoặc $a=-1\pm \sqrt{2}$
Đến đây thì đơn giản rồi.
ĐKXĐ: \(\left\{{}\begin{matrix}x\ne\dfrac{\pi}{2}+k\pi\\x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{3}\end{matrix}\right.\)
\(\dfrac{sin3x}{cos3x}-\dfrac{sinx}{cosx}=2\)
\(\Rightarrow sin3x.cosx-cos3x.sinx=2cos3x.cosx\)
\(\Leftrightarrow sin2x=cos4x-cos2x\)
\(\Leftrightarrow cos^22x-sin^22x-sin2x-cos2x=0\)
\(\Leftrightarrow\left(sin2x+cos2x\right)\left(cos2x-sin2x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)=0\\cos\left(2x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)

a.
\(cos\left(3x-\frac{\pi}{6}\right)=sin\left(2x+\frac{\pi}{3}\right)\)
\(\Leftrightarrow cos\left(3x-\frac{\pi}{6}\right)=cos\left(\frac{\pi}{6}-2x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\frac{\pi}{6}=\frac{\pi}{6}-2x+k2\pi\\3x-\frac{\pi}{6}=2x-\frac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
b.
ĐKXĐ: \(\left\{{}\begin{matrix}cosx\ne0\\cos3x\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\cos2x\ne\frac{1}{2}\end{matrix}\right.\)
\(tan3x-tanx=0\)
\(\Leftrightarrow\frac{sin3x}{cos3x}-\frac{sinx}{cosx}=0\)
\(\Leftrightarrow sin3x.cosx-cos3x.sinx=0\)
\(\Leftrightarrow sin2x=0\)
\(\Leftrightarrow2sinx.cosx=0\)
\(\Leftrightarrow sinx=0\Leftrightarrow x=k\pi\)
c.
\(\Leftrightarrow\frac{1}{2}+\frac{1}{2}cos\left(2x-\frac{2\pi}{5}\right)=\frac{1}{2}-\frac{1}{2}cos\left(4x+\frac{8\pi}{5}\right)\)
\(\Leftrightarrow cos\left(2x-\frac{2\pi}{5}\right)=-cos\left(4x+\frac{3\pi}{5}+\pi\right)\)
\(\Leftrightarrow cos\left(2x-\frac{2\pi}{5}\right)=cos\left(4x+\frac{3\pi}{5}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+\frac{3\pi}{5}=2x-\frac{2\pi}{5}+k2\pi\\4x+\frac{3\pi}{5}=\frac{2\pi}{5}-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
d.
\(\Leftrightarrow cos^2\left(2x-1\right)=0\)
\(\Leftrightarrow cos\left(2x-1\right)=0\)
\(\Leftrightarrow x=\frac{\pi}{4}+\frac{1}{2}+\frac{k\pi}{2}\)

a.
\(\Leftrightarrow2sin\frac{17\pi}{30}cos\left(3x-\frac{7\pi}{30}\right)=\sqrt{3}\)
\(\Leftrightarrow cos\left(3x-\frac{7\pi}{30}\right)=\frac{\sqrt{3}}{2sin\left(\frac{17\pi}{30}\right)}\)
Đặt \(\frac{\sqrt{3}}{2sin\left(\frac{17\pi}{30}\right)}=cosa\) với \(a\in\left(0;\pi\right)\)
\(\Rightarrow cos\left(3x-\frac{7\pi}{30}\right)=cosa\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\frac{7\pi}{30}=a+k2\pi\\3x-\frac{7\pi}{30}=-a+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{7\pi}{90}+\frac{a}{3}+\frac{k2\pi}{3}\\x=\frac{7\pi}{30}-\frac{a}{3}+\frac{k2\pi}{3}\end{matrix}\right.\)
Chắc bạn ghi sai đề, con số \(\frac{4\pi}{3}\) sẽ hợp lý hơn con số \(\frac{4\pi}{5}\) rất nhiều

ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{3}\)
\(tan3x=tanx\)
\(\Leftrightarrow3x=x+k\pi\)
\(\Leftrightarrow x=\dfrac{k\pi}{2}\)
Đối chiếu điều kiện ta được \(x=k\pi\) là nghiệm của phương trình.