K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
0
DN
29 tháng 10 2017
)2+3(x+1)2{7x2−22x+28=(2x−1)2+3(x−3)27x2+8x+13=(2x−1)2+3(x+2)231x2+14x+4=7(2x−1)2+3(x+1)2
Do đó:
VT≥3–√|3−x|+3–√|x+2|+3–√|x+1|≥3–√(3−x)+3–√(x+2)+3–√(x+1)=33–√(x+2)VT≥3|3−x|+3|x+2|+3|x+1|≥3(3−x)+3(x+2)+3(x+1)=33(x+2)
TK
20 tháng 8 2020
to gefhfhdgtggg
GGGGGG
GGGGG
G
G
G
G
G
G
G
G
G
G
GG
GG
G
G
G
G
G
GG
G
GGG
G
G
G
G
G
G
G
G
G
G
GG
G
G
G
G
G
G
G
GG
G
GG
G
G
G
G
G
G
G
G
G
G
G
G
G
GG
GG
G
G
G
GG
GGGGG
G
G
G
G
G
G
G
GGGGG
G
G
GG
GG
GG
G
G
G
GGG
G
G
GG
G
GGG
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
G
GG
GG
G
G
GG
F
E
RE
R
ER
\\\\\\]
YYYYYYYYY
CMMCMMCMMCMMCMMMCMCMMCMCMCMC
N
G
U
V
L
AHIHI
TD
0
28 tháng 8 2021
a: Ta có: \(x^2+3x+4=0\)
\(\text{Δ}=3^2-4\cdot1\cdot4=9-16=-7< 0\)
Do đó: Phương trình vô nghiệm
14 tháng 2 2018
\(5x^2-22x+23=0\)
\(\Leftrightarrow25x^2-110x+115=0\)
\(\Leftrightarrow\left(5x\right)^2-2.5x.11+121=6\)
\(\Leftrightarrow\left(5x-11\right)^2=6\)
\(\Leftrightarrow5x-11=\pm\sqrt{6}\)
\(\Leftrightarrow x=\frac{11\pm\sqrt{6}}{5}\)
Vậy...
KN
0
KN
31 tháng 5 2019
\(x^4-6x^2-8x-3=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+1\right)^3=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\x+1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=-1\end{cases}}\)
Vậy tập nghiệm \(S=\left\{-1;3\right\}\)
31 tháng 5 2019
\(x^4-3x^3+3x^3-9x^2+3x^2-9x+x-3=0\)
\(x^3\left(x-3\right)+3x^2\left(x-3\right)+3x\left(x-3\right)+\left(x-3\right)=0\)
\(\left(x-3\right)\left(x^3+3x^2+3x+1\right)=0\)
\(\left(x-3\right)\left(x+1\right)^3=0\)
=> \(x-3=0\)hoặc \(x+1=0\)
=> x=3 hoặc x=-1
NA
1
AH
Akai Haruma
Giáo viên
12 tháng 8 2021
Lời giải:
ĐKXĐ: $x\geq -3,5$
PT \(\Leftrightarrow (\sqrt{2x+7}-1)+(\sqrt[3]{x+4}-1)+(x^2+8x+15)=0\)
\(\Leftrightarrow \frac{2(x+3)}{\sqrt{2x+7}+1}+\frac{x+3}{\sqrt[3]{(x+4)^2}+\sqrt[3]{x+4}+1}+(x+3)(x+5)=0\)
\(\Leftrightarrow (x+3)\left[\frac{2}{\sqrt{2x+7}+1}+\frac{1}{\sqrt[3]{(x+4)^2}+\sqrt[3]{x+4}+1}+(x+5)\right]=0\)
Với $x\geq -3,5$ dễ thấy biểu thức trong ngoặc vuông $>0$
Do đó: $x+3=0$
$\Leftrightarrow x=-3$ (thỏa mãn)
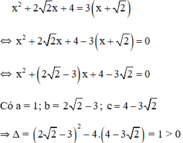
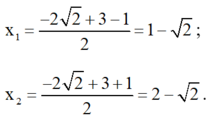
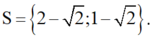
\(\Leftrightarrow x^4-18x^2+81-4x^2-8x-4=0\)
\(\Leftrightarrow\left(x^2-9\right)^2-\left(2x+2\right)^2=0\)
\(\Leftrightarrow\left(x^2-9-2x-2\right)\left(x^2-9+2x+2\right)=0\)
\(\Leftrightarrow\left(x^2-2x-10\right)\left(x^2+2x-7\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2-2x-10=0\\x^2+2x-7=0\end{cases}\Leftrightarrow\orbr{\begin{cases}\left(x-1\right)^2=\pm\left(\sqrt{11}\right)^2\\\left(x+1\right)^2=\pm\left(\sqrt{8}\right)^2\end{cases}}}\)
ĐẾN ĐÂY BẠN TỰ LÀM NHÉ
X= \(1+\sqrt{11}\),X=\(-1+\sqrt{11}\)
X=\(-1-2\sqrt{2}\),X=\(-1+2\sqrt{2}\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x-1\right)^2=\pm\left(\sqrt{11}\right)\\\left(x+1\right)^2=\pm\left(\sqrt{8}\right)\end{cases}\Leftrightarrow\orbr{\begin{cases}\orbr{\begin{cases}x=1+\sqrt{11}\\x=1-\sqrt{11}\end{cases}}\\\orbr{\begin{cases}x=-1+2\sqrt{2}\\x=-1-2\sqrt{2}\end{cases}}\end{cases}}}\)