
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



√(2x²+8x+6) + √(x²-1) = 2(x+1) TXĐ: x € (-∞;-3] U [1;+∞) U {-1}
Từ pt => x≥ -1. Kết hợp với TXĐ đc: x ≥1 hoặc x = -1
Bình phương 2 vế:
2√[2(x²-1)(x²+4x+3)] = x²-1
Từ đây suy ra x² ≥ 1, lại bình phương 2 vế tiếp:
8(x²-1)(x²+4x+3) = x^4 - 2x²+1
<=> 7x^4 + 32x³ + 18x² -32x -25 = 0
<=> 7x^4 - 7x² + 32x³ - 32x +25x² - 25 = 0
<=> 7x²(x²-1) + 32x(x²-1) +25(x²-1) = 0
<=> (x²-1)(7x²+32x+25) = 0
<=> (x²-1)(x+1)(7x+25) = 0
<=> x = ±1 (x = -25/7 loại)
hình như bạn hiểu sai đề rồi. viết lại cho rõ nhé:(8x-6)căn (x-1)=(2+căn (x-2))(x+4 căn(x-2)+3)

Lời giải:
Điều kiện \(x\geq 0\)
\(\text{PT}\Leftrightarrow 2(x^2+2x+4)=3\sqrt{4x(x^2+4)}\)
Áp dụng bất đẳng thức AM-GM:
\(2(x^2+2x+4)=3\sqrt{4x(x^2+4)}\leq 3\left (\frac{4x+x^2+4}{2}\right)\)
\(\Rightarrow 4(x^2+2x+4)\leq 3(x^2+4x+4)\Leftrightarrow (x-2)^2\leq 0\)
Ta biết rằng \((x-2)^2\geq 0\forall x\in\mathbb{R}\) nên dấu bằng xảy ra khi \(x=2\)
Vậy \(x=2\) là nghiệm của phương trình.

điều kiện : \(\begin{cases}x\ne1\\x\ne2\end{cases}\)
phương trình: \(\Leftrightarrow\left(x+m\right)\left(x-2\right)=\left(x+3\right)\left(x-1\right)\)
\(\Leftrightarrow x^2+\left(m-2\right)x-2m=x^2+2x-3\)
\(\Leftrightarrow\left(m-4\right)x=2m-3\)
+ m = 4 phương trình vô nghiệm
+ m\(\ne\) 4 phương trình \(\Leftrightarrow x=\frac{2m-3}{m-4}\)
do điều kiện : \(\begin{cases}x\ne1\\x\ne2\end{cases}\)nên \(\begin{cases}\frac{2m-3}{m+1}\ne1\\\frac{2m-3}{m-4}\ne2\end{cases}\) \(\Leftrightarrow\) \(\begin{cases}2m-3\ne m-4\\2m-3\ne2m-8\end{cases}\)
\(\Leftrightarrow m\ne-1\)
vậy: + \(m\in\left\{4;-1\right\}\): phương trình vô nghiệm
+ \(m\in R\text{ /}\left\{4;-1\right\}\) :phương trình có nghiệm duy nhất \(x=\frac{2m-3}{m-4}\)

Đặt a=x+4 ta được:
(a-1)4+(a+1)4=16
<=>2a4+6a2+2=16
<=>2a4+12a2-14=0
Đặt t=a2(t\(\ge\) 0) ta được:
2t2+12t-14=0
\(\Delta=256\Rightarrow\sqrt{\Delta}=16;\Delta>0,\text{pt có 2 nghiệm phân biệt: }t_1=1\left(thỏa\right);t_2=-7\left(loại\right)\)
t=1=>a2=1 =>a=\(\pm1\)
Với a=1 =>x=-3
Với a=-1 =>x=-5
Đặt a=x+4 ta được:
(a-1)4+(a+1)4=16
<=>2a4+6a2+2=16
<=>2a4+12a2-14=0
Đặt t=a2(t≥≥ 0) ta được:
2t2+12t-14=0
Δ=256⇒Δ−−√=16;Δ>0,pt có 2 nghiệm phân biệt: t1=1(thỏa);t2=−7(loại)Δ=256⇒Δ=16;Δ>0,pt có 2 nghiệm phân biệt: t1=1(thỏa);t2=−7(loại)
t=1=>a2=1 =>a=±1±1
Với a=1 =>x=-3
Với a=-1 =>x=-5
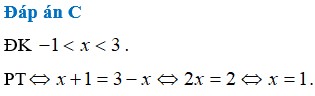
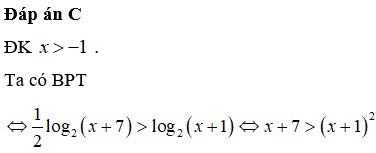
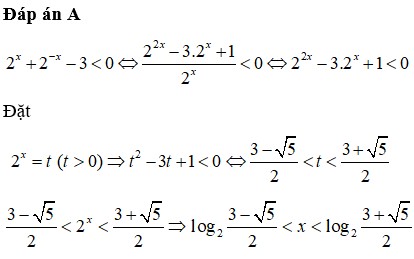
ta có:
\(\left|x+3\right|\ge0;\left|x-3\right|\ge0\)
\(\Rightarrow\left|x+3\right|+\left|x-3\right|\ge0\Rightarrow7-x\ge0\Rightarrow-x\ge-7\Rightarrow x\le-7\)
\(\Rightarrow x+3\le-4\Rightarrow\left|x+3\right|=-x-3\)
và \(x-3\le-10\Rightarrow\left|x-3\right|=3-x\)
Thay \(\left|x+3\right|=-x-3\) và \(\left|x-3\right|=3-x\) vào phương trình, ta được:
\(\text{- x - 3 + 3 - x = 7 - x}\)
\(\Rightarrow-2x=7-x\Rightarrow-x=7\Rightarrow x=-7\)
Vậy x = - 7
ta có:
|x+3|≥0;|x−3|≥0|x+3|≥0;|x−3|≥0
⇒|x+3|+|x−3|≥0⇒7−x≥0⇒−x≥−7⇒x≤−7⇒|x+3|+|x−3|≥0⇒7−x≥0⇒−x≥−7⇒x≤−7
⇒x+3≤−4⇒|x+3|=−x−3⇒x+3≤−4⇒|x+3|=−x−3
và x−3≤−10⇒|x−3|=3−xx−3≤−10⇒|x−3|=3−x
Thay |x+3|=−x−3|x+3|=−x−3 và |x−3|=3−x|x−3|=3−x vào phương trình, ta được:
- x - 3 + 3 - x = 7 - x- x - 3 + 3 - x = 7 - x
⇒−2x=7−x⇒−x=7⇒x=−7⇒−2x=7−x⇒−x=7⇒x=−7
Vậy x = - 7