K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 4 2020
Ta có:\(\frac{x-2}{2017}+1+\frac{x-3}{2018}+1=\frac{x-4}{2019}+1+\frac{x-5}{2020}+1\)
\(\Rightarrow\frac{x+2015}{2017}+\frac{x+2015}{2018}-\frac{x+2015}{2019}-\frac{x+2015}{2020}=0\)
\(\Rightarrow\left(x+2015\right)\left(\frac{1}{2017}+\frac{1}{2018}-\frac{1}{2019}-\frac{1}{2020}\right)=0\)
Mà \(\frac{1}{2017}+\frac{1}{2018}-\frac{1}{2019}-\frac{1}{2020}>0\)
\(\Rightarrow x+2015=0\Rightarrow x=-2015\)
\(S=\left\{-2015\right\}\)
24 tháng 5 2022
Nhận thấy vế trái luôn dương nên \(x-2020\ge0\Leftrightarrow x\ge2020\)
Với \(x\ge2020\Rightarrow\left\{{}\begin{matrix}x-2017\ge0\\2x-2018\ge0\\3x-2019\ge0\end{matrix}\right.\)
PT trở thành: \(x-2017+2x-2018+3x-2019=x-2020\)
Hay kết hợp với điều kiện \(x=\dfrac{4034}{5}\) suy ra PT đã cho vô nghiệm
P
0
AH
Akai Haruma
Giáo viên
14 tháng 10 2021
Lời giải:
a.
PT $\Leftrightarrow (x+3)^2=2016^{2020}-17^{91}+9$
Ta thấy: $2016^{2020}-17^{91}+9\equiv 0-(-1)^{91}+0\equiv -1\equiv 2\pmod 3$
Mà 1 scp thì chia $3$ chỉ dư $0$ hoặc $1$ nên pt vô nghiệm.
b.
$x^2=2016(y-1)^2-2017^{2019}\equiv 0-1^{2019}\equiv 3\pmod 4$
Mà 1 scp chia $4$ chỉ dư $0$ hoặc $1$ nên vô lý.
Vậy pt vô nghiệm.
c.
$(x-1)^2=2017^{2017}+1\equiv 1^{2017}+1\equiv 2\pmod 4$
Mà 1 scp khi chia cho $4$ chỉ dư $0$ hoặc $1$ nên vô lý
Vậy pt vô nghiệm
d.
$(x+2)^2=2018^{10}+4\equiv (-1)^{10}+1\equiv 2\pmod 3$
Mà 1 scp khi chia $3$ dư $0$ hoặc $1$ nên vô lý
Vậy pt vô nghiệm.
HP
0
3 tháng 3 2020
Đề: \(\frac{x-2}{2020}+\frac{x-3}{2019}=\frac{x-4}{2018}+\frac{x-5}{2017}\)
⇔ \(\left(\frac{x-2}{2020}-1\right)+\left(\frac{x-3}{2019}-1\right)=\left(\frac{x-4}{2018}-1\right)+\left(\frac{x-5}{2017}-1\right)\)
⇔ \(\frac{x-2022}{2020}+\frac{x-2022}{2019}=\frac{x-2022}{2018}+\frac{x-2022}{2017}\)
⇔\(\frac{x-2022}{2020}+\frac{x-2022}{2019}-\frac{x-2022}{2018}-\frac{x-2022}{2017}=0\)
⇔ \(\left(x-2022\right)\)\(\left(\frac{1}{2020}+\frac{1}{2019}-\frac{1}{2018}-\frac{1}{2017}\right)\) = 0
Nên x - 2022 = 0 ⇔ x = 2022
Mà \(\left(\frac{1}{2020}+\frac{1}{2019}-\frac{1}{2018}-\frac{1}{2017}\right)\)≠0
Vậy nghiệm của pt là x = 2022
HN
19 tháng 3 2021
\(\dfrac{x+1}{2020}+\dfrac{x+2}{2019}+\dfrac{x+3}{2018}+\dfrac{x+4}{2017}+4=0\)
⇔ \(\dfrac{x+1}{2020}+1+\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1+\dfrac{x+4}{2017}+1=0\)
\(\Leftrightarrow\) \(\dfrac{x+2021}{2020}+\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}+\dfrac{x+2021}{2017}=0\)
⇔ \(\left(x+2021\right)\left(\dfrac{1}{2020}+\dfrac{1}{2019}+\dfrac{1}{2018}+\dfrac{1}{2017}\right)=0\)
\(Do\) \(\left(\dfrac{1}{2020}+\dfrac{1}{2019}+\dfrac{1}{2018}+\dfrac{1}{2017}\right)\ne0\)
⇒ \(x+2021=0\)
⇔ \(x=-2021\)
\(Vậy\) \(x=-2021\)
HH
1
TT
15 tháng 5 2021
\(\dfrac{x+1}{2021}+\dfrac{x+2}{2020}=\dfrac{x+3}{2019}+\dfrac{x+4}{2018}\)
=>\(\dfrac{x+1}{2021}+1+\dfrac{x+2}{2020}+1=\dfrac{x+3}{2019}+1+\dfrac{x+4}{2018}+1\)
=>\(\dfrac{x+2022}{2021}+\dfrac{x+2022}{2020}=\dfrac{x+2022}{2019}+\dfrac{x+2022}{2018}\)
=> (x+2022)(\(\dfrac{1}{2021}+\dfrac{1}{2020}-\dfrac{1}{2019}-\dfrac{1}{2018}\))=0
=>x+2022=0
=> x=-2022
OM
5 tháng 4 2020
a, Làm
\(\frac{x+1}{2020}+\frac{x+2}{2019}+\frac{x+3}{2018}=\frac{x+4}{2017}+\frac{x+5}{2016}+\frac{x+6}{2015}\)
<=>\(\frac{x+2021}{2020}+\frac{x+2021}{2019}+\frac{x+2021}{2018}=\frac{x+2021}{2017}+\frac{x+2021}{2016}+\frac{x+2021}{2015}\)
<=>\(\left(x+2021\right)\left(\frac{1}{2020}+\frac{1}{2019}+\frac{1}{2018}-\frac{1}{2017}-\frac{1}{2016}-\frac{1}{2015}\right)=0\)
<=> x+2021=0
<=> x=-2021
Kl:......................
b, Làmmmmm
\(\frac{2-x}{2004}-1=\frac{1-x}{2005}-\frac{x}{2006}\)
<=> \(\frac{2006-x}{2004}=\frac{2006-x}{2005}+\frac{2006-x}{2006}\)
<=> \(\left(2006-x\right)\left(\frac{1}{2004}-\frac{1}{2005}-\frac{1}{2006}\right)=0< =>2006-x=0\)
<=> x=2006
Kl:..............
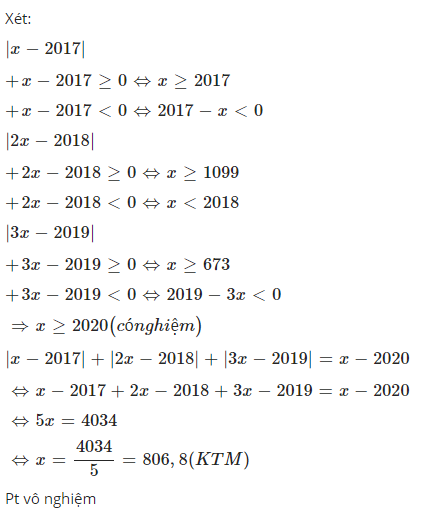
\(\frac{x-2}{2017}+\frac{x-3}{2018}=\frac{x-4}{2019}+\frac{x-5}{2020}\)
<=> \(\frac{x-2}{2017}+1+\frac{x-3}{2018}+1=\frac{x-4}{2019}+1+\frac{x-5}{2020}+1\)
<=> \(\frac{x+2015}{2017}+\frac{x+2015}{2018}-\frac{x+2015}{2019}-\frac{x+2015}{2020}=0\)
<=> \(\left(x+2015\right)\left(\frac{1}{2017}+\frac{1}{2018}-\frac{1}{2019}-\frac{1}{2020}\right)=0\)
<=> x + 2015 = 0 ( vì \(\frac{1}{2017}+\frac{1}{2018}-\frac{1}{2019}-\frac{1}{2020}\ne0\))
<=> x = - 2015
Vậy x = -2015.
Giải phương trình :
\(\frac{x-2}{2017}+\frac{x-3}{2018}=\frac{x-4}{2019}+\frac{x-5}{2020}\)
\(\Rightarrow\frac{x-2}{2017}+1+\frac{x-3}{2018}+1=\frac{x-4}{2019}+1+\frac{x-5}{2020}+1\)
\(\Rightarrow\frac{x+2015}{2017}+\frac{x+2015}{2018}-\frac{x+2015}{2019}-\frac{x+2015}{2020}=0\)
\(\Rightarrow\left(x+2015\right)\left(\frac{1}{2017}+\frac{1}{2018}-\frac{1}{2019}-\frac{1}{2020}\right)=0\)
Mà \(\left(\frac{1}{2017}+\frac{1}{2018}-\frac{1}{2019}-\frac{1}{2020}\right)>0\)
\(\Rightarrow x+2015=0\)
\(\Rightarrow x=-2015\)