Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\frac{x+\frac{x+1}{5}}{3}=1-\frac{2x-\frac{1-2x}{34}}{5}\)
\(\Leftrightarrow\frac{\frac{5x+x+1}{5}}{3}=1-\frac{\frac{68x-1+2x}{34}}{5}\)
\(\Leftrightarrow\frac{6x+1}{15}=1-\frac{70-1}{170}\)
\(\Leftrightarrow\frac{6x+1}{15}+\frac{70x-1}{170}-1=0\)
\(\Leftrightarrow\frac{34\left(6x+1\right)+3\left(70x-1\right)-510}{510}=0\)
\(\Leftrightarrow204x+34+210x-3-510=0\)
\(\Leftrightarrow414x-479=0\)
\(\Leftrightarrow x=\frac{479}{414}\)
Vậy tập nghiệm của phương trình là \(S=\left\{\frac{479}{414}\right\}\)

a.\(\dfrac{1}{x}\)-\(\dfrac{1}{x+1}\)=\(\dfrac{x+1}{x\left(x+1\right)}\)-\(\dfrac{x}{x\left(x+1\right)}\)=\(\dfrac{x+1-x}{x\left(x+1\right)}\)=\(\dfrac{1}{x\left(x+1\right)}\)
b. Ta có:
\(\dfrac{1}{x\left(x+1\right)}\)= \(\dfrac{\left(x+1\right)-x}{x\left(x+1\right)}\)=\(\dfrac{x+1}{x\left(x+1\right)}\)-\(\dfrac{x}{x\left(x+1\right)}\)=\(\dfrac{1}{x}\)-\(\dfrac{1}{x+1}\)
Ta lại có:
\(\dfrac{1}{\left(x+1\right)\left(x+2\right)}\)=\(\dfrac{1}{x+1}\)-\(\dfrac{1}{x+2}\);
\(\dfrac{1}{\left(x+2\right)\left(x+3\right)}\)=\(\dfrac{1}{x+2}\)-\(\dfrac{1}{x+3}\);
\(\dfrac{1}{\left(x+3\right)\left(x+4\right)}\)=\(\dfrac{1}{x+3}\)-\(\dfrac{1}{x+4}\);
\(\dfrac{1}{\left(x+4\right)\left(x+5\right)}\)=\(\dfrac{1}{x+4}\)-\(\dfrac{1}{x+5}\);
Do đó:
\(\dfrac{1}{x\left(x+1\right)}\)+\(\dfrac{1}{\left(x+1\right)\left(x+2\right)}\)+\(\dfrac{1}{\left(x+2\right)\left(x+3\right)}\)+\(\dfrac{1}{\left(x+3\right)\left(x+4\right)}\)+\(\dfrac{1}{\left(x+4\right)\left(x+5\right)}\)+\(\dfrac{1}{x+5}\) = \(\dfrac{1}{x}\)-\(\dfrac{1}{x+1}\)+\(\dfrac{1}{x+1}\)-\(\dfrac{1}{x+2}\)+\(\dfrac{1}{x+2}\)-...... -\(\dfrac{1}{x+5}\)+\(\dfrac{1}{x+5}\)=\(\dfrac{1}{x}\)
Vậy tổng trên bằng \(\dfrac{1}{x}\)

Bài 6
\(\left(a-b\right)^2=a^2-2ab+b^2\)
\(=\left(a^2+2ab+b^2\right)-4ab\)
\(=\left(a+b\right)^2-4ab\)
Bài 5 :
\(a,16x^2-\left(4x-5\right)^2=15\)
\(16x^2-16x^2+40x-25-15=0\)
\(40x-40=0\)
\(40x=40\)
\(x=1\)
\(b,\left(2x+3\right)^2-4\left(x-1\right)\left(x+1\right)=49\)
\(4x^2+12x+9-4x^2+4=49\)
\(12x=36\)
\(x=3\)
\(c,\left(2x+1\right)\left(2x-1\right)+\left(1-2x\right)^2=18\)
\(4x^2-1+1-4x+4x^2=18\)
\(8x^2-4x-18=0\)
\(2\left(4x^2-2x-9\right)=0\)
\(x=\frac{1-\sqrt{37}}{4}\)
\(d,2\left(x+1\right)^2-\left(x-3\right)\left(x+3\right)-\left(x-4\right)^2=0\)
\(2x^2+4x+2-x^2+9-x^2+8x-16=0\)
\(12x=4\)
\(x=\frac{1}{3}\)

a)
\(\dfrac{x-3}{5}+\dfrac{1-2x}{3}=6\\ < =>3x-9+5-10x=90\)
\(< =>3x-10x=90+9-5\\ < =>-7x=94\\ < =>x=-\dfrac{94}{7}\)
b)
\(\left(2x-3\right)\left(x^2+1\right)=0\\ < =>\left[{}\begin{matrix}2x-3=0\\x^2+1=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{3}{2}\\x^2=-1\left(voli\right)\end{matrix}\right.\\ < =>x=\dfrac{3}{2}\)
c)
\(\dfrac{2}{x+1}-\dfrac{1}{x-2}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\left(x\ne-1;x\ne2\right)\)
suy ra: \(2\left(x-2\right)-x-1=3x-11\)
\(< =>2x-4-x-1-3x+11=0\)
\(< =>2x-x-3x=4+1-11\\ < =>-2x=-6\\ < =>x=3\left(tm\right)\)
a) \(\dfrac{x-3}{5}+\dfrac{1-2x}{3}=6\)
\(\Leftrightarrow3\left(x-3\right)+5\left(1-2x\right)=90\)
\(\Leftrightarrow-4-7x=90\)
\(\Leftrightarrow x=-\dfrac{94}{7}\)
b) \(\left(2x-3\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow2x-3=0\) (Vì \(x^2+1>0\))
\(\Leftrightarrow x=\dfrac{3}{2}\)
c) \(\dfrac{2}{x+1}-\dfrac{1}{x-2}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\left(Đk:x\ne-1;x\ne2\right)\)
\(\Leftrightarrow2\left(x-2\right)-\left(x+1\right)=3x-11\)
\(\Leftrightarrow x-5=3x-11\)
\(\Leftrightarrow x=3\)

\(\dfrac{\left(2x+1\right)^2}{5}-\dfrac{\left(x-1\right)^2}{3}=\dfrac{7x^2-14x-5}{15}\)
=> \(\dfrac{3\left(4x^2+4x+1\right)-5\left(x^2-2x+1\right)}{15}\) \(=\dfrac{7x^2-14x-5}{15}\)
=> \(\dfrac{7x^2+22x-2}{15}=\dfrac{7x^2-14x-5}{15}\)
=> \(\dfrac{7x^2+22x-2-7x^2+14x+5}{15}=0\)
=>\(\dfrac{36x+3}{15}=0\)
=> 36x=-3
=>\(x=\dfrac{-1}{12}\)
Vay \(S=\left\{\dfrac{-1}{12}\right\}\)
Phương trình tương đương: \(3\left(4x^2+4x+1\right)-5\left(x^2-2x+1\right)=7x^2-14x-5\\ \Leftrightarrow7x^2+22x+3=7x^2-14x\\ \Leftrightarrow22x+3=-14x\\ \Leftrightarrow22x+14x=-3\\ \Leftrightarrow36x=-3\\ \Leftrightarrow x=-\dfrac{1}{12}\)
Vậy \(S=\left\{-\dfrac{1}{2}\right\}\)

e sẽ cố gắng !!!
\(3x-15=2x\left(x-5\right)\)
\(3x-15=2x^2-10x\)
\(3x-15-2x^2+10x=0\)
\(13x-15-2x^2=0\)
\(x\left(13-2x\right)-15=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\13-2x-15=0\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\-2-2x=0\end{cases}\Rightarrow}\orbr{\begin{cases}x=0\\2x=-2\end{cases}\Rightarrow}\orbr{\begin{cases}x=0\\x=-1\end{cases}}}\)
\(f,x\left(2x-7\right)-4x+14=0\)
\(2x^2-7x-4x+14=0\)
\(2x^2-11x+14=0\)
\(x\left(2x-11\right)=-14\)
\(\Rightarrow\orbr{\begin{cases}x=-14\\2x-11=-14\end{cases}\Rightarrow\orbr{\begin{cases}x=-14\\2x=-3\end{cases}\Rightarrow}\orbr{\begin{cases}x=-14\\x=-\frac{3}{2}\end{cases}}}\)

a) \(\frac{1-x}{x+1}+3=\frac{2x+3}{x+1}\)
<=> 1 - x + 3(x + 1) = 2x + 3
<=> 1 - x + 3x + 3 = 2x + 3
<=> 1 - x + 3x + 3 - 2x = 3
<=> 4 = 3 (vô lý)
=> pt vô nghiệm
b) ĐKXĐ: \(x\ne1;x\ne2\)
\(\frac{1}{x+1}-\frac{5}{x-2}=\frac{15}{\left(x+1\right)\left(2-x\right)}\)
<=> (x - 2)(2 - x) - 5(x + 1)(2 - x) = 15(x - 2)
<=> 2x - x2 - 4 + 2x - 5x - 5x2 + 10 = 15x - 30
<=> -x + 4x2 - 14 = 15x - 30
<=> x - 4x2 + 14 = 15x - 30
<=> x - 4x2 + 14 + 15x - 30 = 0
<=> 16x - 4x2 - 16 = 0
<=> 4(4x - x2 - 4) = 0
<=> -x2 + 4x - 4 = 0
<=> x2 - 4x + 4 = 0
<=> (x - 2)2 = 0
<=> x - 2 = 0
<=> x = 2 (ktm)
=> pt vô nghiệm
c) xem bài 4 ở đây: Câu hỏi của gjfkm
d) ĐKXĐ: \(x\ne1;x\ne2;x\ne3\)
\(\frac{x+4}{x^2-3x+2}+\frac{x+1}{x^2-4x+3}=\frac{2x+5}{x^2-4x+3}\)
<=> \(\frac{x+4}{\left(x-1\right)\left(x-2\right)}+\frac{x+1}{\left(x-1\right)\left(x-3\right)}=\frac{2x+5}{\left(x-1\right)\left(x-3\right)}\)
<=> (x + 4)(x - 3) + (x + 1)(x - 2) = (2x + 5)(x - 2)
<=> x2 - 3x + 4x - 12 + x2 - 2x + x - 2 = 2x2 - 4x + 5x - 10
<=> 2x2 - 14 = 2x2 + x - 10
<=> 2x2 - 14 - 2x2 = x - 10
<=> -14 = x - 10
<=> -14 + 10 = x
<=> -4 = x
<=> x = -4

a) ( 3 - x )( x2 + 2x - 7 ) + ( x - 3 )( x2 + x - 5 )
= ( 3 - x )( x2 + 2x - 7 ) - ( 3 - x )( x2 + x - 5 )
= ( 3 - x )( x2 + 2x - 7 - x2 - x + 5 )
= ( 3 - x )( x - 2 )
b) ( x - 5 )2 + 3( 5 - x )
= ( x - 5 )2 - 3( x - 5 )
= ( x - 5 )( x - 5 - 3 ) = ( x - 5 )( x - 8 )
c) 2x( x - 1 )2 - ( 1 - x )3
= 2x( 1 - x )2 - ( 1 - x )3
= ( 1 - x )2( 2x - 1 + x ) = ( 1 - x )2( 3x - 1 )
d) x2 + 8x + 16 = ( x + 4 )2
e) x2 - 4xy + 4y2 = ( x - 2y )2
g) 4x2 - 25y2 = ( 2x )2 - ( 5y )2 = ( 2x - 5y )( 2x + 5y )
h) 25( x + 1 )2 - 4( x - 3 )2
= 52( x + 1 )2 - 22( x - 3 )2
= ( 5x + 5 )2 - ( 2x - 6 )2
= ( 5x + 5 - 2x + 6 )( 5x + 5 + 2x - 6 )
= ( 3x + 11 )( 7x - 1 )
i) x3 + 27 = ( x + 3 )( x2 - 3x + 9 )
k) 8x3 - 125 = ( 2x )3 - 53 = ( 2x - 5 )( 4x2 + 10x + 25 )
l) x3 + 6x2 + 12x + 8 = ( x + 2 )3
m) -x3 + 9x2 - 27x + 27 = -( x3 - 9x2 + 27x - 27 ) = -( x - 3 )3

1) \(x\left(2^2-3\right)-x^2\left(5x+1\right)+x^2\)
\(=x-5x^3-x^2+x\)
\(=2x-5x^3-x^2\)
2) \(\left(3x-5\right)\left(2x+11\right)-\left(2x+3\right)\left(3x+7\right)\)
\(=\left(6x^2+23x-55\right)-\left(6x^2+23x+21\right)\)
\(=-76\)
Làm lại câu 1
\(x\left(2^2-3\right)-x^2\left(5x+1\right)+x^2\)
\(=x-5x^3-x^2+x^2\)
\(=x-5x^3\)
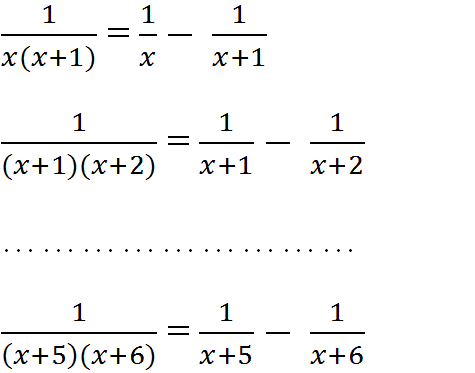
\(\dfrac{\left(2x+1\right)^2}{5}-\dfrac{\left(x-1\right)^2}{3}=\dfrac{7x^2-14x-5}{15}\)
⇔ \(\dfrac{3\left(2x+1\right)^2}{15}-\dfrac{5\left(x-1\right)^2}{15}=\dfrac{7x^2-14x-5}{15}\)
⇔ \(3\left(2x+1\right)^2-5\left(x-1\right)^2=7x^2-14x-5\)
⇔ \(3\left(4x^2+4x+1\right)-5\left(x^2-2x+1\right)=7x^2-14x-5\)
⇔ \(12x^2+12x+3-5x^2+10x-5=7x^2-14x-5\)
⇔ \(7x^2+22x-2=7x^2-14x-5\) ⇔ \(36x+3=0\) ⇔ x=\(\dfrac{-1}{12}\)
\(\Leftrightarrow3\left(4x^2+4x+1\right)-5\left(x^2-2x+1\right)=7x^2-14x-5\)
\(\Leftrightarrow12x^2+12x+3-5x^2+10x-5-7x^2+14x+5=0\)
\(\Leftrightarrow36x=-3\)
hay x=-1/12