
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\hept{\begin{cases}5x+5y=30\\y+5z=12\\3x+5z=22\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=6-y\\y+5z=12\\3x+5z=22\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y+5z=12\\3\left(6-y\right)+5z=22\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y+5z=12\\-3y+5z=4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y+5z=12\\3y-5z=-4\end{cases}}\)
\(\Rightarrow4y=8\Rightarrow y=2\)
Thay giá trị của y vào phương trình: -3y + 5z = 4
\(-3\times2+5z=4\)
\(\Rightarrow z=2\)
Thế giá trị của y vào phương trình: x = 6 - y
\(\Rightarrow x=4\)

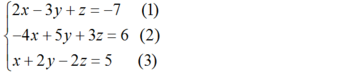
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần các ẩn.
Nhân phương trình (1) với 2 rồi cộng với phương trình (2) và nhân phương trình (3) với 4 rồi cộng với phương trình (2) ta được:
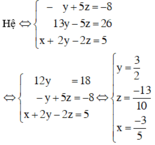
Vậy hệ phương trình có nghiệm 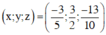

Giải các phương trình và hệ phương trình:
a) x2 - \(2\sqrt{5}\)x + 5 = 0
Ta có: x2 - \(2\sqrt{5}\)x + 5 = 0 <=> ( x = \(\sqrt{5}\) )2 = 0 <=> x - \(\sqrt{5}\) = 0 <=> x = \(\sqrt{5}\)
Vậy phương trình đã cho có tập nghiệm S = ( \(\sqrt{5}\) )
c) \(\begin{cases}2x+5y=-1\\3x-2y=8\end{cases}\) <=> \(\begin{cases}6x+15y=-3\\6x-4y=16\end{cases}\) <=> \(\begin{cases}19y=-19\\3x-2y=8\end{cases}\) <=> \(\begin{cases}y=-1\\3x-2.\left(-1\right)=8\end{cases}\) <=> \(\begin{cases}y=-1\\x=2\end{cases}\)
Vậy hệ phương trình có 1 nghiệm duy nhất (x ; y) = (2 ; -1)

mấy bài này là ở lớp 9 học kì 2 dùng cộng đại số là nhanh nhất hoặc bấm máy tính

Điều kiện \(\left\{{}\begin{matrix}\dfrac{4x-3x^2y-9xy^2}{x+3y}\ge0\\x+3y\ne0\end{matrix}\right.\)
Với \(3y\ge x\), hệ tương đương:
\(\left\{{}\begin{matrix}\left(x^4-2x^2+4\right)\left(x^2+2\right)=6x^5y\\\left(3y-x\right)^2=\dfrac{4x}{x+3y}-3xy\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^6+8=6x^5y\left(1\right)\\x^3+27y^3=4x\end{matrix}\right.\left(I\right)\)
Vì \(x=0\) thì hệ vô nghiệm nên \(x\ne0\), khi đó:
\(\left(I\right)\Leftrightarrow\left\{{}\begin{matrix}1+\dfrac{8}{x^6}=\dfrac{6y}{x}\\1+\dfrac{27y^3}{x^3}=\dfrac{4}{x^2}\end{matrix}\right.\)
Đặt \(\dfrac{3y}{x}=a,\dfrac{2}{x^2}=b\) ta được hệ:
\(\Leftrightarrow\left\{{}\begin{matrix}1+a^3=2b\\1+b^3=2a\end{matrix}\right.\)
Giải hệ này ta được \(a=b\Leftrightarrow\dfrac{3y}{x}=\dfrac{2}{x^2}\Leftrightarrow y=\dfrac{2}{3x}\)
\(\left(1\right)\Leftrightarrow x^6-4x^4+8=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{2}\\x=-\sqrt{2}\\x=\sqrt{1+\sqrt{5}}\\x=-\sqrt{1+\sqrt{5}}\end{matrix}\right.\)
TH1: \(x=\sqrt{2}\Rightarrow y=\dfrac{\sqrt{2}}{3}\)
TH2: \(x=-\sqrt{2}\Rightarrow y=-\dfrac{\sqrt{2}}{3}\)
TH3: \(x=\sqrt{1+\sqrt{5}}\Rightarrow y=\dfrac{2}{3\sqrt{1+\sqrt{5}}}\)
TH4: \(x=-\sqrt{1+\sqrt{5}}\Rightarrow y=-\dfrac{2}{3\sqrt{1+\sqrt{5}}}\)
Đối chiếu với các điều kiện ta được \(\left(x;y\right)=\left(-\sqrt{1+\sqrt{5}};-\dfrac{2}{3\sqrt{1+\sqrt{5}}}\right)\)



Đơn giản hóa 4x + 5y = 47 Giải quyết 4x + 5y = 47 Giải cho biến 'x'. Di chuyển tất cả các điều khoản có chứa x sang trái, tất cả các điều khoản khác sang phải. Thêm '-5y' vào mỗi bên của phương trình. 4x + 5y + -5y = 47 + -5y Kết hợp như các điều khoản: 5y + -5y = 0 4x + 0 = 47 + -5y 4x = 47 + -5y Chia mỗi bên cho '4'. x = 11,75 + -1,25y Đơn giản hóa x = 11,75 + -1,25y