K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 6 2021
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{2}cos\left(2x-\dfrac{\pi}{2}\right)=\dfrac{1}{2}+\dfrac{1}{2}cos2x\)
\(\Leftrightarrow-sin2x=cos2x\)
\(\Leftrightarrow sin2x+cos2x=0\)
\(\Leftrightarrow\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow2x+\dfrac{\pi}{4}=k\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{8}+\dfrac{k\pi}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 6 2021
Cách biến đổi (chứng minh) đơn giản thôi:
\(sin2x+cos2x=0\Leftrightarrow\sqrt{2}\left(\dfrac{\sqrt{2}}{2}sin2x+\dfrac{\sqrt{2}}{2}cos2x\right)=0\)
\(\Leftrightarrow\sqrt{2}\left[sin2x.cos\left(\dfrac{\pi}{4}\right)+cos2x.sin\left(\dfrac{\pi}{4}\right)\right]=0\)
\(\Leftrightarrow\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)=0\)
Hoặc bạn nhớ vài công thức hay gặp sau:
\(sina+cosa=\sqrt{2}sin\left(a+\dfrac{\pi}{4}\right)=\sqrt{2}cos\left(a-\dfrac{\pi}{4}\right)\)
\(sina-cosa=\sqrt{2}sin\left(a-\dfrac{\pi}{4}\right)=-\sqrt{2}cos\left(a+\dfrac{\pi}{4}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 7 2021
\(\Leftrightarrow4sin^2x\left(sinx+1\right)=3\left(sinx+1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+1=0\\4sin^2x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-1\\cos2x=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{2}+k2\pi\\x=\dfrac{\pi}{3}+k\pi\\x=-\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
KH
6
HP
16 tháng 8 2021
d, \(cosx-cos2x=sin3x\)
\(\Leftrightarrow2sin\dfrac{3x}{2}.sin\dfrac{x}{2}=2sin\dfrac{3x}{2}.cos\dfrac{3x}{2}\)
\(\Leftrightarrow sin\dfrac{3x}{2}.\left(sin\dfrac{x}{2}-cos\dfrac{3x}{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\dfrac{3x}{2}=0\\sin\dfrac{x}{2}=cos\dfrac{3x}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{3x}{2}=k\pi\\cos\left(\dfrac{\pi}{2}-\dfrac{x}{2}\right)=cos\dfrac{3x}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k2\pi}{3}\\x=\dfrac{\pi}{4}-k\pi\\x=-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
CM
9 tháng 3 2018
(Điều kiện xác định: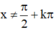 
).
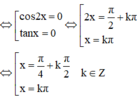
Vậy phương trình có hai họ nghiệm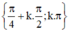 
(k ∈ Z).
CM
3 tháng 1 2019
cos 3x = cos 12º
⇔ 3x = ±12º + k.360º , k ∈ Z
⇔ x = ±4º + k.120º , k ∈ Z
Vậy phương trình có họ nghiệm x = ±4º + k.120º (k ∈ Z)
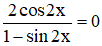
ĐKXĐ: \(sin2x\ne1\Rightarrow x\ne\dfrac{\pi}{4}+k\pi\)
\(\dfrac{2cos2x}{1-sin2x}=0\Rightarrow cos2x=0\)
\(\Rightarrow2x=\dfrac{\pi}{2}+k\pi\)
\(\Rightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Kết hợp ĐKXĐ: \(\Rightarrow x=\dfrac{3\pi}{4}+k\pi\)