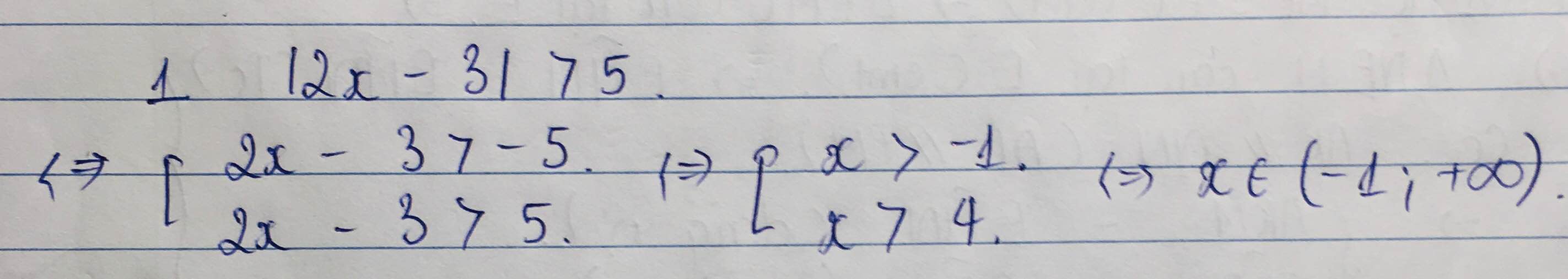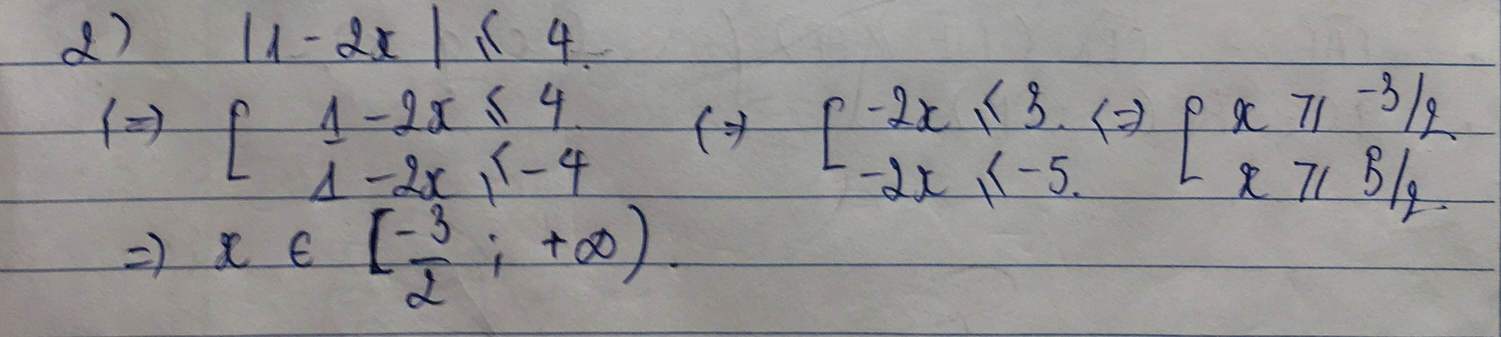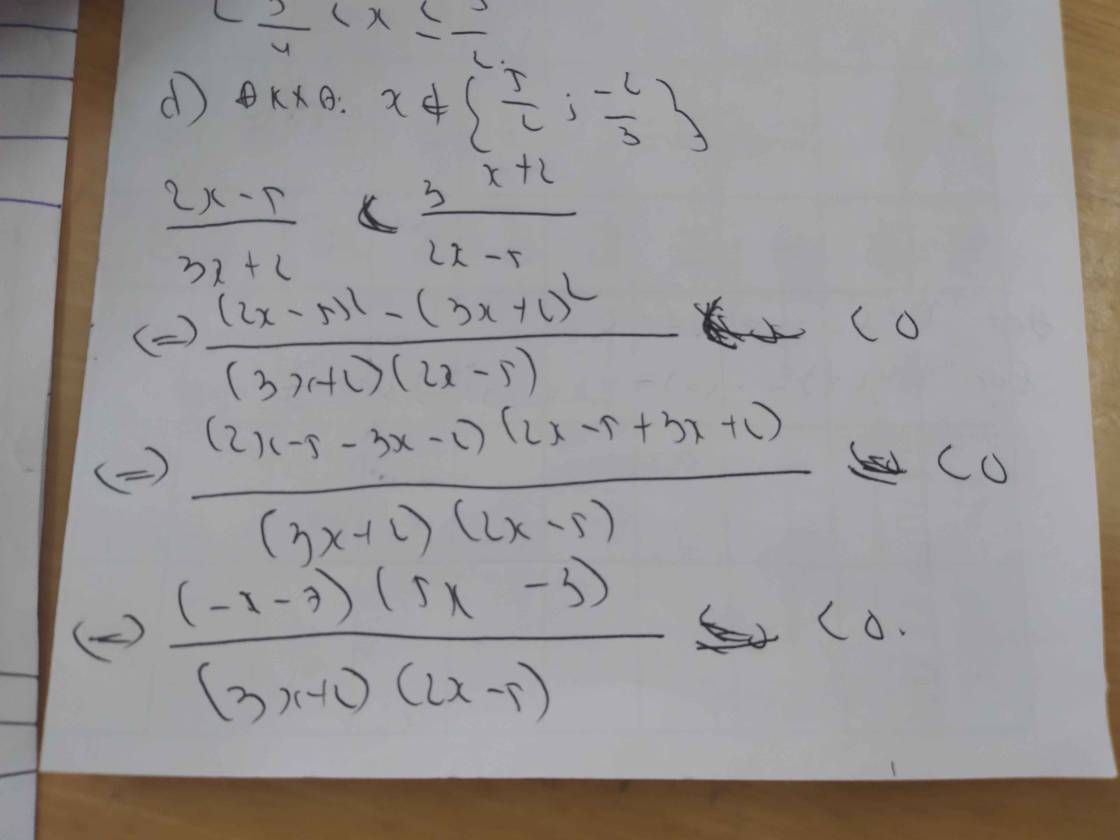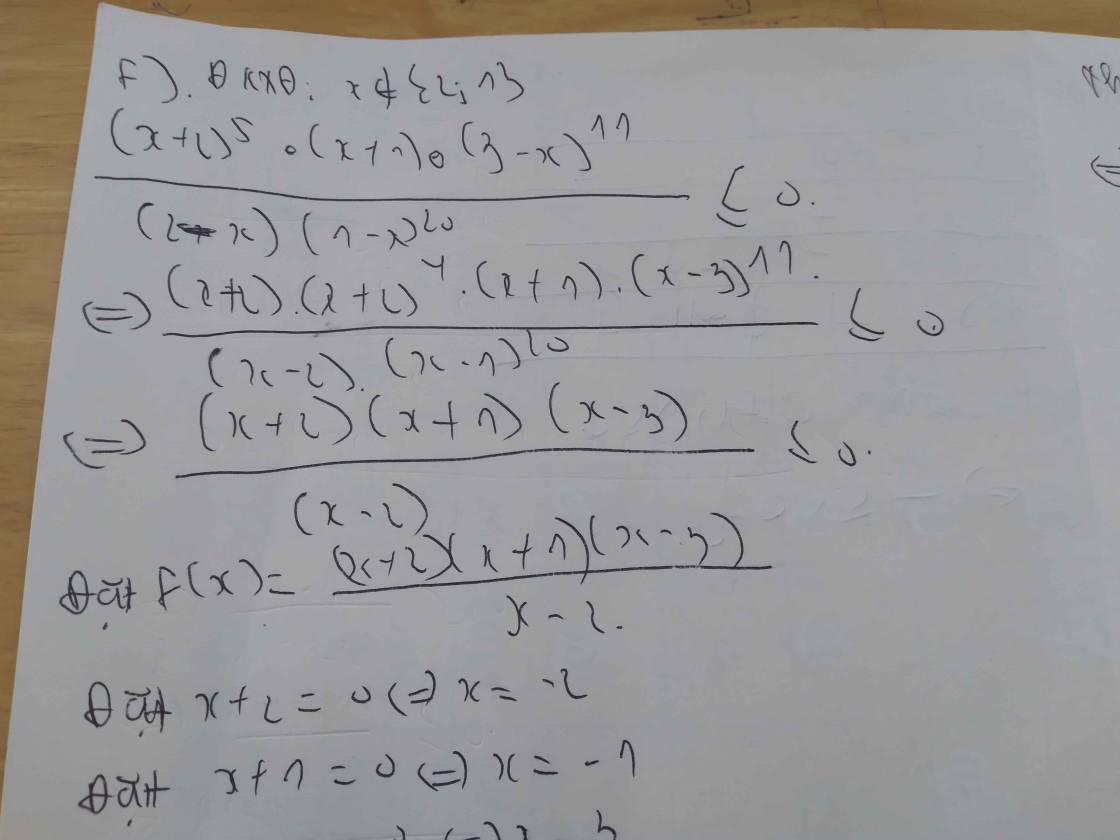Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\begin{cases}x^5-3x^4+2x^2-2x+2\ge0\\x^4-2x^3-x+2=0\\x^2-3x+2=0\\\left(x^2-1\right)\left(x-2\right)=0\end{cases}\) (*)
\(x^5-3x^4+2x^2-2x+2\ge0\) (1)
\(x^4-2x^3-x+2=0\) (2)
\(x^2-3x+2=0\) (3)
\(\left(x^2-1\right)\left(x-2\right)=0\) (4)
Từ
\(x^2-3x+2=0\) (3) \(\Leftrightarrow\) x=1 hoặc x=2
x=1 thỏa mãn tất cả các phương trình, bất phương trình còn lại nên là nghiệm của hệ
x=2 không thỏa mãn (1) nên x=2 không là nghiệm của hệ
Vậy hệ phương trình (*) có nghiệm duy nhất là x=1

1: \(\Leftrightarrow\left[{}\begin{matrix}2x-3>5\\2x-3< -5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>5\\x< -1\end{matrix}\right.\)
2: \(\Leftrightarrow-4< =2x-1< =4\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-1>=-4\\2x-1< =4\end{matrix}\right.\Leftrightarrow\dfrac{-3}{2}< =x< =\dfrac{5}{2}\)

Đặt \(y=2x^2-3x+1=2\left(x-\frac{3}{4}\right)^2-\frac{1}{8}\)
Điều kiện \(y\ge\frac{1}{8}\) (*)
Ta được hệ phương trình 2 ẩn \(x,y\)
\(\begin{cases}y=2x^2-3x+1\\x=2y^2-3y+1\end{cases}\) (a)
Trừ từng vế của hệ phương trình (a) ta được :
\(y-x=2\left(x^2-y^2\right)-3\left(x-y\right)\Leftrightarrow\left(x-y\right)\left(x+y-1\right)\)
\(\Leftrightarrow\begin{cases}y=1-\frac{\sqrt{2}}{2}\\y=1+\frac{\sqrt{2}}{2}\end{cases}\)
Cả 2 nghiệm này đều thỏa mãn điều kiện (*)
Do \(x=y\) nên ta được 2 nghiệm \(x\) tương ứng là \(x=1-\frac{\sqrt{2}}{2};x=1+\frac{\sqrt{2}}{2}\)
Thay \(x=1-y\) vào phương trình thứ 2 của hệ (a) ta được :
\(1-y=2y^2-3t+1\Leftrightarrow2y^2-2y=0\Leftrightarrow\left[\begin{array}{nghiempt}y=0\\y=1\end{array}\right.\)
Hai nghiệm này cùng thỏa mãn điều kiện (*)
Do \(x=1-y\) nên ta được 2 nghiệm \(x\) tương ứng \(x=1;x=0\)
Vậy phương trình có 4 nghiệm :
\(x=1;x=0;x=1-\frac{\sqrt{2}}{2};x=1+\frac{\sqrt{2}}{2}\)
nhận thấy vế trái có dạng là một phương trình bậc hai luôn rồi,ta chỉ cần phân tích nó thành tích của 2 cái nhân với nhau,cụ thể là
(2x^2-3x+1-1)(2(x^2-3x+1)-1)=x.
(2x^2-3x)(4x^2-6x+1)=x
x(2x-3)(4x^2-6x+1)=x
vậy x=0 hoặc (2x-3)(4x^2-6x+1)=1. bạn bấm máy tính nữa là xong.

a) \(\left(x+1\right)\left(x-1\right)\left(3x-6\right)>0\)
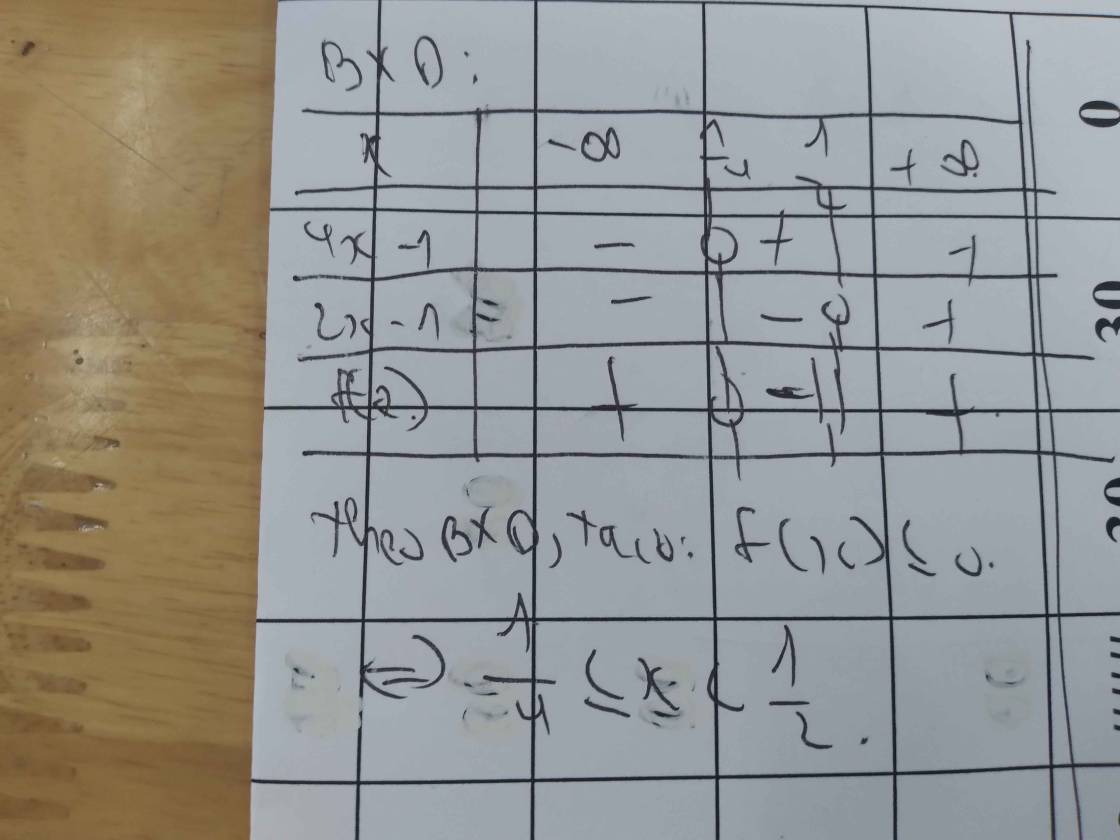
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-1< x< 1\\x>2\end{matrix}\right.\)
b) \(\dfrac{x+3}{x-2}\le0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow-3\le x< 2\)
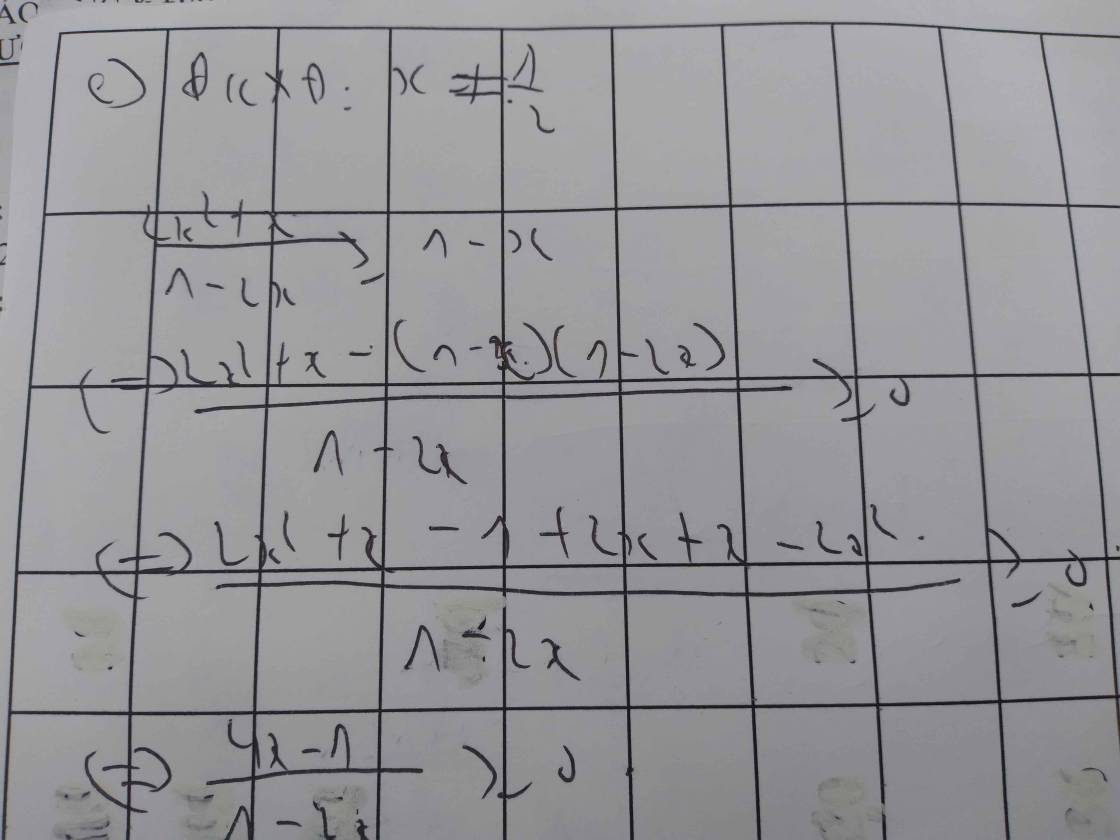
d) \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
\(\Leftrightarrow\dfrac{2x-5}{3x+2}-\dfrac{3x+2}{2x-5}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5\right)^2-\left(3x+2\right)^2}{\left(3x+2\right)\left(2x-5\right)}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5+3x+2\right)\left(2x-5-3x-2\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
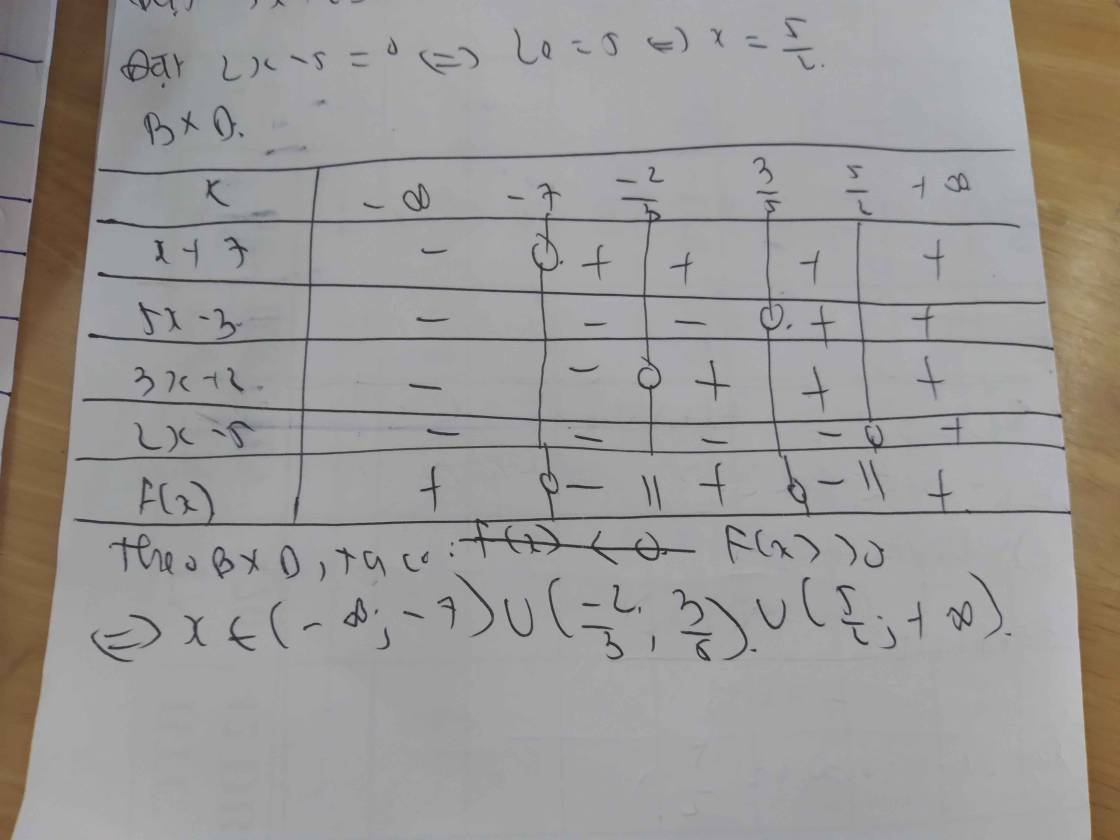
\(\Leftrightarrow\dfrac{-\left(5x-3\right)\left(x+7\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
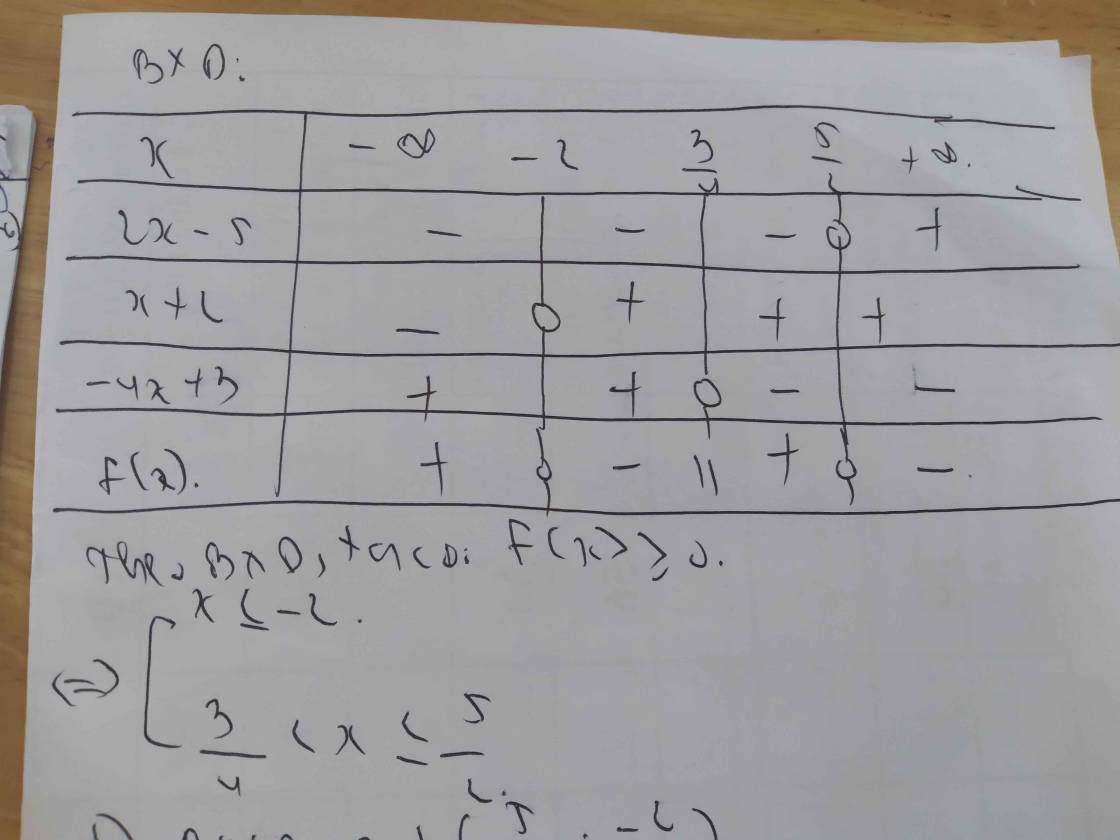
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-7< x< -\dfrac{2}{3}\\\dfrac{5}{3}< x< \dfrac{5}{2}\end{matrix}\right.\)