
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sửa đề: 8x-1
=>2(8x^2-x)(8x^2-x+2)-126=0
=>2[(8x^2-x)^2+2(8x^2-x)]-126=0
=>(8x^2-x)^2+2(8x^2-x)-63=0
=>(8x^2-x+9)(8x^2-x-7)=0
=>8x^2-x-7=0
=>x=1 hoặc x=-7/8

anh ơi, vậy là sai đề hả anh, chứ đề kêu chứng minh phương trình vô nghiệm mà em thấy anh ghi x=2

(x2 + x + 1)(6 - 2x) = 0
<=> 6 - 2x = 0 (do x2 + x + 1 > 0)
<=> 2x = 6
<=> x = 3
Vậy S = {3}
(8x - 4)(x2 + 2x + 2) = 0
<=> 8x - 4 = 0 (vì x2 + 2x + 2 > 0)
<=> 8x = 4
<=> x = 1/2
Vậy S = {1/2}
x3 - 7x + 6 = 0
<=> x3 - x - 6x + 6 = 0
<=> x(x2 - 1) - 6(x - 1) = 0
<=> x(x - 1)(x + 1) - 6(x - 1) = 0
<=> (x2 + x - 6)(x - 1) = 0
<=> (x2 + 3x - 2x - 6)(x - 1) = 0
<=> (x + 3)(x - 2)(x - 1) = 0
<=> x + 3 = 0
hoặc x - 2 = 0
hoặc x - 1 = 0
<=> x = -3
hoặc x = 2
hoặc x = 1
Vậy S = {-3; 1; 2}
x5 - 5x3 + 4x = 0
<=> x(x4 - 5x2 + 4) = 0
<=> x(x4 - x2 - 4x2 + 4) = 0
<=> x[x2(x2 - 1) - 4(x2 - 1)] = 0
<=> x(x - 2)(x + 2)(x - 1)(x + 1) = 0
<=> x = 0 hoặc x - 2 = 0 hoặc x + 2 = 0 hoặc x - 1 = 0 hoặc x + 1 = 0
<=> x = 0 hoặc x = 2 hoặc x = -2 hoặc x = 1 hoặc x = -1
Vậy S = {-2; -1; 0; 1; 2}
+ Ta có: \(\left(x^2+x+1\right).\left(6-2x\right)=0\)
- Ta lại có: \(x^2+x+1=\left(x^2+x+\frac{1}{4}\right)+\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\forall x\)
- Vì \(x^2+x+1>0\forall x\)mà \(\left(x^2+x+1\right).\left(6-2x\right)=0\)
\(\Rightarrow6-2x=0\Leftrightarrow-2x=-6\Leftrightarrow x=3\left(TM\right)\)
Vậy \(S=\left\{3\right\}\)
+ Ta có: \(\left(8x-4\right).\left(x^2+2x+2\right)=0\)
- Ta lại có: \(x^2+2x+2=\left(x^2+2x+1\right)+1=\left(x+1\right)^2+1\ge1>0\forall x\)
- Vì \(x^2+2x+2>0\forall x\)mà \(\left(8x-4\right).\left(x^2+2x+2\right)=0\)
\(\Rightarrow8x-4=0\Leftrightarrow8x=4\Leftrightarrow x=\frac{1}{2}\left(TM\right)\)
Vậy \(S=\left\{\frac{1}{2}\right\}\)
+ Ta có: \(x^3-7x+6=0\)
\(\Leftrightarrow\left(x^3-x^2\right)+\left(x^2-x\right)+\left(6x-6\right)=0\)
\(\Leftrightarrow x^2.\left(x-1\right)+x.\left(x-1\right)-6.\left(x-1\right)=0\)\(\Leftrightarrow\left(x-1\right).\left(x^2+x-6\right)=0\)
\(\Leftrightarrow\left(x-1\right).\left[\left(x^2-2x\right)+\left(3x-6\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right).\left[x.\left(x-2\right)+3.\left(x-2\right)\right]=0\)\(\Leftrightarrow\left(x-1\right).\left(x-2\right).\left(x+3\right)=0\)
\(\Leftrightarrow x=1\left(TM\right)\)hoặc \(x=2\left(TM\right)\)hoặc \(x=-3\left(TM\right)\)Vậy \(S=\left\{-3;1;2\right\}\)
+ Ta có: \(x^5-5x^3+4x=0\)
\(\Leftrightarrow x.\left(x^4-5x^2+4\right)=0\)\(\Leftrightarrow x.\left[\left(x^4-x^2\right)-\left(4x^2-4\right)\right]=0\)
\(\Leftrightarrow x.\left[x^2.\left(x^2-1\right)-4.\left(x^2-1\right)\right]=0\)
\(\Leftrightarrow x.\left(x^2-1\right).\left(x^2-4\right)=0\)
\(\Leftrightarrow x=0\left(TM\right)\)
hoặc \(x^2-1=0\Leftrightarrow x^2=1\Leftrightarrow x=\pm1\left(TM\right)\)
hoặc \(x^2-4=0\Leftrightarrow x^2=4\Leftrightarrow x=\pm2\left(TM\right)\)
Vậy \(S=\left\{-2;-1;0;1;2\right\}\)
!!@@# ^_^ Chúc bạn hok tốt ^_^#@@!!

f. 5 – (x – 6) = 4(3 – 2x)
<=>5-x+6=12-8x
<=>7x=1
<=>x=\(\dfrac{1}{7}\)
g. 7 – (2x + 4) = – (x + 4)
<=>7-2x-4=-x-4
<=>x=7
h. 2x(x+2)\(^2\)−8x\(^2\)=2(x−2)(x\(^2\)+2x+4)
<=>\(2x\left(x^2+4x+4\right)-8x^2=2\left(x^3-8\right)\)
<=>\(2x^3+8x^2+8x-8x^2=2\left(x^3-8\right)\)
<=>\(2x^3+8x=2x^3-16\)
<=>\(8x=-16\)
<=>\(x=-2\)
i. (x−2\(^3\))+(3x−1)(3x+1)=(x+1)\(^3\)
<=>\(x-8+9x^2-1=x^3+3x^2+3x+1\)
<=>\(6x^2-2x-10=0\)
<=>\(3x^2-x-5=0\)
<=>\(\left[{}\begin{matrix}x=\dfrac{1+\sqrt{61}}{6}\\x=\dfrac{1-\sqrt{61}}{6}\end{matrix}\right.\)
k. (x + 1)(2x – 3) = (2x – 1)(x + 5)
<=>\(2x^2-x-3=2x^2+9x-5\)
<=>10x=2
<=>\(x=\dfrac{1}{5}\)
f. 5 – (x – 6) = 4(3 – 2x)
<=>5-x+6=12-8x
<=>7x=1
<=>x=\(\dfrac{1}{7}\)
g. 7 – (2x + 4) = – (x + 4)
<=>7-2x-4=-x-4
<=>x=7
h. \(2x\left(x+2\right)^2-8x^2=2\left(x-2\right)\left(x^2+2x+4\right)\)
<=>\(2x\left(x^2+4x+4\right)-8x^2=2\left(x^3-8\right)\)
<=>\(2x^3+8x^2+8x-8x^2=2x^3-16\)
<=>\(8x=-16\)
<=>x=-2
i.\(\left(x-2\right)^3+\left(3x-1\right)\left(3x+1\right)=\left(x+1\right)^3\)
<=>\(x^3-6x^2+12x+8+9x^2-1=x^3+3x^2+3x+1\)
<=>\(9x+6=0\)
<=>x=\(\dfrac{-2}{3}\)
k. (x + 1)(2x – 3) = (2x – 1)(x + 5)
<=>\(2x^2-x-3=2x^2+9x-5\)
<=>10x=2
<=>x=\(\dfrac{1}{5}\)

\(1,\) thiếu đề
\(2,\dfrac{5x+2}{6}-\dfrac{8x-1}{3}=\dfrac{4x+2}{5}-5\)
\(\Leftrightarrow\dfrac{5\left(5x+2\right)}{30}-\dfrac{10\left(8x-1\right)}{30}=\dfrac{6\left(4x+2\right)}{30}-\dfrac{150}{30}\)
\(\Leftrightarrow5\left(5x+2\right)-10\left(8x-1\right)=6\left(4x+2\right)-150\)
\(\Leftrightarrow25x+10-80x+10=24x+12-150\)
\(\Leftrightarrow-55x+20=24x-138\)
\(\Leftrightarrow24x-138+55x-20=0\)
\(\Leftrightarrow79x-158=0\)
\(\Leftrightarrow x=2\)
\(3,ĐKXĐ:\left\{{}\begin{matrix}x\ne1\\x\ne-1\\x\ne3\end{matrix}\right.\\ \dfrac{x}{2x-6}+\dfrac{x}{2x-2}=\dfrac{-2x}{\left(x+1\right)\left(3-x\right)}\)
\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x-1\right)}+\dfrac{2x}{\left(x+1\right)\left(3-x\right)}=0\)
\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x-1\right)}-\dfrac{2x}{\left(x+1\right)\left(x-3\right)}=0\)
\(\Leftrightarrow x\left(\dfrac{1}{2\left(x-3\right)}+\dfrac{1}{2\left(x-1\right)}-\dfrac{2}{\left(x+1\right)\left(x-3\right)}\right)=0\)
\(\Leftrightarrow x\left(\dfrac{\left(x-1\right)\left(x+1\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}+\dfrac{\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}-\dfrac{4\left(x-1\right)}{2\left(x+1\right)\left(x-3\right)\left(x-1\right)}\right)=0\)
\(\Leftrightarrow x\left(\dfrac{x^2-1}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}+\dfrac{x^2-2x-3}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}-\dfrac{4x-4}{2\left(x+1\right)\left(x-3\right)\left(x-1\right)}\right)=0\)
\(\Leftrightarrow x.\dfrac{x^2-1+x^2-2x-3-4x+4}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x.\dfrac{2x^2-6x}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x.\dfrac{2x\left(x-3\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x.\dfrac{x}{\left(x-1\right)\left(x+1\right)}=0\)
\(\Leftrightarrow\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x=0\)

`a,(x+3)(x^2+2021)=0`
`x^2+2021>=2021>0`
`=>x+3=0`
`=>x=-3`
`2,x(x-3)+3(x-3)=0`
`=>(x-3)(x+3)=0`
`=>x=+-3`
`b,x^2-9+(x+3)(3-2x)=0`
`=>(x-3)(x+3)+(x+3)(3-2x)=0`
`=>(x+3)(-x)=0`
`=>` $\left[ \begin{array}{l}x=0\\x=-3\end{array} \right.$
`d,3x^2+3x=0`
`=>3x(x+1)=0`
`=>` $\left[ \begin{array}{l}x=0\\x=-1\end{array} \right.$
`e,x^2-4x+4=4`
`=>x^2-4x=0`
`=>x(x-4)=0`
`=>` $\left[ \begin{array}{l}x=0\\x=4\end{array} \right.$
1) a) \(\left(x+3\right).\left(x^2+2021\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\x^2+2021=0\end{matrix}\right.\\\left[{}\begin{matrix}x=-3\left(nhận\right)\\x^2=-2021\left(loại\right)\end{matrix}\right. \)
=> S={-3}

a, \(\left(x^2+x\right)^2+4\left(x^2+x\right)-12=0\)
\(\Leftrightarrow x^4+2x^3+x^2+4x^2+4x+12=0\)
\(\Leftrightarrow x^4+2x^3+5x^2+4x-12=0\)
\(\Leftrightarrow x^4-x^3+3x^3-3x^2+8x^2-8x+12x-12=0\)
\(\Leftrightarrow x^3\left(x-1\right)+3x^2\left(x-1\right)+8x\left(x-1\right)+12\left(x-1\right)=0\)
\(\Leftrightarrow\left(x^3+3x^2+8x+12\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left(x^3+2x^2+x^2+2x+6x+12\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[x^2\left(x+2\right)+x\left(x+2\right)+6\left(x+2\right)\right]\left(x-1\right)=0\)
\(\Leftrightarrow\left(x^2+x+6\right)\left(x+2\right)\left(x-1\right)=0\)
có : \(x^2+x+6>0\)
\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=1\end{cases}}}\)
b, \(\left(x-1\right)\left(x-3\right)\left(x+5\right)\left(x+7\right)-297=0\)
\(\Leftrightarrow\left[\left(x-1\right)\left(x+5\right)\right]\left[\left(x-3\right)\left(x+7\right)\right]-297=0\)
\(\Leftrightarrow\left(x^2+4x-5\right)\left(x^2+7x-21\right)-297=0\)
đặt \(x^2+4x-13=t\)
\(\Leftrightarrow\left(t+8\right)\left(t-8\right)-297=0\)
\(\Leftrightarrow t^2-64-297=0\)
\(\Leftrightarrow t^2=361\)
\(\Leftrightarrow t=\pm19\)
có t rồi tìm x thôi

a: =>10x-4=15-9x
=>19x=19
hay x=1
b: \(\Leftrightarrow3\left(10x+3\right)=36+4\left(8x+6\right)\)
=>30x+9=36+32x+24
=>30x-32x=60-9
=>-2x=51
hay x=-51/2
c: \(\Leftrightarrow2x+\dfrac{6}{5}=5-\dfrac{13}{5}-x\)
=>3x=6/5
hay x=2/5
d: \(\Leftrightarrow\dfrac{7x}{8}-\dfrac{5\left(x-9\right)}{1}=\dfrac{20x+1.5}{6}\)
\(\Leftrightarrow21x-120\left(x-9\right)=4\left(20x+1.5\right)\)
=>21x-120x+1080=80x+60
=>-179x=-1020
hay x=1020/179
e: \(\Leftrightarrow5\left(7x-1\right)+60x=6\left(16-x\right)\)
=>35x-5+60x=96-6x
=>95x+6x=96+5
=>x=1
f: \(\Leftrightarrow6\left(x+4\right)+30\left(-x+4\right)=10x-15\left(x-2\right)\)
=>6x+24-30x+120=10x-15x+30
=>-24x+96=-5x+30
=>-19x=-66
hay x=66/19

\(\left(x^2+8x\right)+8\left(x^2+8x\right)=48\)
Đặt: \(u=x^2+8x\)
\(\Rightarrow u^2+8u=48\)
\(\Leftrightarrow u^2+8u-48=0\)
\(\Leftrightarrow u^2-4u+12u-48=0\)
\(\Leftrightarrow u\left(u-4\right)+12\left(u-4\right)=0\)
\(\Leftrightarrow\left(u+12\right)\left(u-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}u+12=0\Leftrightarrow u=-12\\u-4=0\Leftrightarrow u=4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2+8x=-12\\x^2+8x=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+8x+12=0\\x^2+8x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4+2\sqrt{5}\\x=-4-2\sqrt{5}\\x=-2\\x=-6\end{matrix}\right.\)
\(\Leftrightarrow x^4+16x^3+64x^2+8x^2+64x=48\\ \Leftrightarrow x^4+16x^3+72x^2+64x-48=0\\ \Leftrightarrow\left(x+2\right)\left(x+6\right)\left(x^2+8x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+2=0\\x+6=0\\x^2+8x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-6\\x=-4\pm2\sqrt{5}\end{matrix}\right.\)
Vậy...

3(x+5)(x+6)(x+7)=8(x+6)-48 (1)
Đặt x+6=t
(1) <=> 3t(t-1)(t+1)=8t-48
<=> 3t3-11t+48=0
<=> (x+3)(3x2-9x+16) =0
Từ sau tự làm đi nghại ghi
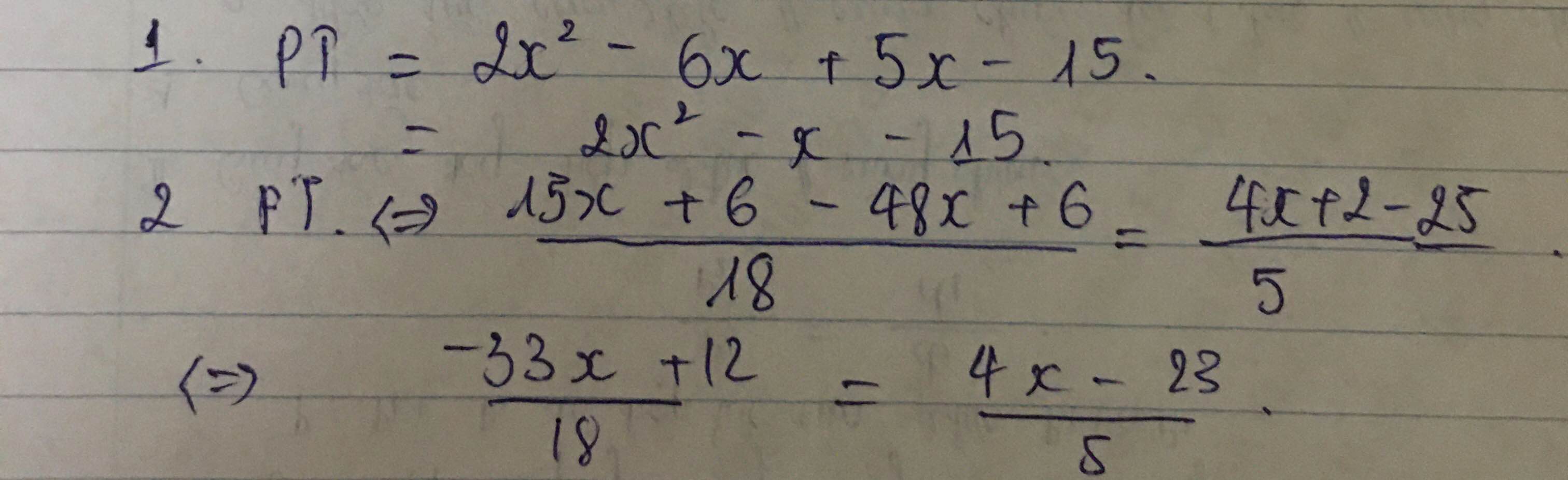
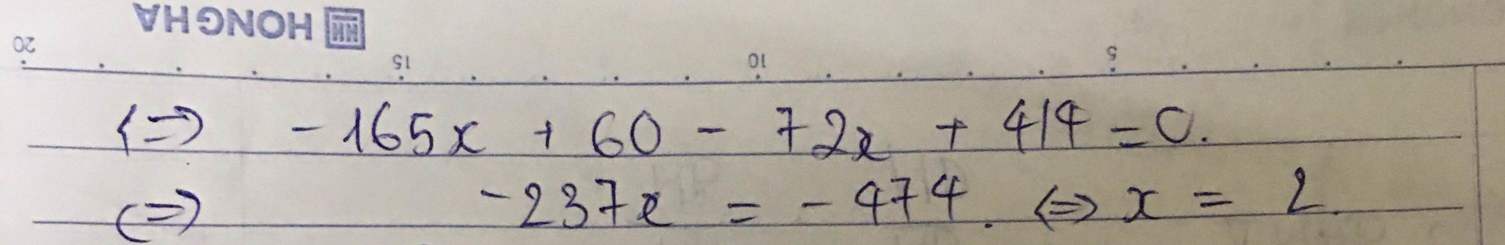
( x - 1 )( x + 6 )( x2 + 8x + 12 ) = 0
<=> ( x - 1 )( x + 6 )( x2 + 2x + 6x + 12 ) = 0
<=> ( x - 1 )( x + 6 )[ x( x + 2 ) + 6( x + 2 ) ] = 0
<=> ( x - 1 )( x + 6 )2( x + 2 ) = 0
<=> x = 1 hoặc x = -6 hoặc x = -2
Vậy ...
\(\left(x-1\right)\left(x+6\right)\left(x^2+8x+12\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+6\right)\left(x^2+2x+6x+12\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+6\right)\left[x.\left(x+2\right)+6.\left(x+2\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+6\right)\left(x+2\right)\left(x+6\right)=0\)
\(\Leftrightarrow x-1=0\)hoặc \(x+6=0\)hoặc \(x+2=0\)
\(\Leftrightarrow x=1\)hoặc \(x=-6\)hoặc \(x=-2\)
Vậy tập nghiêm của phương trình là \(S=\left\{1;-6;-2\right\}\)