Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Trong bài này ta áp dụng công thức tinh số hạng tổng quát un = u1.qn-1, biết hai đại lượng, ta sẽ tìm đại lượng còn lại:
a) q = 3.
b) u1 =
c) Theo đề bài ta có un = 192, từ đó ta tìm được n. Đáp số: n =7
a)
\(\dfrac{u_6}{u_1}=q^5=\dfrac{486}{2}=243=3^5\) . Suy ra: \(q=3\).
b)
\(u_4=u_1q^3=u_1.\left(\dfrac{2}{3}\right)^3=\dfrac{8}{21}\)\(\Rightarrow u_1=\dfrac{9}{7}\).
c) \(u_n=3.\left(-2\right)^{n-1}=192\)\(\Leftrightarrow\left(-2\right)^{n-1}=64=\left(-2\right)^6\)\(\Leftrightarrow n-1=6\)\(\Leftrightarrow n=7\).
Vậy số hạng thứ 7 bằng 192.
À cái kết luận đó liên quan tới lý thuyết đồ thị của các hàm bậc 3 mà lên lớp 12 mới học nên bạn thấy hơi lạ là đúng rồi :(
Bạn cứ hiểu hàm bậc 3 p(x) là một hàm mà miền giá trị của nó luôn chạy từ \(\left(-\infty;+\infty\right)\) bất chấp các hệ số A, B, C, D bằng bao nhiêu, do đó luôn chọn được 1 giá trị x nào đó sao p(x) nằm trên miền dương.
Đồng thời khi A<0 thì ta có \(\lim\limits_{x\rightarrow+\infty}p\left(x\right)=-\infty\) nên luôn tồn tại 1 giá trị x đủ lớn làm cho p(x) âm.
Hay bạn cứ nghĩ đơn giản cho A, B, C, D các giá trị bất kì trong đó A<0, rồi cho x một giá trị lớn cỡ vài tỉ thì kiểu gì p(x) cũng âm
Bạn cần ghi đầy đủ bài toán, ghi thiếu thế này thì chịu thua thôi bạn ạ
a) cosx - √3sinx = √2 ⇔ cosx - tan
sinx = √2
⇔ coscosx - sinsinx = √2cos ⇔ cos(x + ) = 
⇔ 
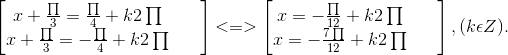
b) 3sin3x - 4cos3x = 5 ⇔ 
sin3x - 
cos3x = 1.
Đặt α = arccos thì phương trình trở thành
cosαsin3x - sinαcos3x = 1 ⇔ sin(3x - α) = 1 ⇔ 3x - α = 
+ k2π
⇔ x = 
, k ∈ Z (trong đó α = arccos).
\(f\left(x\right)=ax^3+bx^2+cx+d\)
a,b,c,d lập thành cấp số nhân công bội q \(\Rightarrow\left\{{}\begin{matrix}q\ne\left\{0,1\right\}\\a\ne0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=a.q\\c=aq^2\\d=aq^3\end{matrix}\right.\)
\(f\left(x\right)=a.x^3+a.q.x^2+a.q^2.x+a.q^3\)(1)
\(f\left(x\right)=a\left[.x^3+q.x^2+q^2.x+q^3\right]\)
\(f\left(x\right)=a.\left[.x^2\left(x+q\right)+q^2\left(.x+q\right)\right]\)
\(f\left(x\right)=a.\left(x+q\right)\left(x^2+q^2\right)\)
\(\left\{{}\begin{matrix}a,q\ne0\\f\left(x\right)=0\end{matrix}\right.\)\(\Rightarrow x=-q\) là nghiệm duy nhất