HA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TM
0
NT
0
CM
29 tháng 8 2017
b) x.(x+1). ( x+ 4). (x+ 5) = 12
⇔ [ x. (x + 5)]. [(x+1). (x+ 4)] = 12
⇔ x 2 + 5 x ⋅ x 2 + 4 x + x + 4 − 12 = 0 ⇔ x 2 + 5 x ⋅ x 2 + 5 x + 4 − 12 = 0 ( * )
Đặt t = x 2 + 5 x + 2
= > x 2 + 5 x = t – 2 v à x 2 + 5 x + 4 = t + 2
Khi đó phương trình (*) trở thành:
( t – 2). (t+ 2) - 12 = 0
⇔ t 2 − 4 − 12 = 0 ⇔ t 2 − 16 = 0 ⇔ t 2 = 16 ⇔ t = ± 4
+ Với t = 4 ta có: x 2 + 5 x + 2 = 4
⇔ x 2 + 5 x – 2 = 0 ( * * )
Có a= 1, b = 5, c = - 2 và ∆ = 5 2 – 4 . 1 . ( - 2 ) = 33 > 0
Nên (**) có 2 nghiệm phân biệt là:
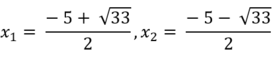
* Với t = - 4 ta có: x 2 + 5 x + 2 = - 4
⇔ x 2 + 5 x + 6 = 0 ( * * * )
Có a= 1, b = 5, c= 6 và ∆ = 5 2 – 4 . 1 . 6 = 1 > 0
Phương trình (***) có 2 nghiệm là:
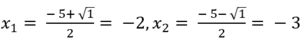
Vậy tập nghiệm của phương trình đã cho là:
CM
24 tháng 7 2018
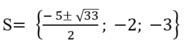
b) x.(x+1). ( x+ 4). (x+ 5) = 12
⇔ [ x. (x + 5)]. [(x+1). (x+ 4)] = 12
⇔ x 2 + 5 x ⋅ x 2 + 4 x + x + 4 − 12 = 0 ⇔ x 2 + 5 x ⋅ x 2 + 5 x + 4 − 12 = 0 ( * )
Đặt t = x 2 + 5 x + 2
= > x 2 + 5 x = t – 2 v à x 2 + 5 x + 4 = t + 2
Khi đó phương trình (*) trở thành:
( t – 2). (t+ 2) - 12 = 0
⇔ t 2 - 4 - 12 = 0 ⇔ t 2 - 16 = 0 ⇔ t 2 = 16 ⇔ t = ± 4
+ Với t = 4 ta có: x 2 + 5 x + 2 = 4
⇔ x2 +5x – 2 = 0 (**)
Có a= 1, b = 5, c = - 2 và ∆ = 5 2 – 4 . 1 . ( - 2 ) = 33 > 0
Nên (**) có 2 nghiệm phân biệt là:
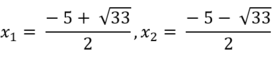
* Với t = - 4 ta có: x 2 + 5 x + 2 = - 4
⇔ x 2 + 5 x + 6 = 0 ( * * * )
Có a= 1, b = 5, c= 6 và ∆ = 5 2 – 4 . 1 . 6 = 1 > 0
Phương trình (***) có 2 nghiệm là:
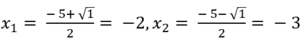
Vậy tập nghiệm của phương trình đã cho là:
14 tháng 5 2021
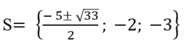
`1)(x+2)(x+3)(x-7)(x-8)=144`
`<=>[(x+2)(x-7)][(x+3)(x-8)]=144`
`<=>(x^2-5x-14)(x^2-5x-24)=144`
`<=>(x^2-5x-19)^2-25=144`
`<=>(x^2-5x-19)^2-169=0`
`<=>(x^2-5x-6)(x^2-5x-32)=0`
`+)x^2-5x-6=0`
`<=>` $\left[ \begin{array}{l}x=6\\x=-1\end{array} \right.$
`+)x^2-5x-32=0`
`<=>` $\left[ \begin{array}{l}x=\dfrac{5+3\sqrt{17}}{2}\\x=\dfrac{5-3\sqrt{17}}{2}\end{array} \right.$
Vậy `S={-1,6,\frac{5+3\sqrt{17}}{2},\frac{5-3\sqrt{17}}{2}}`
14 tháng 5 2021
1: Ta có: \(\left(x+2\right)\left(x+3\right)\left(x-7\right)\left(x-8\right)=144\)
\(\Leftrightarrow\left(x^2-7x+2x-14\right)\left(x^2-8x+3x-24\right)=144\)
\(\Leftrightarrow\left(x^2-5x-14\right)\left(x^2-5x-24\right)-144=0\)
\(\Leftrightarrow\left(x^2-5x\right)^2-38\left(x^2-5x\right)+336-144=0\)
\(\Leftrightarrow\left(x^2-5x\right)^2-38\left(x^2-5x\right)+192=0\)
\(\Leftrightarrow\left(x^2-5x\right)^2-6\left(x^2-5x\right)-32\left(x^2-5x\right)+192=0\)
\(\Leftrightarrow\left(x^2-5x\right)\left(x^2-5x-6\right)-32\left(x^2-5x-6\right)=0\)
\(\Leftrightarrow\left(x^2-5x-6\right)\left(x^2-5x-32\right)=0\)
\(\Leftrightarrow\left(x-6\right)\left(x+1\right)\left(x^2-5x-32\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-6=0\\x+1=0\\x^2-5x-32=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-1\\x=\dfrac{5-3\sqrt{17}}{2}\\x=\dfrac{5+3\sqrt{17}}{2}\end{matrix}\right.\)
Vậy: \(S=\left\{6;-1;\dfrac{5-3\sqrt{17}}{2};\dfrac{5+3\sqrt{17}}{2}\right\}\)
PL
0
QA
0
HP
2
6 tháng 1 2017
\(\sqrt{x^2+12}-\sqrt{x^2+5}=3x-5\)
\(\Leftrightarrow\left(\sqrt{x^2+12}+\left(x-6\right)\right)-\left(\left(x-5\right)+\sqrt{x^2+5}\right)+\left(-3x+6\right)=0\)
\(\Leftrightarrow\frac{12\left(x-2\right)}{\sqrt{x^2+12}+6-x}+\frac{10\left(x-2\right)}{\sqrt{x^2+5}+5-x}+-3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(\frac{12}{\sqrt{x^2+12}+6-x}+\frac{10}{\sqrt{x^2+5}+5-x}-3\right)=0\)
\(\Leftrightarrow x=2\)
5 tháng 1 2017
Dùng lượng liên hiệp mà giải đi bạn.
Giải được nghiệm x = 2 đó
Xét x=0 ==> loại
Xét x\(\ne\)0,ta chia cả 2 vế cho x2 thu được:
4(x2+17x+60)(x2+16x+60)=3x2
4(x+\(\frac{60}{x}\)+17)(x+\(\frac{60}{x}\)+16)=3
Đặt x+\(\frac{60}{x}\)+16=t,ta được
4(t+1).t=3 <=> 4t2+4t-3=0 <=> t=\(\frac{1}{2}\)hoặc t=\(\frac{-3}{2}\)
Với t=1/2,ta có x+\(\frac{60}{x}\)+16=1/2 <=> x=-15/2 hoặc x=-8
Với t=-3/2,ta có x+\(\frac{60}{x}\)+16=-3/2 <=> ... bạn tự giải nốt nhé.