Giải Phương Trình :3x2 + 2x - 34 + 2/x + 3/x2 = 0

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

DS

đặng sĩ nguyên

15 tháng 9 2021 - olm

Giải Phương Trình :

3x2 + 2x - 34 + 2/x + 3/x2 = 0

#Hỏi cộng đồng OLM #Toán lớp 9

1

PT

Phạm Tuấn Minh

15 tháng 9 2021

Tính theo mẫu

Các câu hỏi dưới đây có thể giống với câu hỏi trên

NC

Nii-chan

10 tháng 1 2021

Giải phương trình :

1) √x²+x+2 + 1/x= 13-7x/2

2) x² + 3x = √1-x + 1/4

3) ( x+3)√48-x²-8x= 28-x/ x+3

4) √-x²-2x +48= 28-x/x+3

5) 3x² + 2(x-1)√2x²-3x +1= 5x + 2

6) 4x² +(8x - 4)√x -1 = 3x+2√2x² +5x-3

7) x³/ √16-x² + x² -16 = 0

#Hỏi cộng đồng OLM #Toán lớp 9

0

PT

Pham Trong Bach

2 tháng 7 2017

Giải phương trình bằng cách đưa về phương trình tích: a ) 3 x 2 − 7 x − 10 ⋅ 2 x ...

Giải phương trình bằng cách đưa về phương trình tích:

a ) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0 b ) x 3 + 3 x 2 − 2 x − 6 = 0 c ) x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x d ) x 2 + 2 x − 5 2 = x 2 − x + 5 2

#Hỏi cộng đồng OLM #Toán lớp 9

1

CM

Cao Minh Tâm

2 tháng 7 2017

a) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0

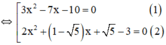
Giải bài 39 trang 57 SGK Toán 9 Tập 2 | Giải toán lớp 9

+ Giải (1):

3 x 2 – 7 x – 10 = 0

Có a = 3; b = -7; c = -10

⇒ a – b + c = 0

⇒ (1) có hai nghiệm x 1 = - 1 v à x 2 = - c / a = 10 / 3 .

+ Giải (2):

2 x 2 + ( 1 - √ 5 ) x + √ 5 - 3 = 0

Có a = 2; b = 1 - √5; c = √5 - 3

⇒ a + b + c = 0

⇒ (2) có hai nghiệm:

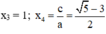
Giải bài 39 trang 57 SGK Toán 9 Tập 2 | Giải toán lớp 9

Vậy phương trình có tập nghiệm 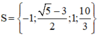Giải bài 39 trang 57 SGK Toán 9 Tập 2 | Giải toán lớp 9

b)

x 3 + 3 x 2 - 2 x - 6 = 0 ⇔ x 3 + 3 x 2 - ( 2 x + 6 ) = 0 ⇔ x 2 ( x + 3 ) - 2 ( x + 3 ) = 0 ⇔ x 2 - 2 ( x + 3 ) = 0

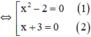
Giải bài 39 trang 57 SGK Toán 9 Tập 2 | Giải toán lớp 9

+ Giải (1): x 2 – 2 = 0 ⇔ x 2 = 2 ⇔ x = √2 hoặc x = -√2.

+ Giải (2): x + 3 = 0 ⇔ x = -3.

Vậy phương trình có tập nghiệm S = {-3; -√2; √2}

c)

x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x ⇔ x 2 − 1 ( 0 , 6 x + 1 ) = x ⋅ ( 0 , 6 x + 1 ) ⇔ x 2 − 1 ( 0 , 6 x + 1 ) − x ( 0 , 6 x + 1 ) = 0 ⇔ ( 0 , 6 x + 1 ) x 2 − 1 − x = 0

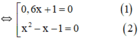
Giải bài 39 trang 57 SGK Toán 9 Tập 2 | Giải toán lớp 9

+ Giải (1): 0,6x + 1 = 0 ⇔ 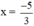Giải bài 39 trang 57 SGK Toán 9 Tập 2 | Giải toán lớp 9

+ Giải (2):

x 2 – x – 1 = 0

Có a = 1; b = -1; c = -1

⇒ Δ = ( - 1 ) 2 – 4 . 1 . ( - 1 ) = 5 > 0

⇒ (2) có hai nghiệm 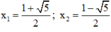Giải bài 39 trang 57 SGK Toán 9 Tập 2 | Giải toán lớp 9

Vậy phương trình có tập nghiệm 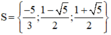Giải bài 39 trang 57 SGK Toán 9 Tập 2 | Giải toán lớp 9

d)

x 2 + 2 x − 5 2 = x 2 − x + 5 2 ⇔ x 2 + 2 x − 5 2 − x 2 − x + 5 2 = 0 ⇔ x 2 + 2 x − 5 − x 2 − x + 5 ⋅ x 2 + 2 x − 5 + x 2 − x + 5 = 0 ⇔ ( 3 x − 10 ) 2 x 2 + x = 0

⇔ (3x-10).x.(2x+1)=0

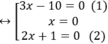
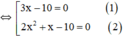
Giải bài 39 trang 57 SGK Toán 9 Tập 2 | Giải toán lớp 9

Giải bài 39 trang 57 SGK Toán 9 Tập 2 | Giải toán lớp 9

+ Giải (1): 3x – 10 = 0 ⇔ 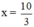Giải bài 39 trang 57 SGK Toán 9 Tập 2 | Giải toán lớp 9

+ Giải (2):

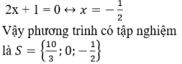
Giải bài 39 trang 57 SGK Toán 9 Tập 2 | Giải toán lớp 9

NT

Nguyễn Thanh Vân

26 tháng 4 2020 - olm

a ) Giải hệ pt:

\(2x^4+3x^2-2=0\)

b ) Cho phương trình x2 - (m+1)x +m =0 . tìm tất cả các giá trị của tham số m để phương trình có hai nghiệm phân biệt x1, x2 thoă mãn x1 = 3x2

#Hỏi cộng đồng OLM #Toán lớp 9

2

NH

Nguyễn Hoàng Bảo Nhi

27 tháng 4 2020

Câu a )

\(2x^4+3x^2-2=0\left(1\right)\)

Đặt \(t=x^2\left(t\ge0\right)\) phương trình (1) trở thành:

\(2t^2+3t-2=0\)

\(\Leftrightarrow t\left(2t-1\right)+4t-2=0\)

\(\Leftrightarrow t\left(2t-1\right)+2\left(2t-1\right)=0\)

\(\Leftrightarrow\left(2t-1\right)\left(t+2\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}2t-1=0\\t+2=0\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}t=\frac{1}{2}\\1=-2\left(loại\right)\end{cases}}\)

Với \(t=\frac{1}{2}\Leftrightarrow x^2=\frac{1}{2}\Rightarrow x=\pm\frac{\sqrt{2}}{2}\)

Vậy tập nghiệm của phương trình là \(S=\left\{\pm\frac{\sqrt{2}}{2}\right\}\)

NH

Nguyễn Hoàng Bảo Nhi

27 tháng 4 2020

Câu b )

\(\Delta=\left(m+1\right)^2-4m=m^2-2m+1=\left(m-1\right)^2\)

\(\Delta>0\Leftrightarrow\left(m-1\right)^2>0\Leftrightarrow m\ne1\)

\(\hept{\begin{cases}x_1+x_2=m+1\\x_1x_2=m\end{cases}}\)

\(x_1=3x_2\Rightarrow3x_2+x_2=m+1\Leftrightarrow4x_2=m+1\)

\(\Leftrightarrow x_2=\frac{m+1}{4}\Rightarrow x_1=\frac{3\left(m+1\right)}{4}\)

\(x_1x_2=m\Leftrightarrow\frac{3\left(m+1\right)^2}{16}=m\)

\(\Leftrightarrow3m^2+6m+3=16m\)

\(\Leftrightarrow3m^2-10m+3=0\)

\(\Leftrightarrow\left(3m-1\right)\left(m-3\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}m=\frac{1}{3}\\m=3\end{cases}\left(tm\right)}\)

VV

Vũ Vếu

17 tháng 5 2023

Câu 3. Cho phương trinh x ^ 2 - (2m - 1) * x - 8m = 0(1) ( m là tam số) a) Giải phương trình khi m=1 b) Tim m dễ phương trình có hai nghiệm phân biệt X1, X2 thoả mãn 3x1^2 + 3x2^2 + 2x₁X² = - 5

#Hỏi cộng đồng OLM #Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

17 tháng 5 2023

a: Khi m=1 thì (1) sẽ là:

x^2-x-8=0

=>\(x=\dfrac{1\pm\sqrt{33}}{2}\)

b: 3x1^2+3x2^2+2x1x2=5

=>3[(x1+x2)^2-2x1x2]+2x1x2=5

=>3[(2m-1)^2-2(-8m)]+2(-8m)=5

=>3(4m^2-4m+1+16m)-16m=5

=>12m^2+36m+3-16m-5=0

=>12m^2+20m-2=0

=>\(m=\dfrac{-5\pm\sqrt{31}}{6}\)

PT

Pham Trong Bach

13 tháng 4 2017

Đưa các phương trình sau về dạng a x 2 + 2 b ' x + c = 0 và giải chúng. Sau đó, dùng bảng số hoặc máy tính để viết gần đúng nghiệm tìm được (làm tròn kết quả đến chữ số thập phân thứ hai): a ) ...

#Hỏi cộng đồng OLM #Toán lớp 9

1

CM

Cao Minh Tâm

13 tháng 4 2017

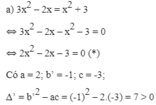
Phương trình (*) có hai nghiệm phân biệt:

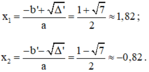
Giải bài 18 trang 49 SGK Toán 9 Tập 2 | Giải toán lớp 9

Có: a = 3; b’ = -2√2; c = 2;

Δ ’ = b ’ 2 – a c = ( - 2 √ 2 ) 2 – 3 . 2 = 2 > 0

Vì Δ’ > 0 nên phương trình có hai nghiệm phân biệt là:

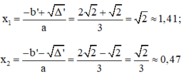
Giải bài 18 trang 49 SGK Toán 9 Tập 2 | Giải toán lớp 9

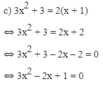
Phương trình có a = 3; b’ = -1; c = 1;

Δ ’ = b ’ 2 – a c = ( - 1 ) 2 – 3 . 1 = - 2 < 0

Vậy phương trình vô nghiệm.

d)

0 , 5 x ( x + 1 ) = ( x – 1 ) 2 ⇔ 0 , 5 x 2 + 0 , 5 x = x 2 – 2 x + 1 ⇔ x 2 – 2 x + 1 – 0 , 5 x 2 – 0 , 5 x = 0 ⇔ 0 , 5 x 2 – 2 , 5 x + 1 = 0 ⇔ x 2 – 5 x + 2 = 0

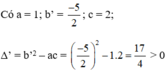
Giải bài 18 trang 49 SGK Toán 9 Tập 2 | Giải toán lớp 9

Phương trình có hai nghiệm phân biệt:

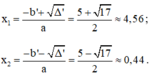
Giải bài 18 trang 49 SGK Toán 9 Tập 2 | Giải toán lớp 9

TT

Tri Truong

12 tháng 3 2022

Bài 3: Cho phương trình 3x2 –2x–2=0 có hai nghiệm x1 , x2 . Hãy tính giá trị của biểu thức: D=x1/x2-1 + x2/x1-1

#Hỏi cộng đồng OLM #Toán lớp 9

0

NN

Nguyễn nhật vũ

3 tháng 12 2021

cho phương trình x2+(m-3)x-m+1=0 A)tìm m để phương trình có 2 no x1,x2 sao cho P=x1x2-x21-x22 đạt giá trị lớn nhất B)tìm m để phương trình có 2no x1,x2 cho bt T=15/(x1-3x2)x1+x22 đạt giá trị lớn nhất 3x2 là x2 ko phải là mũ 2 ạ ở phần này ko có mũ 2 ạ X22 cái nào em viết trc là ở trên ạ Em cảm ơn ạ

#Hỏi cộng đồng OLM #Toán lớp 9

0

NT

Nguyễn Thị Ngọc Anh

5 tháng 2 2022

Bài 7: Giải phương trình : a)( x- 2x + 3 ) ( 2x - x+6 ) =18

b) 3x3 + 6x2 –4x = 0

c) 3x2 – 5x = 0

d) – 2x2 + 8 = 0

#Hỏi cộng đồng OLM #Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

5 tháng 2 2022

a: \(\Leftrightarrow\left(-x+3\right)\left(x+6\right)=18\)

\(\Leftrightarrow-x^2-6x+3x+18-18=0\)

\(\Leftrightarrow-x\left(x+3\right)=0\)

=>x=0 hoặc x=-3

b: \(\Leftrightarrow x\left(3x^2+6x-4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\3x^2+6x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2+2x-\dfrac{4}{3}=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\\left(x+1\right)^2=\dfrac{7}{3}\end{matrix}\right.\Leftrightarrow x\in\left\{0;\dfrac{\sqrt{21}}{3}-1;\dfrac{-\sqrt{21}}{3}-1\right\}\)

c: =>x(3x-5)=0

=>x=0 hoặc x=5/3

d: =>(x-2)(x+2)=0

=>x=2 hoặc x=-2

HN

Hoàng Nguyệt

13 tháng 5 2021

Phương trình: \(^{x^2-x-3=0}\) có 2 nghiệm x1,x2. Tính giá trị \(^{x1^3x2+x2^3x1=21}\)

#Hỏi cộng đồng OLM #Toán lớp 9

4

NV

Nguyễn Việt Lâm

Giáo viên

13 tháng 5 2021

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=-3\end{matrix}\right.\)

\(x_1^3x_2+x_2^3x_1=x_1x_2\left(x^2_1+x_2^2\right)=x_1x_2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\)

\(=-3.\left(1^2-2.\left(-3\right)\right)=-21\)

Y

Yeutoanhoc

13 tháng 5 2021

`Delta=1+12=13>0`
`=>` pt có 2 nghiệm pb
Áp dụng vi-ét:`x_1+x_2=1,x1.x_2=-3`
`=>x_1^3x_2+x_1x_2^3`
`==x_1.x_2(x_1^2+x_2)^2`
=-3[(x_1+x_2)^2-2.x_1.x_2]`
`=-3(1+6(`
`=-3.7`
`=-21`

BC

Bảo Châu Nguyễn

19 tháng 2 2023

Cho phương trình: \(x^2\)- 3x + m - 3 = 0. Tìm m để phương trình có 2 nghiệm x1, x2 thỏa mãn: \(x1^2\) + 3x2 = \(x1^2\)\(x2^2\) - 11

#Hỏi cộng đồng OLM #Toán lớp 9

0