
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


d) Phương trình đã cho tương đương với :
\(2^{3x}+2^x.3^{2x}=2.3^{2x}\Leftrightarrow\left(\frac{2}{3}\right)^{2x}+\left(\frac{2}{3}\right)^x-2=0\)
Đặt \(t=\left(\frac{2}{3}\right)^x,\left(t>0\right)\) Phương trình trở thành
\(t^3+t-2=0\) hay \(\left(t-1\right)\left(t^2+t+2\right)=0\)
Do \(t^2+t+2=\left(t+\frac{1}{2}\right)^2+\frac{7}{4}>0\) nên \(t-1=0\) hay t=1
Từ đó suy ra \(\left(\frac{2}{3}\right)^x=1=\left(\frac{2}{3}\right)^0\Leftrightarrow x=0\)
Vậy phương trình có nghiệm duy nhất \(x=0\)
c) Điều kiện \(x\ne0\). Chia cả 2 vế của phương trình cho \(6^{\frac{1}{x}}>0\), ta có :
\(6.\left(\frac{3}{2}\right)^{\frac{1}{x}}-13.1+6\left(\frac{2}{3}\right)^{\frac{1}{x}}=0\)
Đặt \(t=\left(\frac{3}{2}\right)^{\frac{1}{x}},\left(t>0\right)\)
Phương trình trở thành
\(6t-13+\frac{6}{t}=0\) hay \(6t^2-13t+6=0\)
Phương trình bậc 2 trên có 2 nghiệm dương \(t=\frac{3}{2},t=\frac{2}{3}\)
Với \(t=\frac{3}{2}\) thì \(\left(\frac{3}{2}\right)^{\frac{1}{x}}=\frac{3}{2}\Leftrightarrow\frac{1}{x}=1\Leftrightarrow x=1\)
Với \(t=\frac{2}{3}\) thì \(\left(\frac{3}{2}\right)^{\frac{1}{x}}=\frac{2}{3}\Leftrightarrow\frac{1}{x}=-1\Leftrightarrow x=-1\)

Đặt \(f\left(x\right)=\left(\frac{1}{6}\right)^x+2\left(\frac{1}{3}\right)^x+3\left(\frac{1}{2}\right)^x\)
Nhận thấy f(2) = 1. Mặt khác f(x) là tổng của các hàm số nghịch biến trên R. Do đó f(x) cũng là hàm nghịch biến. Từ đó ta có :
\(f\left(x\right)<1=f\left(2\right)\Leftrightarrow x>2\)
Vậy tập nghiệm của bất phương trình là
\(D=\left(2;+\infty\right)\)

a) Đặt t = 13x > 0 ta được phương trình:
13t2 – t – 12 = 0 ⇔ (t – 1)(13t + 12) = 0
⇔ t = 1 ⇔ 13x = 1 ⇔ x = 0
b)
Chia cả hai vế phương trình cho 9x ta được phương trình tương đương
(1+(23)x)(1+3.(23)x)=8.(23)x(1+(23)x)(1+3.(23)x)=8.(23)x
Đặt t=(23)xt=(23)x (t > 0) , ta được phương trình:
(1 + t)(1 + 3t) = 8t ⇔ 3t2 – 4t + 1 = 0 ⇔ t∈{13,1}t∈{13,1}
Với t=13t=13 ta được nghiệm x=log2313x=log2313
Với t = 1 ta được nghiệm x = 0
c) Điều kiện: x > 2
Vì nên phương trình đã cho tương đương với:
[log3(x−2)=0log5x=1⇔[x=3x=5[log3(x−2)=0log5x=1⇔[x=3x=5
d) Điều kiện: x > 0
log22x – 5log2x + 6 = 0
⇔(log2x – 2)(log2x – 3) = 0
⇔ x ∈ {4, 8}

a) Điều kiện: \(\left\{{}\begin{matrix}4x+2>0\\x-1>0\\x>0\end{matrix}\right.\)
Hay là: \(x>1\)
Khi đó biến đổi pương trình như sau:
\(\ln\dfrac{4x+2}{x-1}=\ln x\)
\(\Leftrightarrow\dfrac{4x+2}{x-1}=x\)
\(\Leftrightarrow4x+2=x\left(x-1\right)\)
\(\Leftrightarrow x^2-5x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{5+\sqrt{33}}{2}\\x_2=\dfrac{5-\sqrt{33}}{2}\left(loại\right)\end{matrix}\right.\)
Vậy nghiệm của phương trình là: \(x=\dfrac{5+\sqrt{33}}{2}\)
b) Điều kiện: \(\left\{{}\begin{matrix}3x+1>0\\x>0\end{matrix}\right.\)
Hay là: \(x>0\)
Biến đổi phương trình như sau:
\(\log_2\left(3x+1\right)\log_3x-2\log_2\left(3x+1\right)=0\)
\(\Leftrightarrow\log_2\left(3x+1\right)\left(\log_3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\log_2\left(3x+1\right)=0\\\log_3x=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+1=2^0\\x=3^2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=9\end{matrix}\right.\)
Vậy nghiệm là x = 9.


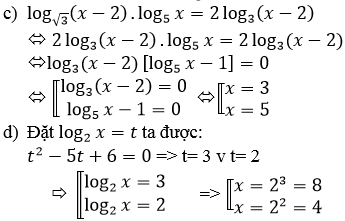
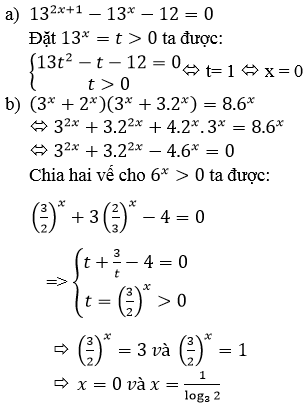





Đáp án C