K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 9 2021
\(\left(\dfrac{1}{16}\right)^{x+2}=\left(\dfrac{1}{32}\right)^6\)
\(\Leftrightarrow\dfrac{1}{16^{x+2}}=\dfrac{1}{32^6}\)
\(\Leftrightarrow\dfrac{1}{2^{4x+8}}=\dfrac{1}{2^{30}}\)
\(\Leftrightarrow4x+8=30\Leftrightarrow4x=22\Leftrightarrow x=\dfrac{11}{2}\)
10 tháng 9 2020
Bài làm :
\(\left(\frac{1}{16}\right)^{x+2}=\left(\frac{1}{32}\right)^6\)
\(\Rightarrow\left(\frac{1}{2^4}\right)^{x+2}=\left(\frac{1}{2^5}\right)^6\)
\(\Rightarrow\left(\frac{1}{2}\right)^{4x+8}=\left(\frac{1}{2}\right)^{30}\)
\(\Rightarrow4x+8=30\)
\(\Rightarrow4x=22\)
\(\Rightarrow x=\frac{11}{2}\)
Học tốt nhé
10 tháng 9 2020
\(\left(\frac{1}{16}\right)^{x+2}=\left(\frac{1}{32}\right)^6=>\left[\left(\frac{1}{2}\right)^4\right]^{x+2}=\left[\left(\frac{1}{2}\right)^4\right]^6\)
\(\left(\frac{1}{2}\right)^{4.\left(x+2\right)}=\left(\frac{1}{2}\right)^{30}\)
4.(x+2)=30
(x+2)=30:4
(x+2)=7,5
x=7,5+2
x=9,5
vậy x=9,5
17 tháng 6 2016
\(x^2=\frac{1}{16}=\left(\frac{1}{4}\right)^1=\left(-\frac{1}{4}\right)^2\)
Vậy có 2 ngiệm x
TH1: \(x=\frac{1}{4}\)
TH2: \(x=-\frac{1}{4}\)
17 tháng 6 2016
x2=1/16
=>x=1/4; x=-1/4
x5=(2/3)5
=>x=2/3
x4=(3/2)4
=>x=3/2; x=-3/2
PT
1
2 tháng 9 2016
Có: \(A=4\cdot\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\)
\(=\frac{1}{2}\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\)
\(=\frac{\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)}{2}\)
\(=...........................\)
\(=\frac{3^{32}-1}{2}\)
\(B=3^{32-1}\)
=> \(A< B\)
QM
1
H9
HT.Phong (9A5)
CTVHS
1 tháng 5 2023
Giá trị của biểu thức \(M=-2x^2.y^3-4xy^2\) tại x=1 và y=2 là:
\(M=-2x^2.y^3-4xy^2=-2.1^2.2^3-4.1.2^2=-32\)
⇒ Chọn B
17 tháng 9 2023
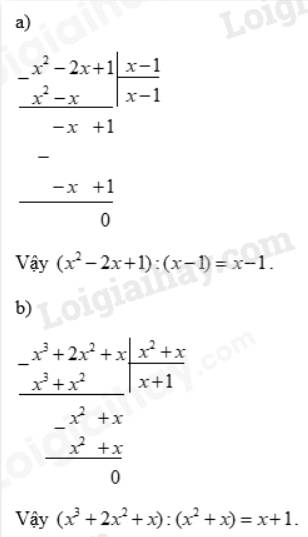
Vậy \(( - 32{x^5} + 1):( - 2x + 1) = 16{x^4} + 8{x^3} + 4{x^2} + 2x + 1\).
LN
0
19 tháng 7 2016
\(\frac{2^{4-x}}{16^5}=32^6\)
\(\Rightarrow\frac{2^{4-x}}{\left(2^4\right)^5}=\left(2^5\right)^6\)
\(\Rightarrow\frac{2^{4-x}}{2^{20}}=2^{30}\)
\(\Rightarrow2^{4-x}=2^{30}.2^{20}\)
\(\Rightarrow2^{4-x}=2^{50}\)
\(\Rightarrow4-x=50\)
\(\Rightarrow x=-46\)
\(\left(\dfrac{1}{16}\right)^x=\left(\dfrac{1}{32}\right)^{16}\\ =>\left[\left(\dfrac{1}{2}\right)^4\right]^x=\left[\left(\dfrac{1}{2}\right)^5\right]^{16}\\ =>\left(\dfrac{1}{2}\right)^{4\cdot x}=\left(\dfrac{1}{2}\right)^{5\cdot16}\\ =>\left(\dfrac{1}{2}\right)^{4x}=\left(\dfrac{1}{2}\right)^{80}\\ =>4x=80\\ =>x=\dfrac{80}{4}\\ =>x=20\)
Vậy: ..