K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
P
24 tháng 7 2023
`a)` `(5/7)^(2).(5/7)^(5).5/7`
`=(5/7)^(2+3+1)`
`=(5/7)^8`
`b)` `(3/7)^(2).(9)/(49)`
`=(3/7)^(2).(3/7)^(2)`
`=(3/7)^(2+2)`
`=(3/7)^4`
AD
24 tháng 7 2023
\(a,\left(\dfrac{5}{7}\right)^2.\left(\dfrac{5}{7}\right)^5.\dfrac{5}{7}=\left(\dfrac{5}{7}\right)^{2+5+1}=\left(\dfrac{5}{7}\right)^8\\ b,\left(\dfrac{3}{7}\right)^2.\dfrac{9}{49}=\left(\dfrac{3}{7}\right)^2.\left(\dfrac{3}{7}\right)^2=\left(\dfrac{3}{7}\right)^{2+2}=\left(\dfrac{3}{7}\right)^4\)
S
9 tháng 7 2018
12,7 - 17,2 + 199,9 - 22,8 - 149,9
= 12,7 - (17,2+22,8) + (199,9-149,9)
= 12,7 - 40 + 50
= 12,7 + 10 = 22,7
AD
24 tháng 7 2023
\(a,9.\left(\dfrac{1}{3}\right)^2+\left(\dfrac{1}{7}\right)^0-1\\ =9.\dfrac{1}{9}+1-1\\ =\dfrac{9}{9}+1-1\\ =1+1-1\\ =1\\ b,7.\left(5^2-5\right)+\left(-1\right)^2\\ =7.\left(25-5\right)+1\\ =7.20+1\\ =140+1\\ =141\)
H9
HT.Phong (9A5)
CTVHS
28 tháng 7 2023
a) \(x-\dfrac{1}{5}=\dfrac{-2}{15}\)
\(\Rightarrow x=\dfrac{-2}{15}+\dfrac{1}{5}\)
\(\Rightarrow x=\dfrac{-2}{15}+\dfrac{3}{15}\)
\(\Rightarrow x=\dfrac{1}{15}\)
b) \(8\cdot\left(3^2+1\right)-\dfrac{2}{7}\cdot7\)
\(=8\cdot\left(9+1\right)-\dfrac{2\cdot7}{7}\)
\(=8\cdot10-2\)
\(=80-2\)
\(=78\)
17 tháng 10 2021
Bài 5:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{9}=\dfrac{x-y}{10-9}=4\)
Do đó: x=40; y=36
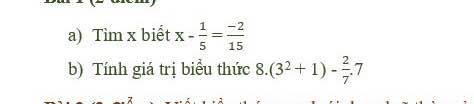
\(A=\dfrac{1}{9}xy^3.\left(-3x^2y\right)^2=\dfrac{1}{9}xy^3.9x^4y^2=x^5y^5.\)
\(\Rightarrow\) Hệ số: 1. Phần biến: x; y. Bậc: 5.
\(B=\left(\dfrac{3}{5}x^2y^2z\right).\left(\dfrac{-40}{9}xy^2z^2\right)=\dfrac{-8}{3}x^3y^4z^3.\)
\(\Rightarrow\) Hệ số: \(\dfrac{-8}{3}\). Phần biến: x; y; z. Bậc: 4.
\(M=\dfrac{-1}{5}x^3y^2.15x^2y^4=-3x^5y^6.\)
\(\Rightarrow\) Hệ số: -3. Phần biến: x; y. Bậc: 6.