
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,9.\left(\dfrac{1}{3}\right)^2+\left(\dfrac{1}{7}\right)^0-1\\ =9.\dfrac{1}{9}+1-1\\ =\dfrac{9}{9}+1-1\\ =1+1-1\\ =1\\ b,7.\left(5^2-5\right)+\left(-1\right)^2\\ =7.\left(25-5\right)+1\\ =7.20+1\\ =140+1\\ =141\)

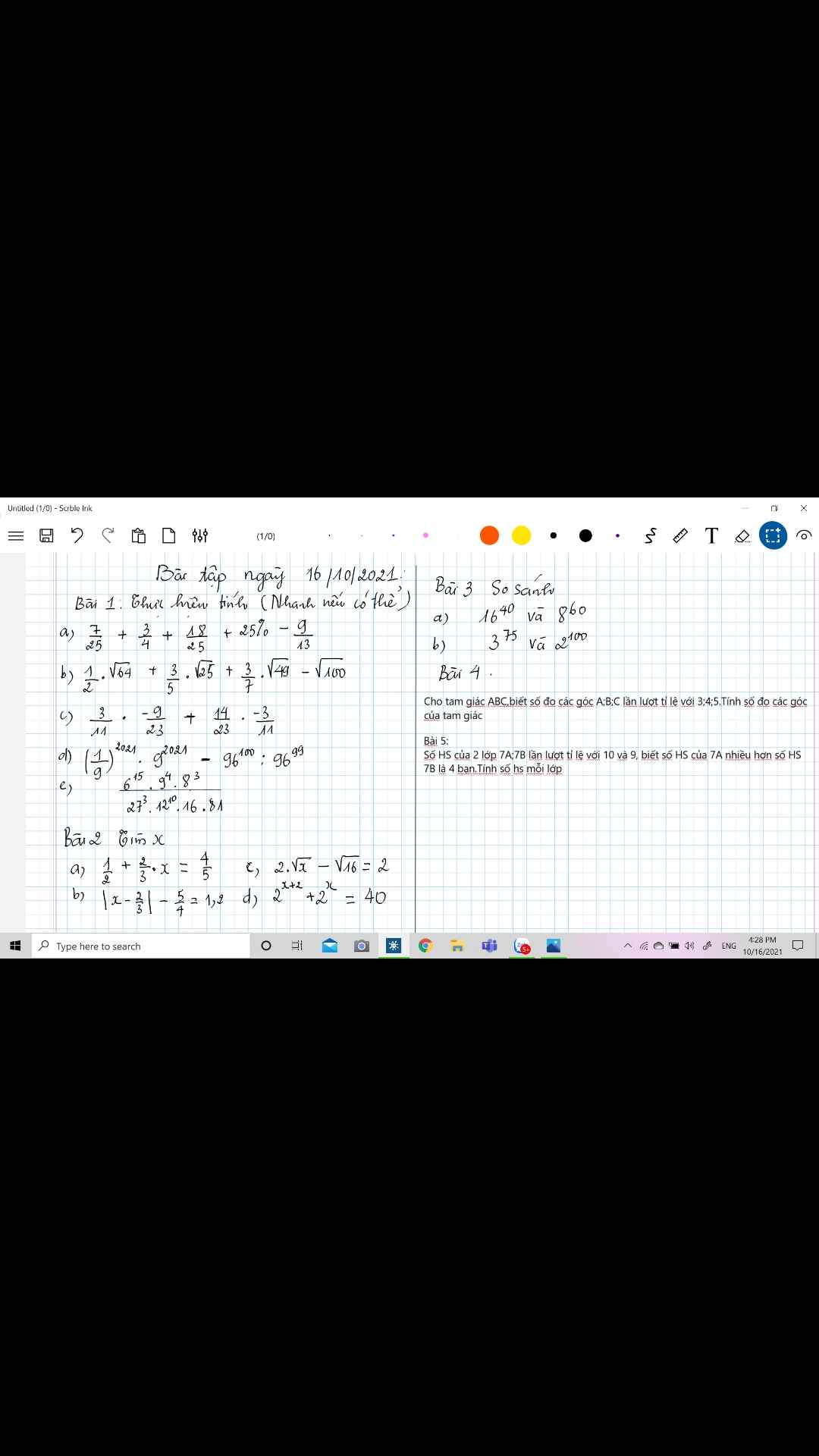
Bài 5:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{9}=\dfrac{x-y}{10-9}=4\)
Do đó: x=40; y=36

\(B=\left|2x+3,5\right|+\left|2x+\frac{7}{2}\right|\)
\(=\left|3,5-2x\right|+\left|2x+3,5\right|\ge\left|3,5-2x+2x+3,5\right|=7\)
Dấu '' = '' xảy ra khi \(\left(3,5-2x\right)\left(2x+3,5\right)\ge0\)
\(\Rightarrow\orbr{\begin{cases}3,5-2x\ge0;2x+3,5\ge0\\3,5-2x\le0;2x+3,5\le0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}2x\le3,5;2x\ge-3,5\\2x\ge3,5;2x\le-3,5\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x\le1,75;x\ge-1,75\Rightarrow-1,75\le x\le1,75\\x\ge1,75;x\le-1,75\text{(Vô lý)}\end{cases}}\)
Vậy \(MinB=7\Leftrightarrow-1,75\le x\le1,75\)

Bài 6
a) (3x² + 5) + [(2x² - 5x) - (5x² + 4)]
= 3x² + 5 + (2x² - 5x - 5x² - 4)
= 3x² + 5 + 2x² - 5x - 5x² - 4
= (3x² + 2x² - 5x²) - 5x + (5 - 4)
= -5x + 1
---------‐----------
b) (x + 2)(x² - 2x + 4)
= x.x² - x.2x + x.4 + 2.x² - 2.2x + 2.4
= x³ - 2x² + 4x + 2x² - 4x + 8
= x³ + (-2x² + 2x²) + (4x - 4x) + 8
= x³ + 8
-------------------
c) (4x³ - 8x² + 13x - 5) : (2x - 1)
= (4x³ - 2x² - 6x² + 3x + 10x - 5) : (2x - 1)
= [(4x³ - 2x²) - (6x² - 3x) + (10x - 5)] : (2x - 1)
= [2x²(2x - 1) - 3x(2x - 1) + 5(2x - 1)] : (2x - 1)
= (2x - 1)(2x² - 3x + 5) : (2x - 1)
= 2x² - 3x + 5

Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=k$
$\Rightarrow a=bk, c=dk$. Khi đó:
$\frac{a-b}{b}=\frac{bk-b}{b}=\frac{b(k-1)}{b}=k-1(1)$
$\frac{c-d}{d}=\frac{dk-d}{d}=\frac{d(k-1)}{d}=k-1(2)$
Từ $(1); (2)\Rightarrow \frac{a-b}{b}=\frac{c-d}{d}$
-------------------
$\frac{2a+3b}{2a-3b}=\frac{2bk+3b}{2bk-3b}=\frac{b(2k+3)}{b(2k-3)}=\frac{2k+3}{2k-3}(3)$
$\frac{2c+3d}{2c-3d}=\frac{2dk+3d}{2dk-3d}=\frac{d(2k+3)}{d(2k-3)}=\frac{2k+3}{2k-3}(4)$
Từ $(3); (4)\Rightarrow \frac{2a+3b}{2a-3b}=\frac{2c+3d}{2c-3d}$

Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$

1: \(75^3:\left(-25\right)^3=\left(\dfrac{75}{-25}\right)^3=\left(-3\right)^3=-27\)
2: \(\left(-60\right)^2:\left(-5\right)^2=\dfrac{60^2}{5^2}=12^2=144\)
3: \(169^2:\left(-13\right)^2=\dfrac{169^2}{13^2}=\left(\dfrac{169}{13}\right)^2=13^2=169\)
4: \(\left(\dfrac{1}{2}\right)^2:\left(\dfrac{3}{2}\right)^2=\left(\dfrac{1}{2}:\dfrac{3}{2}\right)^2=\left(\dfrac{1}{3}\right)^2=\dfrac{1}{9}\)
5: \(\left(\dfrac{2}{3}\right)^3:\left(\dfrac{8}{27}\right)^3=\left(\dfrac{2}{3}:\dfrac{8}{27}\right)^3=\left(\dfrac{2}{3}\cdot\dfrac{27}{8}\right)^3=\left(\dfrac{9}{4}\right)^3=\dfrac{729}{64}\)
6: \(\left(\dfrac{5}{4}\right)^4:\left(\dfrac{15}{2}\right)^4=\left(\dfrac{5}{4}:\dfrac{15}{2}\right)^4=\left(\dfrac{5}{4}\cdot\dfrac{2}{15}\right)^4=\left(\dfrac{1}{6}\right)^4=\dfrac{1}{1296}\)
7: \(\left(\dfrac{7}{8}\right)^5:\left(\dfrac{21}{16}\right)^5\)
\(=\left(\dfrac{7}{8}:\dfrac{21}{16}\right)^5\)
\(=\left(\dfrac{7}{8}\cdot\dfrac{16}{21}\right)^5=\left(\dfrac{2}{3}\right)^5=\dfrac{32}{243}\)
8: \(\left(\dfrac{5}{6}\right)^4:\left(\dfrac{25}{18}\right)^4=\left(\dfrac{5}{6}:\dfrac{25}{18}\right)^4=\left(\dfrac{5}{6}\cdot\dfrac{18}{25}\right)^4=\left(\dfrac{3}{5}\right)^4=\dfrac{81}{625}\)
9:
\(\left(-\dfrac{3}{4}\right)^3:\left(\dfrac{9}{8}\right)^3=\left(-\dfrac{3}{4}:\dfrac{9}{8}\right)^3=\left(-\dfrac{3}{4}\cdot\dfrac{8}{9}\right)^3\)
\(=\left(-\dfrac{2}{3}\right)^3=-\dfrac{8}{27}\)
10:
\(\left(\dfrac{9}{10}\right)^6:\left(\dfrac{27}{-20}\right)^6=\left(\dfrac{9}{10}:\dfrac{-27}{20}\right)^6\)
\(=\left(\dfrac{9}{10}\cdot\dfrac{20}{-27}\right)^6=\left(-\dfrac{2}{3}\right)^6=\dfrac{64}{729}\)

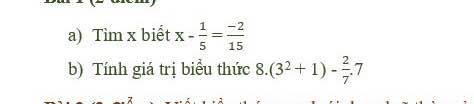





 giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
a) \(x-\dfrac{1}{5}=\dfrac{-2}{15}\)
\(\Rightarrow x=\dfrac{-2}{15}+\dfrac{1}{5}\)
\(\Rightarrow x=\dfrac{-2}{15}+\dfrac{3}{15}\)
\(\Rightarrow x=\dfrac{1}{15}\)
b) \(8\cdot\left(3^2+1\right)-\dfrac{2}{7}\cdot7\)
\(=8\cdot\left(9+1\right)-\dfrac{2\cdot7}{7}\)
\(=8\cdot10-2\)
\(=80-2\)
\(=78\)