K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DH
1
23 tháng 9 2021
Xét tam giác ABH vuông tại H có:
\(sinB=\dfrac{AH}{AB}=0,5\Rightarrow AB=\dfrac{AH}{0,5}=\dfrac{5}{0,5}=10\)
Xét tam giác ABH vuông tại H có:
\(AB^2=AH^2+BH^2\left(Pytago\right)\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{10^2-5^2}=5\sqrt{3}\)
19 tháng 8 2021
Bài 2:
Áp dụng định lí Pytago vào ΔEFG vuông tại E, ta được:
\(FG^2=EF^2+EG^2\)
\(\Leftrightarrow FG^2=15^2+5^2=250\)
hay \(FG=5\sqrt{10}\left(cm\right)\)
DH
0
MD
1
25 tháng 1
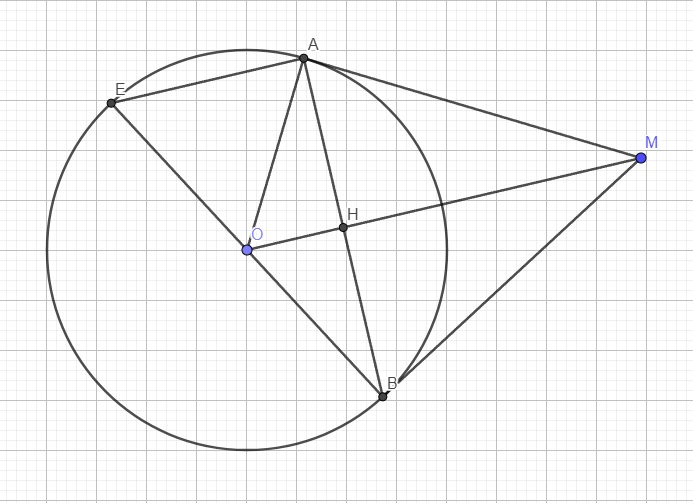
1: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>BD\(\perp\)AC tại D
Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại F
2: Xét ΔFBH vuông tại F và ΔFAC vuông tại F có
\(\widehat{FBH}=\widehat{FAC}\left(=90^0-\widehat{ACF}\right)\)
Do đó: ΔFBH~ΔFAC
=>\(\dfrac{FB}{FA}=\dfrac{FH}{FC}\)
=>\(FB\cdot FC=FA\cdot FH\)
3: Xét tứ giác AEHD có
\(\widehat{AEH}+\widehat{ADH}=90^0+90^0=180^0\)
nên AEHD là tứ giác nội tiếp đường tròn đường kính AH
Tâm I là trung điểm của AH
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 1
a.
Do MA là tiếp tuyến tại A \(\Rightarrow MA\perp OA\Rightarrow\widehat{MAO}=90^0\)
Xét hai tam giác OMA và OMB có:
\(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\\OM\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OMA=\Delta OMB\left(c.c.c\right)\)
\(\Rightarrow\widehat{MBO}=\widehat{MAO}=90^0\)
\(\Rightarrow MB\perp OB\Rightarrow MB\) là tiếp tuyến
b.
Gọi H là giao điểm AB và OM
Ta có: \(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow OM\) là trung trực AB
\(\Rightarrow OM\perp AB\) tại H đồng thời \(HA=HB=\dfrac{AB}{2}\)
Trong tam giác vuông OMA: \(cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{2}{2R}=\dfrac{1}{2}\Rightarrow\widehat{AOM}=60^0\)
\(\Rightarrow\widehat{AMO}=90^0-\widehat{AOM}=30^0\)
\(\Rightarrow\widehat{AMB}=2\widehat{AMO}=60^0\)
\(\Rightarrow\Delta AMB\) đều (tam giác cân có 1 góc bằng 60 độ)
Trong tam giác vuông OAH:
\(AH=OA.sin\widehat{AOM}=R.sin60^0=\dfrac{R\sqrt{3}}{3}\)
\(\Rightarrow AB=2AH=R\sqrt{3}\)
\(OH=OA.cos\widehat{AOM}=R.cos30^0=\dfrac{R}{2}\)
\(\Rightarrow HM=OM-OH=\dfrac{3R}{2}\)
\(\Rightarrow S_{ABM}=\dfrac{1}{2}HM.AB=\dfrac{3R^2\sqrt{3}}{4}\)
c.
BE là đường kính \(\Rightarrow\widehat{BAE}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{BAE}=90^0\Rightarrow AB\perp AE\)
Mà \(AB\perp OM\) (theo cm câu b)
\(\Rightarrow AE||OM\) (cùng vuông góc AB)
13 tháng 3 2023
15:
a: \(\text{Δ}=\left(m^2-m+2\right)^2-4m^2\)
=(m^2-m+2-2m)(m^2-m+2+2m)
=(m^2+m+2)(m^2-3m+2)
=(m-1)(m-2)(m^2+m+2)
Để phương trình co hai nghiệm phân biệt thì (m-1)(m-2)(m^2+m+2)>0
=>(m-1)(m-2)>0
=>m>2 hoặc m<1
b: x1+x2=m^2-m+2>0 với mọi m
x1*x2=m^2>0 vơi mọi m
=>Phương trình luôn có hai nghiệm dương phân biệt
ML
0
1 tháng 3 2022
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2+x-2=0\\y=x^2\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}\left(x+2\right)\left(x-1\right)=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(-2;4\right);\left(1;1\right)\right\}\)
30 tháng 9 2021
\(a,\Leftrightarrow\left(2x-2-\sqrt{3}\right)\left(2x+2+\sqrt{3}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x=2+\sqrt{3}\\2x=-2-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2+\sqrt{3}}{2}\\x=\dfrac{-2-\sqrt{3}}{2}\end{matrix}\right.\\ b,ĐK:x\ge0\\ PT\Leftrightarrow\left(\sqrt{x}-\sqrt{13}\right)^2-\left(2\sqrt{13}\right)^2=0\\ \Leftrightarrow\left(\sqrt{x}-3\sqrt{13}\right)\left(\sqrt{x}+\sqrt{13}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=3\sqrt{13}\\\sqrt{x}=-\sqrt{13}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=117\left(tm\right)\\x\in\varnothing\left(\sqrt{x}\ge0\right)\end{matrix}\right.\\ \Leftrightarrow x=117\)
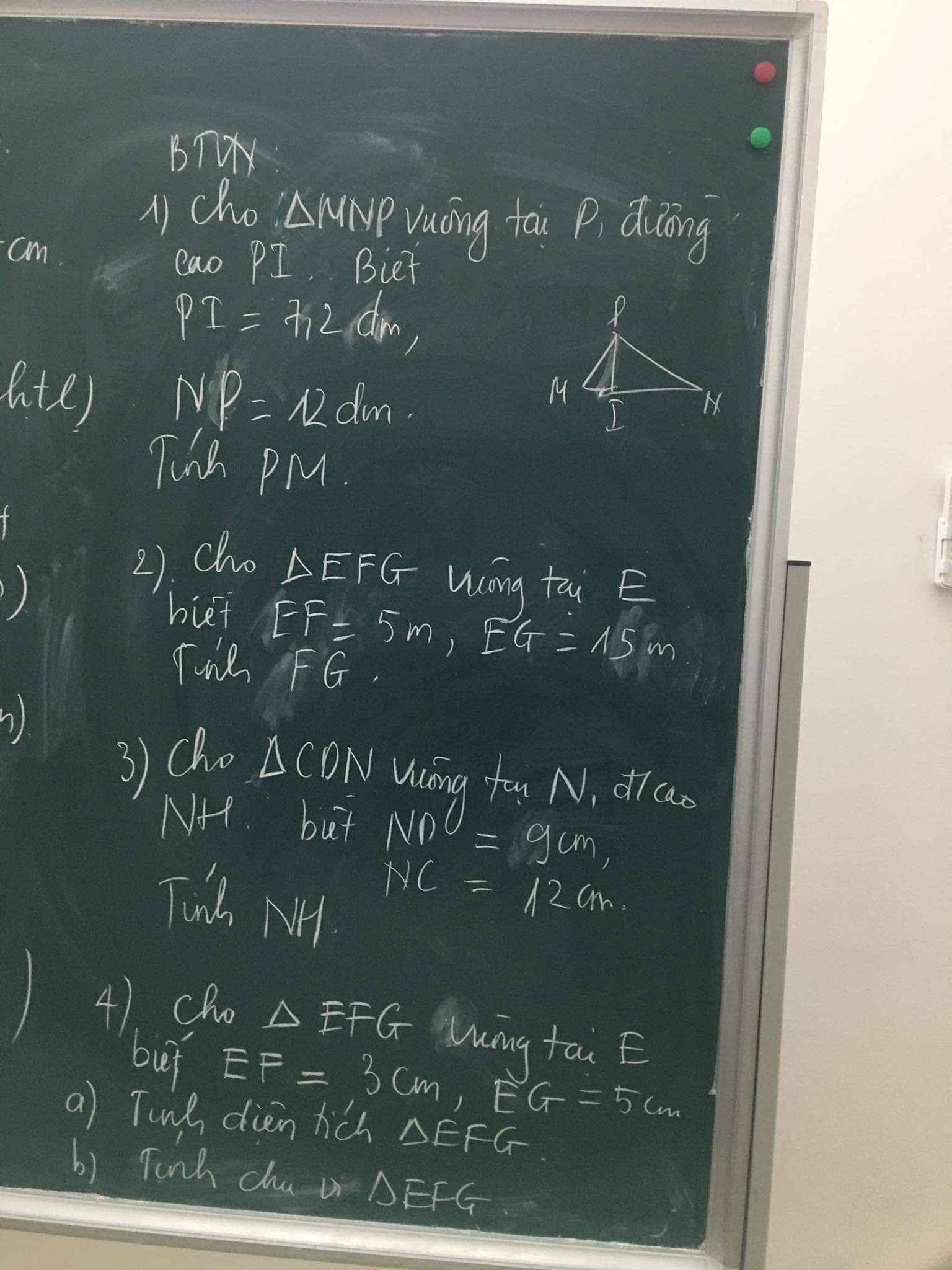
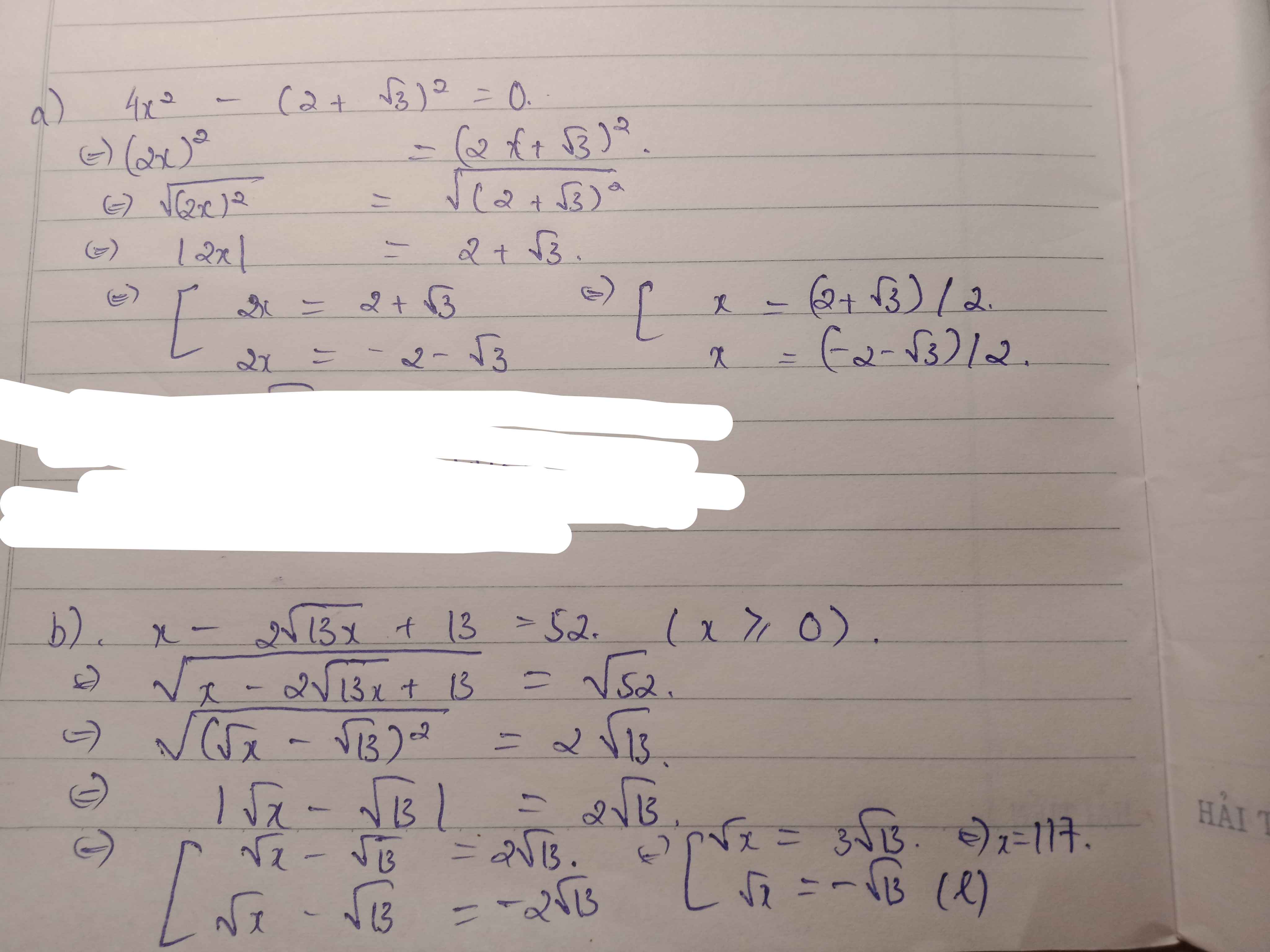
AC =\(4\sqrt{2}\left(cm\right)\)(theo Pytago)
\(\sin B=\frac{AC}{BC}=\frac{4}{4\sqrt{2}}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\)
\(\cos B=\frac{AB}{BC}=\frac{4}{4\sqrt{2}}=\frac{\sqrt{2}}{2}\)
\(\tan B=\frac{AC}{AB}=\frac{4}{4}=1\)
\(\cot B=\frac{AC}{AB}=\frac{4}{4}=1\)