Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình chịu bạn ạ
k mình nha
Chúc bạn học giỏi
Mình cảm ơn bạn nhiều
Cái này bạn phải đến lớp 8 để sử dụng đường trung bình mới giải đc :)
-Giải =cách đừng trung bình dễ lắm bạn ạ

Các trường hợp bằng nhau của tam giác thường là:
+) cạnh.cạnh.cạnh (c.c.c)
+) cạnh.góc.cạnh (c.g.c)
+) Góc.cạnh.góc (g.c.g)
Các trường hợp bằng nhau trong tam giác vuông là:
+) Hai cạnh góc vuông
+) Cạnh góc vuông và một góc nhọn kề cạnh ấy
+) Cạnh huyền và một góc nhọn kề cạnh ấy
+) Cạnh huyền và một cạnh góc vuông
Mik trả lời có đúng ko ạ nếu đúng bạn k nha
Các trường hợp bằng nhau của tam giác thường là:
+) cạnh.cạnh.cạnh (c.c.c)
+) cạnh.góc.cạnh (c.g.c)
+) Góc.cạnh.góc (g.c.g)
Các trường hợp bằng nhau trong tam giác vuông là:
+) Hai cạnh góc vuông
+) Cạnh góc vuông và một góc nhọn kề cạnh ấy
+) Cạnh huyền và một góc nhọn kề cạnh ấy
+) Cạnh huyền và một cạnh góc vuông

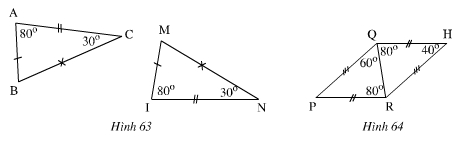
Hình 63
Ta có:
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
Hình 64 :
ΔPQR có:
Và QH = RP, HR = PQ, QR ( cạnh chung )
Nên ΔHQR = ΔPRQ

Các trường hợp bằng nhau của tam giác vuông:
-Hai cạnh góc vuông
-Cạnh góc vuông-góc nhọn kề
-Cạnh huyền-góc nhọn
-Cạnh huyền-cạnh góc vuông

a/ \(\Delta ADE\)vuông và \(\Delta ADF\)vuông có:
\(\widehat{EAD}=\widehat{DAF}\)(AD là đường phân giác của \(\Delta ABC\))
Cạnh huyền AD chung
=> \(\Delta ADE\)vuông = \(\Delta ADF\)vuông (cạnh huyền - góc nhọn)
=> DE = DF (hai cạnh tương ứng) (đpcm)
b/ \(\Delta ABD\)và \(\Delta ACD\)có:
AB = AC (\(\Delta ABC\)cân tại A)
\(\widehat{EAD}=\widehat{DAF}\)(AD là đường phân giác của \(\Delta ABC\))
Cạnh AD chung
=> \(\Delta ABD\)= \(\Delta ACD\)(c. g. c)
Ta có AB = AC (\(\Delta ABC\)cân tại A)
=> A thuộc đường trung trực của BC
=> AD \(\perp\)BC (đpcm)
c/ Ta có AD là đường phân giác của \(\Delta ABC\)
=> \(\widehat{DAB}=\frac{\widehat{BAC}}{2}=\frac{80^o}{2}=40^o\)(tính chất tia phân giác)
và \(\widehat{EDA}=90^o-\widehat{DAB}\)(\(\Delta ADB\)vuông tại D)
=> \(\widehat{EDA}=90^o-40^o=50^o\)
Ta lại có: \(\widehat{DAB}< \widehat{EDA}\)(vì 40o < 50o)
=> DE < AE (quan hệ giữa góc và cạnh đối diện trong tam giác)
và \(\hept{\begin{cases}DA< AE\\DA< DE\end{cases}}\)(quan hệ giữa đường vuông góc và đường xiên)
=> DA < DE < AE (đpcm)
a)Xét tam giác EAD và FAD có
AÊD= góc AFD=90*
AD là cạnh chung
góc EAD=góc FAD(tam giác ABC cân)
=>tam giác ...=...(cạnh huyền-góc nhọn)
=>DE=DF
b)Xét tam giác ABD và ACD có
BA=CA(gt)
BÂD=CÂD(gt)
AD là cạnh chung
=>tam giác ...=...(c-g-c)
=>góc BDA=CDA
mà BDA+CDA=180*
=>BDA=CDA=180*/2=90*
=>AD vuông góc với BC
c) Xét tam giác AED có: AÊD+EÂD+ góc EDA=180*
=>90*+(80*/2)+góc EAD=180*
=>90*+40*+góc EAD=180*
=>góc EAD=180*-(90*+40*)
=>góc EAD=50*
ta có:EÂD<góc ADE<AÊD(40*<50*<90*)
=>ED<AE<AD
Vậy, ED<AE<AD.
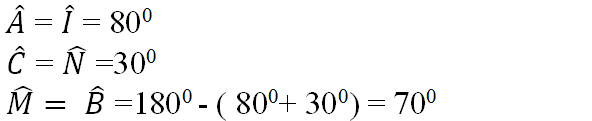
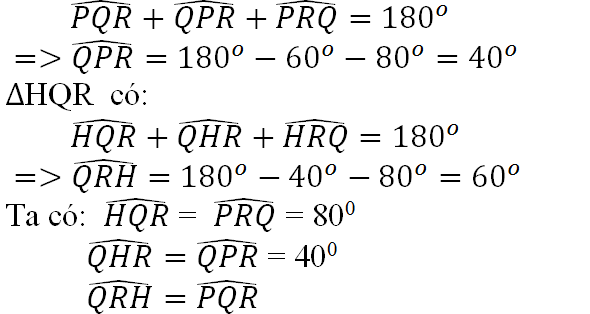
a) ∆OAD và ∆OCB có: OA= OC(gt)
∠O chung
OB = OD (gt)
OAD = OCB (c.g.c) AD = BC
Nên ∆OAD=∆OCB(c.g.c)
suy ra AD=BC.
b)
Ta có ∠A1 = 1800 – ∠A2
∠C1 = 1800 – ∠C2
mµ ∠A2 = ∠C2 do ΔOAD = ΔOCB (c/m trên)
⇒ ∠A1 = ∠C1
Ta có OB = OA + AB
OD = OC + CD mà OB = OD, OA = OC ⇒ AB = CD
Xét ΔEAB = ΔECD có:
∠A1 = ∠C1 (c/m trên)
AB = CD (c/m trên)
∠B1 = ∠D1 (ΔOCB = ΔOAD)
⇒ ΔEAB = ΔECD (g.c.g)
c) Xét ΔOBE và ΔODE có:
OB = OD (GT)
OE chung
AE = CE (ΔAEB = ΔCED) ⇒ΔOBE = ΔODE (c.c.c)
⇒ ∠AOE = ∠COE ⇒ OE là phân giác của góc ∠xOy.