K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
1
18 tháng 9 2023
Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:
\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
10 tháng 9
Kết luận của định lý ứng với hình vẽ là:
\(\hat{tOz}\) = 90\(^0\)
11 tháng 9
Bài 2:
a: \(A=\frac17+\frac{1}{7^2}+\cdots+\frac{1}{7^{100}}\)
=>\(7A=1+\frac17+\cdots+\frac{1}{7^{99}}\)
=>\(7A-A=1+\frac17+\cdots+\frac{1}{7^{99}}-\frac17-\frac{1}{7^2}-\cdots-\frac{1}{7^{100}}\)
=>\(6A=1-\frac{1}{7^{100}}=\frac{7^{100}-1}{7^{100}}\)
=>\(A=\frac{7^{100}-1}{6\cdot7^{100}}\)
b: \(B=\frac53+\frac{5}{3^2}+\frac{5}{3^3}+\cdots+\frac{5}{3^{20}}\)
=>\(3B=5+\frac53+\frac{5}{3^2}+\cdots+\frac{5}{3^{19}}\)
=>\(3B-B=5+\frac53+\frac{5}{3^2}+\cdots+\frac{5}{3^{19}}-\frac53-\frac{5}{3^2}-\cdots-\frac{5}{3^{20}}\)
=>\(2B=5-\frac{5}{3^{20}}=\frac{5\cdot3^{20}-5}{3^{20}}\)
=>\(B=\frac{5\cdot3^{20}-5}{2\cdot3^{20}}\)
c: \(C=-\frac13+\frac{1}{3^2}-\frac{1}{3^3}+\frac{1}{3^4}-\cdots+\frac{1}{3^{50}}\)
=>\(3C=-1+\frac13-\frac{1}{3^2}+\frac{1}{3^3}-\cdots+\frac{1}{3^{49}}\)
=>\(3C+C=-1+\frac13-\frac{1}{3^2}+\frac{1}{3^3}-\cdots+\frac{1}{3^{49}}-\frac13+\frac{1}{3^2}-\frac{1}{3^3}+\frac{1}{3^4}-\cdots+\frac{1}{3^{50}}\)
=>\(4C=-1+\frac{1}{3^{50}}=\frac{-3^{50}+1}{3^{50}}\)
=>\(C=\frac{-3^{50}+1}{4\cdot3^{50}}\)
d: \(D=\left(-\frac17\right)^0+\left(-\frac17\right)^1+\left(-\frac17\right)^2+\cdots+\left(-\frac17\right)^{2017}\)
=>\(D=1-\frac17+\frac{1}{7^2}-\frac{1}{7^3}+\cdots-\frac{1}{7^{2017}}\)
=>\(7D=7-1+\frac17-\frac{1}{7^2}+\cdots-\frac{1}{7^{2016}}\)
=>\(7D+D=7-1+\frac17-\frac{1}{7^2}+\cdots-\frac{1}{7^{2016}}+1-\frac17+\frac{1}{7^2}-\frac{1}{7^3}+\cdots-\frac{1}{7^{2017}}\)
=>\(8D=7-\frac{1}{7^{2017}}=\frac{7^{2018}-1}{7^{2017}}\)
=>\(D=\frac{7^{2018}-1}{8\cdot7^{2017}}\)
e: \(E=\frac12+\frac{1}{2^3}+\frac{1}{2^5}+\cdots+\frac{1}{2^{99}}\)
=>\(4E=2+\frac12+\frac{1}{2^3}+\cdots+\frac{1}{2^{97}}\)
=>\(4E-E=2+\frac12+\frac{1}{2^3}+\cdots+\frac{1}{2^{97}}-\frac12-\frac{1}{2^3}-\frac{1}{2^5}-\cdots-\frac{1}{2^{99}}\)
=>\(3E=2-\frac{1}{2^{99}}=\frac{2^{100}-1}{2^{99}}\)
=>\(E=\frac{2^{100}-1}{3\cdot2^{99}}\)
Bài 1:
a: \(A=2\cdot4+4\cdot6+6\cdot8+\cdots+98\cdot100\)
\(=4\left(1\cdot2+2\cdot3+3\cdot4+\cdots+49\cdot50\right)\)
\(=4\left\lbrack1\left(1+1\right)+2\left(2+1\right)+3\left(3+1\right)+\cdots+49\left(49+1\right)\right\rbrack\)
\(=4\left\lbrack\left(1^2+2^2+\cdots+49^2\right)+\left(1+2+3+\cdots+49\right)\right\rbrack\)
\(=4\cdot\left\lbrack\frac{49\left(49+1\right)\left(2\cdot49+1\right)}{6}+\frac{49\cdot50}{2}\right\rbrack=4\cdot\left\lbrack\frac{49\cdot50\cdot99}{6}+49\cdot25\right\rbrack\)
\(=4\cdot\left\lbrack49\cdot25\cdot33+49\cdot25\right\rbrack=4\cdot49\cdot25\cdot34=100\cdot49\cdot34\)
=166600
b: \(B=1\cdot99+2\cdot98+\cdots+97\cdot3+98\cdot2+99\cdot1\)
\(=2\cdot\left(1\cdot99+2\cdot98+\cdots+48\cdot52+49\cdot51\right)+50^2\)
\(=2\cdot\left\lbrack1\left(100-1\right)+2\left(100-2\right)+\cdots+48\left(100-48\right)+49\left(100-49\right)\right\rbrack+50^2\)
\(=2\left\lbrack100\left(1+2+\cdots+49\right)-\left(1^2+2^2+\cdots+49^2\right)\right\rbrack\) +2500
\(=2\cdot\left\lbrack100\cdot\frac{49\cdot50}{2}-\frac{49\cdot\left(49+1\right)\left(2\cdot49+1\right)}{6}\right\rbrack+2500\)
\(=2\cdot\left\lbrack100\cdot49\cdot25-\frac{49\cdot50\cdot99}{6}\right\rbrack+2500\)
\(=2\cdot\left\lbrack100\cdot49\cdot25-49\cdot25\cdot33\right\rbrack+2500=2\cdot25\cdot49\left(100-33\right)+2500\)
\(=50\cdot49\cdot67+2500=166650\)
d: \(D=2^2+4^2+\cdots+98^2+100^2\)
\(=2^2\left(1^2+2^2+\cdots+49^2+50^2\right)\)
\(=4\cdot\frac{50\cdot\left(50+1\right)\left(2\cdot50+1\right)}{6}=4\cdot\frac{50\cdot51\cdot101}{6}\)
\(=4\cdot25\cdot17\cdot101=100\cdot17\cdot101=171700\)
e: \(E=1^2+3^2+5^2+\cdots+99^2\)
\(=\left(1^2+2^2+3^2+4^2+\cdots+99^2+100^2\right)-\left(2^2+4^2+\cdots+100^2\right)\)
\(=\frac{100\left(100+1\right)\left(2\cdot100+1\right)}{6}-2^2\left(1^2+2^2+\cdots+50^2\right)\)
\(=\frac{100\cdot101\cdot201}{6}-4\cdot\frac{50\left(50+1\right)\left(2\cdot50+1\right)}{6}\)
\(=50\cdot101\cdot67-4\cdot\frac{50\cdot51\cdot101}{6}\)
\(=50\cdot101\cdot67-4\cdot25\cdot17\cdot101=101\cdot50\left(67-2\cdot17\right)\)
\(=50\cdot101\cdot33=166650\)
f: \(F=1^2-2^2+3^2-4^2+\cdots+99^2-100^2\)
\(=\left(1-2\right)\left(1+2\right)+\left(3-4\right)\left(3+4\right)+\cdots+\left(99-100\right)\left(99+100\right)\)
=-(1+2+3+4+...+99+100)
\(=-100\cdot\frac{101}{2}=-50\cdot101=-5050\)
QT
1
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
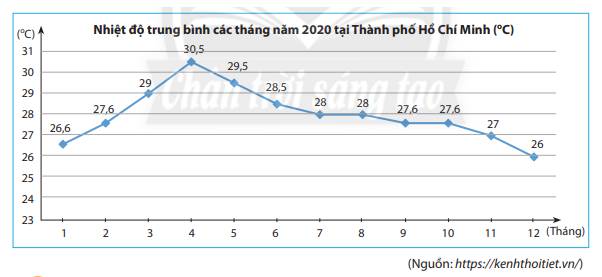
+ Biểu đồ biểu diễn nhiệt độ trung bình các tháng năm 2020 tại Thành phố Hồ Chí Minh.
+ Đơn vị thời gian là tháng, đơn vị số liệu là độ C.
+ Tháng 4 có nhiệt độ trung bình cao nhất.
+ Tháng 12 có nhiệt độ trung bình thấp nhất.
+ Nhiệt độ trung bình tăng trong những khoảng thời gian từ tháng: 1 – 2; 2 – 3; 3 – 4.
+ Nhiệt độ trung bình giảm trong những khoảng thời gian từ tháng: 4 – 5; 5 – 6; 6 – 7; 8 – 9; 10 – 11; 11 – 12.
+ Nhiệt độ trung bình không đổi trong những khoảng thời gian từ tháng: 7 – 8; 9 – 10.
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
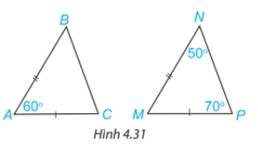
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
QT
1
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat M + {50^o} + {70^o} = {180^o}\\ \Rightarrow \widehat M = {60^o}\end{array}\)
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP} (=60^0)\)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
2 góc kề bù trong hình là: góc mOt và tOn
Ta có:
\(\begin{array}{l}\widehat {mOt} + \widehat {tOn} = 180^\circ \\\widehat {mOt} = 180^\circ - \widehat {tOn} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
gải thích hộ với ạ
2:
ΔABC,ΔABD đều có 3 cạnh bằng nhau
=>AB=BC=AC và AB=BD=AD
=>AB=BC=AC=DB=AD
Xét ΔACD và ΔBCD có
AC=BC
CD chung
AD=BD
=>ΔACD=ΔBCD
=>góc ACD=góc BCD
=>CD là phân giác của góc ACB
1:
a: Xét ΔABD và ΔCDB có
AB=CD
BD chung
AD=BC
=>ΔABD=ΔCDB
b: ΔABD=ΔCDB
=>góc ADB=góc CBD