
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi O là tâm đường tròn \(\Rightarrow\) O là trung điểm BC
\(\stackrel\frown{BE}=\stackrel\frown{ED}=\stackrel\frown{DC}\Rightarrow\widehat{BOE}=\widehat{EOD}=\widehat{DOC}=\dfrac{180^0}{3}=60^0\)
Mà \(OD=OE=R\Rightarrow\Delta ODE\) đều
\(\Rightarrow ED=R\)
\(BN=NM=MC=\dfrac{2R}{3}\Rightarrow\dfrac{NM}{ED}=\dfrac{2}{3}\)
\(\stackrel\frown{BE}=\stackrel\frown{DC}\Rightarrow ED||BC\)
Áp dụng định lý talet:
\(\dfrac{AN}{AE}=\dfrac{MN}{ED}=\dfrac{2}{3}\Rightarrow\dfrac{EN}{AN}=\dfrac{1}{2}\)
\(\dfrac{ON}{BN}=\dfrac{OB-BN}{BN}=\dfrac{R-\dfrac{2R}{3}}{\dfrac{2R}{3}}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{EN}{AN}=\dfrac{ON}{BN}=\dfrac{1}{2}\) và \(\widehat{ENO}=\widehat{ANB}\) (đối đỉnh)
\(\Rightarrow\Delta ENO\sim ANB\left(c.g.c\right)\)
\(\Rightarrow\widehat{NBA}=\widehat{NOE}=60^0\)
Hoàn toàn tương tự, ta có \(\Delta MDO\sim\Delta MAC\Rightarrow\widehat{MCA}=\widehat{MOD}=60^0\)
\(\Rightarrow\Delta ABC\) đều


Đề 1: TỰ LUẬN
Câu 1: sin 60o31' = cos 29o29'
cos 75o12' = sin 14o48'
cot 80o = tan 10o
tan 57o30' = cot 32o30'
sin 69o21' = cos 20o39'
cot 72o25' = 17o35'
- Chiều về mình làm cho nha nha ![]() Giờ mình đi học rồi
Giờ mình đi học rồi ![]() Bạn có gấp lắm hông
Bạn có gấp lắm hông ![]()

Bài 1:
Kẻ \(OM\perp AB\), \(OM\)cắt \(CD\)tại \(N\).
Khi đó \(MN=8cm\).
TH1: \(AB,CD\)nằm cùng phía đối với \(O\).
\(R^2=OC^2=ON^2+CN^2=h^2+\left(\frac{25}{2}\right)^2\)(\(h=CN\)) (1)
\(R^2=OA^2=OM^2+AM^2=\left(h+8\right)^2+\left(\frac{15}{2}\right)^2\)(2)
Từ (1) và (2) suy ra \(R=\frac{\sqrt{2581}}{4},h=\frac{9}{4}\).
TH2: \(AB,CD\)nằm khác phía với \(O\).
\(R^2=OC^2=ON^2+CN^2=h^2+\left(\frac{25}{2}\right)^2\)(\(h=CN\)) (3)
\(R^2=OA^2=OM^2+AM^2=\left(8-h\right)^2+\left(\frac{15}{2}\right)^2\)(4)
Từ (3) và (4) suy ra \(R=\frac{\sqrt{2581}}{4},h=\frac{-9}{4}\)(loại).
Bài 3:
Lấy \(A'\)đối xứng với \(A\)qua \(Ox\), khi đó \(A'\)có tọa độ là \(\left(1,-2\right)\).
\(MA+MB=MA'+MB\ge A'B\)
Dấu \(=\)xảy ra khi \(M\)là giao điểm của \(A'B\)với trục \(Ox\).
Suy ra \(M\left(\frac{5}{3},0\right)\).

Bài 3:
\(A=\sqrt{1-6x+9x^2}+\sqrt{9x^2-12x+4}\)
\(A=\sqrt{9x^2-3x-3x+1}+\sqrt{9x^2-6x-6x+4}\)
\(A=\sqrt{\left(3x-1\right)^2}+\sqrt{\left(3x-2\right)^2}\)
\(A=\left|3x-1\right|+\left|3x-2\right|\)
\(A=\left|3x-1\right|+\left|2-3x\right|\)
Áp dụng bất đẳng thức \(\left|A\right|+\left|B\right|\ge\left|A+B\right|\) ta có:
\(\left|3x-1\right|+\left|2-3x\right|\ge\left|3x-1+2-3x\right|\)
\(\Rightarrow\left|3x-1\right|+\left|2-3x\right|\ge\left|1\right|=1\)
Dấu "=" sảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}3x-1\ge0\\2-3x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3x\ge1\\3x\le2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{3}\\x\le\dfrac{2}{3}\end{matrix}\right.\)
\(\Rightarrow\dfrac{1}{3}\le x\le\dfrac{2}{3}\)
Vậy............
Chúc bạn học tốt!!!




Lời giải:
a) $MA,MB$ là tiếp tuyến của $(O)$ nên $MA\perp OA, MB\perp OB$
$\Rightarrow \widehat{MAO}=\widehat{MBO}=90^0$
Tứ giác $MAOB$ có tổng 2 góc đối $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$ nên là tứ giác nội tiếp.
b) Xét tam giác $MAC$ và $MDA$ có:
$\widehat{M}$ chung
$\widehat{MAC}=\widehat{MDA}$ (tính chất góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp chắn cung đó)
$\Rightarrow \triangle MAC\sim \triangle MDA$ (g.g)
$\Rightarrow \frac{MA}{MD}=\frac{MC}{MA}\Rightarrow MA^2=MC.MD$
c) Dễ thấy $AB\perp MO$ tại $H$.
Xét tam giác $AMO$ vuông tại $A$ có đường cao $AH$, áp dụng định lý hệ thức lượng trong tam giác vuông:
$MA^2=MH.MO$
Kết hợp kết quả phần b suy ra $MH.MO=MC.MD$
$\Rightarrow CHOD$ là tứ giác nội tiếp.
d) Vận dụng giả thiết $AD\parallel MB$ và tính chất góc tạo bởi tiếp tuyến- dây cung ta có:
$\widehat{MCB}=180^0-\widehat{CMB}-\widehat{CBM}$
$=180^0-\widehat{CDA}-\widehat{CDB}$
$=180^0-\widehat{ADB}=\widehat{ACB}$ (do $ACBD$ là tứ giác nội tiếp)
** Khuyên chân thành các bạn muốn nâng cao xác suất được hỗ trợ thì nên chịu khó gõ đề bằng công thức toán. Chụp hình như này đọc bài rất nản, đặc biệt là hình xoay ngược đọc mỏi cổ lém.
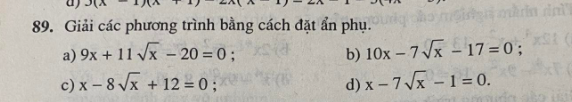




 Giải nhanh hộ mình nha all
Giải nhanh hộ mình nha all







c: \(\Leftrightarrow\left(\sqrt{x}-2\right)\cdot\left(\sqrt{x}-6\right)=0\)
=>x=4 hoặc x=36
d: Đặt \(\sqrt{x}=a\)
Pt sẽ là \(a^2-a-7=0\)
\(\text{Δ}=\left(-1\right)^2-4\cdot1\cdot\left(-7\right)=29>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}a_1=\dfrac{1-\sqrt{29}}{2}\left(loại\right)\\a_2=\dfrac{1+\sqrt{29}}{2}\left(nhận\right)\end{matrix}\right.\)
\(\Leftrightarrow\sqrt{x}=\dfrac{\sqrt{29}+1}{2}\)
hay \(x=\dfrac{30+2\sqrt{29}}{4}=\dfrac{15+\sqrt{29}}{2}\)
c) Đặt \(\sqrt{x}=a\left(a\ge0\right)\)
Ta có PT
\(a^2-8a+12=0\)
\(\Delta=\left(-8\right)^2-4.12=64-48=16>0\)
PT có 2 nghiệm phân biệt
\(\left[{}\begin{matrix}a_1=\dfrac{8+\sqrt{16}}{2}=\dfrac{12}{2}=6\\a_2=\dfrac{8-\sqrt{16}}{2}=\dfrac{4}{2}=2\end{matrix}\right.\)
Ta có
Với a = 6 thì \(\sqrt{x}=6\Leftrightarrow x=36\left(tm\right)\)
Với a = 2 thì \(\sqrt{x}=2\Leftrightarrow x=4\left(tm\right)\)