
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3. Xét tam giác ADM và tam giác AEM có :
góc ADM = góc AEM = 90 độ
Góc BAM = góc CAM (gt)
AM chung
=>Tam giác ADM = tam giác AEm (c.huyền - g.nhọn)
=>MD = ME (cặp cạnh t/ứng )
AD = AE (cặp cạnh t/ứng )
Xét tam giác MDB và tam giác MEC có :
MB = MC (gt)
góc MDB = góc MEC = 90 độ
MD = ME ( câu a)
=>Tam giác MDB = Tam giác MEC (c.huyền-c.g.vuông)
Vì AD + DB = AB
AE + EC = AC
Mà AD = AE
DB = EC
=>AB = AC
Xét tam giác ABM và tam giác ACM có
AM chung
góc BAM = góc CAM (gt)
AB = AC (CMT)
=>Tam giác ABM = Tam giác ACM (c.huyền-g.nhon)
Vậy có 3 cặp tam giác bằng nhau

Kẻ Cz//By (z thuộc nửa mặt phẳng bờ AC chứa B)
Ta có: góc zCB=góc CBy = 30 độ (so le trong)
Mà góc zCB + góc zCA=120 độ
=> góc zCA=90 độ.
=> Cz//Ax (cùng vuông góc AC)
Mà Cz//By => Ax//By


a: Xét ΔDBC vuông tại D và ΔECB vuông tại E có
BC chung
\(\widehat{DBC}=\widehat{ECB}\)
Do đo;ΔDBC=ΔECB
b: Xét ΔBHD vuông tại D và ΔCHE vuông tại E có
DB=CE
\(\widehat{DBH}=\widehat{ECH}\)
Do đó:ΔBHD=ΔCHE
c: Xét ΔHBC có \(\widehat{HBC}=\widehat{HCB}\)
nên ΔHBC cân tại H
=>HB=HC
mà AB=AC
nên AH là đường trung trực của BC


a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
BD=CE
\(\widehat{ABD}=\widehat{ACE}\)
Do đó: ΔABD=ΔACE
Suy ra: AB=AC
hay ΔABC cân tại A
b: XétΔABC có
AD là đường cao
CH là đường cao
AD cắt CH tại D
Do đó: D là trực tâm của ΔABC
=>BD vuông góc với AC

\(3^{x+1}+3^{x+3}=810\)
\(\Leftrightarrow3^{x+1}+3^{x+1}.3^2=810\)
\(\Leftrightarrow3^{x+1}.10=810\)
\(\Leftrightarrow3^{x+1}=81=3^4\)
\(\Leftrightarrow x+1=4\)
\(\Leftrightarrow x=3\)

Giải:
Do \(\left(2016a+13b-1\right)\left(2016^a+2016a+b\right)\) \(=2015\)
Nên \(2016a+13b-1\) và \(2016^a+2016a+b\) là 2 số lẻ \((*)\)
Ta xét 2 trường hợp:
Trường hợp 1: Nếu \(a\ne0\) thì \(2016^a+2016a\) là số chẵn
Do \(2016^a+2016a+b\) lẻ \(\Rightarrow b\) lẻ
Với \(b\) lẻ \(\Rightarrow13b-1\) chẵn do đó \(2016a+13b-1\) chẵn (trái với \((*)\))
Trường hợp 2: Nếu \(a=0\) thì:
\(\left(2016.0+13b-1\right)\left(2016^0+2016.0+b\right)\) \(=2015\)
\(\Leftrightarrow\left(13b-1\right)\left(b+1\right)=2015=1.5.13.31\)
Do \(b\in N\Rightarrow\left(13b-1\right)\left(b+1\right)=5.403=13.155\) \(=31.65\)
Và \(13b-1>b+1\)
\(*)\) Nếu \(b+1=5\Rightarrow b=4\Rightarrow13b-1=51\) (loại)
\(*)\) Nếu \(b+1=13\Rightarrow b=12\Rightarrow13b-1=155\) (chọn)
\(*)\) Nếu \(b+1=31\Rightarrow b=30\Rightarrow13b-1=389\) (loại)
Vậy \(\left(a,b\right)=\left(0;12\right)\)

\(\left|3x-5\right|+\left(2y+5\right)^{208}+\left(4z-3\right)^{20}\le0\)
\(\Leftrightarrow\hept{\begin{cases}3x-5=0\\2y+5=0\\4z-3=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{5}{3}\\y=-\frac{5}{2}\\z=\frac{3}{4}\end{cases}}\)
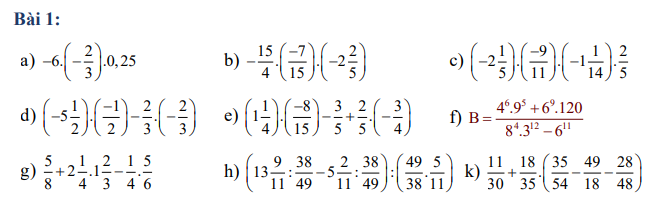

 M.n giải hộ em vs đg cần gấp ạ
M.n giải hộ em vs đg cần gấp ạ




 Giúp mk vs ạ mk cần gấp . Cmơn mn nhé 😘
Giúp mk vs ạ mk cần gấp . Cmơn mn nhé 😘



 mn giúp mk vs, mk cần gấp!!!cảm ơn trước ạ
mn giúp mk vs, mk cần gấp!!!cảm ơn trước ạ

a: \(-6\cdot\left(-\dfrac{2}{3}\right)\cdot0.25=6\cdot\dfrac{2}{3}\cdot\dfrac{1}{4}=4\cdot\dfrac{1}{4}=1\)
b: \(\dfrac{-15}{4}\cdot\dfrac{-7}{15}\cdot\left(-2\dfrac{2}{5}\right)\)
\(=\dfrac{7}{4}\cdot\dfrac{12}{5}\)
\(=\dfrac{84}{20}=\dfrac{21}{5}\)
c: \(\left(-2\dfrac{1}{5}\right)\cdot\left(-\dfrac{9}{11}\right)\cdot\left(-\dfrac{1}{14}\right)\cdot\dfrac{2}{5}\)
\(=-\dfrac{11}{5}\cdot\dfrac{2}{5}\cdot\dfrac{9}{11}\cdot\dfrac{1}{14}\)
\(=-\dfrac{11}{11}\cdot\dfrac{2}{14}\cdot\dfrac{9}{25}\)
\(=-\dfrac{9}{175}\)
\(a,=4\cdot0,25=1\\ b,=\dfrac{7}{4}\cdot\left(-\dfrac{12}{5}\right)=-\dfrac{21}{5}\\ c,=\left(-\dfrac{11}{5}\right)\left(-\dfrac{9}{11}\right)\left(-\dfrac{15}{14}\right)\cdot\dfrac{2}{5}\\ =\dfrac{9}{5}\cdot\left(-\dfrac{15}{14}\right)\cdot\dfrac{2}{5}=-\dfrac{27}{14}\cdot\dfrac{2}{5}=-\dfrac{27}{35}\\ d,=\left(-\dfrac{11}{2}\right)\left(-\dfrac{1}{2}\right)+\dfrac{4}{9}=\dfrac{11}{4}+\dfrac{4}{9}=\dfrac{115}{36}\\ e,=\dfrac{5}{4}\cdot\left(-\dfrac{8}{15}\right)-\dfrac{3}{5}-\dfrac{3}{10}=-\dfrac{2}{3}-\dfrac{3}{5}-\dfrac{3}{10}=-\dfrac{47}{30}\)
\(f,B=\dfrac{2^{12}\cdot3^{10}+2^9\cdot3^9\cdot2^3\cdot3\cdot5}{2^{12}\cdot3^{12}-2^{11}\cdot3^{11}}=\dfrac{2^{12}\cdot3^{10}\left(1+5\right)}{2^{11}\cdot3^{11}\left(6-1\right)}=\dfrac{2\cdot6}{5\cdot3}=\dfrac{4}{5}\\ g,=\dfrac{5}{8}+\dfrac{9}{4}\cdot\dfrac{5}{3}-\dfrac{5}{24}=\dfrac{5}{8}+\dfrac{15}{4}-\dfrac{5}{24}=\dfrac{25}{6}\\ h,=\dfrac{49}{38}\cdot\left(\dfrac{152}{11}-\dfrac{57}{11}\right):\dfrac{245}{418}=\dfrac{49}{38}\cdot\dfrac{418}{245}\cdot\dfrac{95}{11}=\dfrac{95\cdot11}{5\cdot11}=19\\ k,=\dfrac{11}{30}+\dfrac{18}{35}\cdot\dfrac{35}{54}-\dfrac{18}{35}\cdot\dfrac{49}{18}-\dfrac{18}{35}\cdot\dfrac{28}{48}\\ =\dfrac{11}{30}+\dfrac{1}{3}-\dfrac{7}{5}-\dfrac{3}{10}=-1\)