Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c)
\(\left\{\begin{matrix} -x^2+4x-7< 0\\ x^2-2x-1\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x^2-4x+7>0\\ x^2-2x+1\geq 2\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} (x-2)^2+3>0\\ (x-1)^2-2\geq 0\end{matrix}\right.\Leftrightarrow (x-1)^2-2\geq 0\Leftrightarrow \left[\begin{matrix} x-1\geq \sqrt{2}\\ x-1\leq -\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow \left[\begin{matrix} x\geq \sqrt{2}+1\\ x\leq 1-\sqrt{2}\end{matrix}\right.\)
d)
\(\left\{\begin{matrix} -2x^2-5x+4< 0\\ -x^2-3x+10>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2x^2+5x-4>0\\ (2-x)(x+5)>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2(x+\frac{5}{4})^2-\frac{57}{8}>0\\ (2-x)(x+5)>0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} (x+\frac{5}{4}-\frac{\sqrt{57}}{4})(x+\frac{5}{4}+\frac{\sqrt{57}}{4})>0\\ (2-x)(x+5)>0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \left[\begin{matrix} x>\frac{-5+\sqrt{57}}{4}\\ x< \frac{-5-\sqrt{57}}{4}\end{matrix}\right.\\ -5< x< 2\end{matrix}\right.\) \(\Rightarrow \left[\begin{matrix} -5< x< \frac{-5-\sqrt{57}}{4}\\ \frac{\sqrt{57}-5}{4}< x< 2\end{matrix}\right.\)
a)
\(\left\{\begin{matrix} 2x^2+9x+7>0\\ x^2+x-6< 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (x+1)(2x+7)>0\\ (x-2)(x+3)< 0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \left[\begin{matrix} x>-1\\ x< \frac{-7}{2}\end{matrix}\right.\\ -3< x< 2\end{matrix}\right.\Rightarrow -1< x< 2\)
b) \(\left\{\begin{matrix} 2x^2+x-6>0\\ 3x^2-10x+3\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (2x-3)(x+2)>0\\ (x-3)(3x-1)\geq 0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \left[\begin{matrix} x>\frac{3}{2}\\ x< -2\end{matrix}\right.\\ \left[\begin{matrix} x\geq 3\\ x\leq \frac{1}{3}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow \left[\begin{matrix} x\geq 3\\ x< -2\end{matrix}\right.\)

a)
\(\left\{{}\begin{matrix}x^2+x+5< 0\\x^2-6x+1>0\end{matrix}\right.\)
\(\)Ta có
\(x^2+x+5=\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{19}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}\ge\dfrac{19}{4}>0\)
=> Bất phương trình đàu tiên sai, hệ bất phương trình sai
b)
\(\left\{{}\begin{matrix}2x^2+x-6>0\\3x^2-10x+3\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(2x-3\right)\left(x+2\right)>0\\\left(x-3\right)\left(3x-1\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x>2\\x< -3\end{matrix}\right.\\\left[{}\begin{matrix}x\le-\dfrac{1}{3}\\x\ge3\end{matrix}\right.\end{matrix}\right.\)

Bai1:
\(-2x+\frac{3}{5}\le\frac{3\left(2x-7\right)}{3}\Leftrightarrow-10x+3\le5\left(2x-7\right)\Leftrightarrow-10x+3\le10x-35\)
\(\Leftrightarrow\left(10+10\right)x\ge3+35\Rightarrow x\ge\frac{38}{20}=\frac{19}{10}\)
Bài
\(\left\{\begin{matrix}x+m-1>0\\3m-2-x>0\end{matrix}\right.\Leftrightarrow\left(I\right)\left\{\begin{matrix}x>1-m\\x< 3m-2\end{matrix}\right.\)
Hệ (I) có nghiệm cần m thỏa mãn:
\(1-m< 3m-2\Leftrightarrow1+2< 3m+m\Rightarrow m>\frac{3}{2}\)
Kết luận: để hệ có nghiệm cần: m>3/2

\(\left(4x-5\right)\left(-x^2-3x+4\right)>=0\)
\(\Leftrightarrow\left(4x-5\right)\left(x^2+3x-4\right)< =0\)
=>(4x-5)(x+4)(x-1)<=0
BXD:

Theo BXD, ta được: x<=-4 hoặc 1<=x<=5/4
\(3x^2-7x+2>0\)
=>3x2-6x-x+2>0
=>(x-2)(3x-1)>0
=>x>2 hoặc x<1/3
=>x<=-4

a)
\(\left\{{}\begin{matrix}\left(2m-1\right)^2-4\left(m^2-m\right)\ge0\left(1\right)\\\dfrac{1}{m^2-m}>0\left(2\right)\\\dfrac{2m-1}{m^2-m}>0\left(3\right)\end{matrix}\right.\)
\(\left(2\right)\Leftrightarrow m^2-m>0\Rightarrow\left[{}\begin{matrix}m< 0\\m>1\end{matrix}\right.\) (I)
Kết hợp \(\left(2\right)\Rightarrow\left(3\right)\Leftrightarrow2m-1>0\Rightarrow m>\dfrac{1}{2}\)(II)
\(\left(1\right)\Leftrightarrow4m^2-4m+1-4m^2+4m=1\ge0\forall m\) (III)
Từ (I) (II) (III) \(\Rightarrow m>1\)
Kết luận nghiệm BPT m>1
b)
\(\left\{{}\begin{matrix}\left(m-2\right)^2-\left(m+3\right)\left(m-1\right)\ge0\left(1\right)\\\dfrac{m-2}{m+3}< 0\left(2\right)\\\dfrac{m-1}{m+3}>0\left(3\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow m^2-4m+4-m^2-2m+3=-6m+7\ge0\Rightarrow m\le\dfrac{7}{6}\)(I)
\(\left(2\right)\Leftrightarrow-3< m< 2\) (2)
\(\left(3\right)\Leftrightarrow\left[{}\begin{matrix}m< -3\\m>1\end{matrix}\right.\)(3)
Nghiệm Hệ BPT là: \(1< m\le\dfrac{7}{6}\)

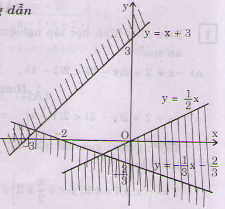
a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
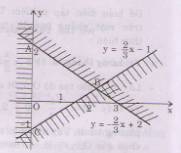
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).
\(\Leftrightarrow\left\{{}\begin{matrix}-4\le x\le1\\\left[{}\begin{matrix}x>1\\x< -2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow-4\le x< -2\)