Gỉai giúp nhé?!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BM
1
MH
27 tháng 3 2022
Ta có:
\(\dfrac{3}{10}>\dfrac{3}{15};\dfrac{3}{11}>\dfrac{3}{15};\dfrac{3}{12}>\dfrac{3}{15};\dfrac{3}{13}>\dfrac{3}{15};\dfrac{3}{14}>\dfrac{3}{15}\)
\(\Rightarrow S>1\) (*)
\(\dfrac{3}{10}< \dfrac{1}{3};\dfrac{3}{11}< \dfrac{1}{3};\dfrac{3}{12}< \dfrac{1}{3};\dfrac{3}{13}< \dfrac{1}{3};\dfrac{3}{14}< \dfrac{1}{3}\)
\(\Rightarrow S< \dfrac{5}{3}< 2\)(**)
Từ (*) và (**)
\(\Rightarrow1< S< 2\)
\(\Rightarrow\) S không là số tự nhiên
NN
1
9 tháng 3 2019
\(6x^4-2x^3-x^2+2=0\)
\(\Leftrightarrow6x^4-8x^3+4x^2+6x^3-8x^2+4x+3x^2-4x+2=0\)
\(\Leftrightarrow2x^2\left(3x^2-4x+2\right)+2x\left(3x^2-4x+2\right)+\left(3x^2-4x+2\right)=0\)
\(\Leftrightarrow\left(3x^2-4x+2\right)\left(2x^2+2x+1\right)=0\)
Mà \(2x^2+2x+1=2\left(x+\frac{1}{2}\right)^2 +\frac{1}{2}>0\forall x\)
\(3x^2-4x+2=3\left(x-\frac{2}{3}\right)^2+\frac{2}{3}>0\left(\forall x\right)\)
Do đó tập nghiệm của pt là: \(S=\varnothing\)
Chúc bạn học tốt.
NC
0
S
22 tháng 5 2021
TH1: \(x-2=5\) \(\Rightarrow x=7\) |
TH2: \(-x+2=5\) \(\Rightarrow x=-3\) |
22 tháng 5 2021
`|x-2|=5`
`<=>` $\\left[ \begin{array}{l}x-2=5\\x-3=-5\end{array} \right.$
`<=>` $\\left[ \begin{array}{l}x=7\\x=-2\end{array} \right.$
Vậy `s={7,-2}`
18 tháng 11 2019
\(\left|5+x\right|=3x+1\)
\(\left|5+x\right|=5+x\)khi \(5+x>0\Leftrightarrow x< -5\)
\(\left|5+x\right|=-\left(5+x\right)\)khi \(5+x\le0\Leftrightarrow x\le-5\)
Với x < - 5 ta có:
\(pt\Leftrightarrow5+x=3x+1\Leftrightarrow-2x=-4\Leftrightarrow x=2\) (thoả mãn)
Với: \(x\le-5\) ta có
\(pt\Leftrightarrow-\left(5+x\right)=3x+1\Leftrightarrow-5-x=3x+1\Leftrightarrow-4x=6\Leftrightarrow x=-\frac{3}{2}\) (loại)
Vậy tập nghiệm của phương trình này là : S = 2
(Làm ngu đó vì chưa chắc dạng)
18 tháng 11 2019
\(|5+x|=3x+1\)
\(\Leftrightarrow\orbr{\begin{cases}5+x=3x+1\\5+x=-3x-1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x-3x=1-5\\x+3x=-1-5\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}-2x=-4\\4x=-6\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=\frac{-3}{2}\end{cases}}\)
Vậy ...
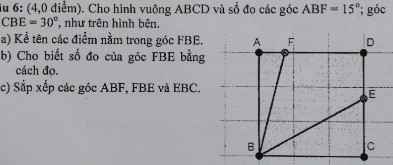
a: F,B,E,D
b; góc FBE=45 độ
c: góc ABF<góc CBE<góc FBE