
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tam giác ADB= tam giác CDB ( C-C-C)
Suy ra góc A=góc B
Góc D1 =góc D2
nên DB là tia phân giác góc ADC

Bạn kẻ thêm theo hình
1, để AB // CD thì cm B1=D2
Xét tg ABC và tg DBC:
AB = CD (gt)
AD = BC (gt)
BD cạnh chung
==> tg ABD = tg CBD ==> B1=D2, mà B1 và D2 ở vị trí so le trong ==> AB // CD
2, để AD // BC thì cm D1 = B2
Xét tg ADC và tg ABC:
AB = CD (gt)
AD = BC (gt)
AC cạnh chung
==> tg ADC = tg ABC ==> D1=B2, mà D1 và B2 ở vị trí so le trong ==> AD // BC
___________
Chúc bạn học tốt
Like / tick cho mình nếu đúng ạ ! cảm ơn ^^

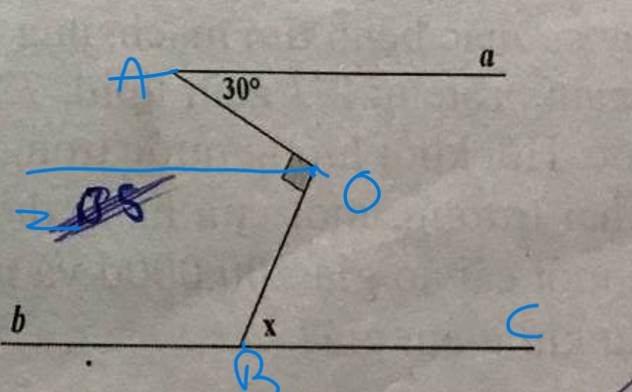
Qua O, kẻ tia Oz//Aa
Oz//Aa
Aa//BC
Do đó: Oz//BC
Oz//Aa
=>\(\widehat{zOA}=\widehat{OAa}\)(hai góc so le trong)
=>\(\widehat{zOA}=30^0\)
\(\widehat{zOA}+\widehat{zOB}=\widehat{AOB}=90^0\)
=>\(\widehat{zOB}=90^0-30^0=60^0\)
Oz//BC
=>\(\widehat{zOB}=\widehat{OBC}\)(hai góc so le trong)
=>\(x=60^0\)

Đặt tên các điểm, các tên đường thẳng như trên hình vẽ.
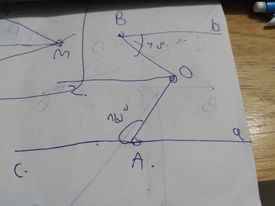
Qua O, kẻ tia Oz//Bb(Oz và Bb là hai tia nằm ở hai phía khác nhau)
Oz//Bb
=>\(\widehat{zOB}=\widehat{bBO}\)(hai góc so le trong)
=>\(\widehat{zOB}=40^0\)
Oz//Bb
Bb//Ac
=>Oz//Ac
=>\(\widehat{zOA}+\widehat{OAc}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{zOA}=180^0-120^0=60^0\)
\(\widehat{BOA}=\widehat{zOB}+\widehat{zOA}=60^0+40^0=100^0\)

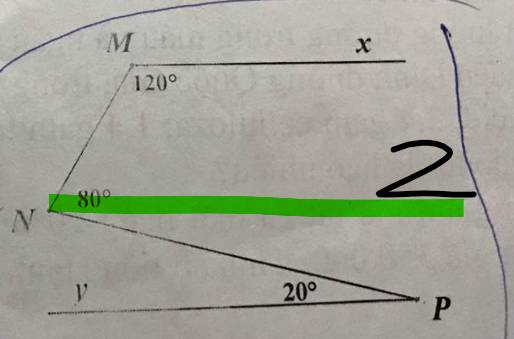
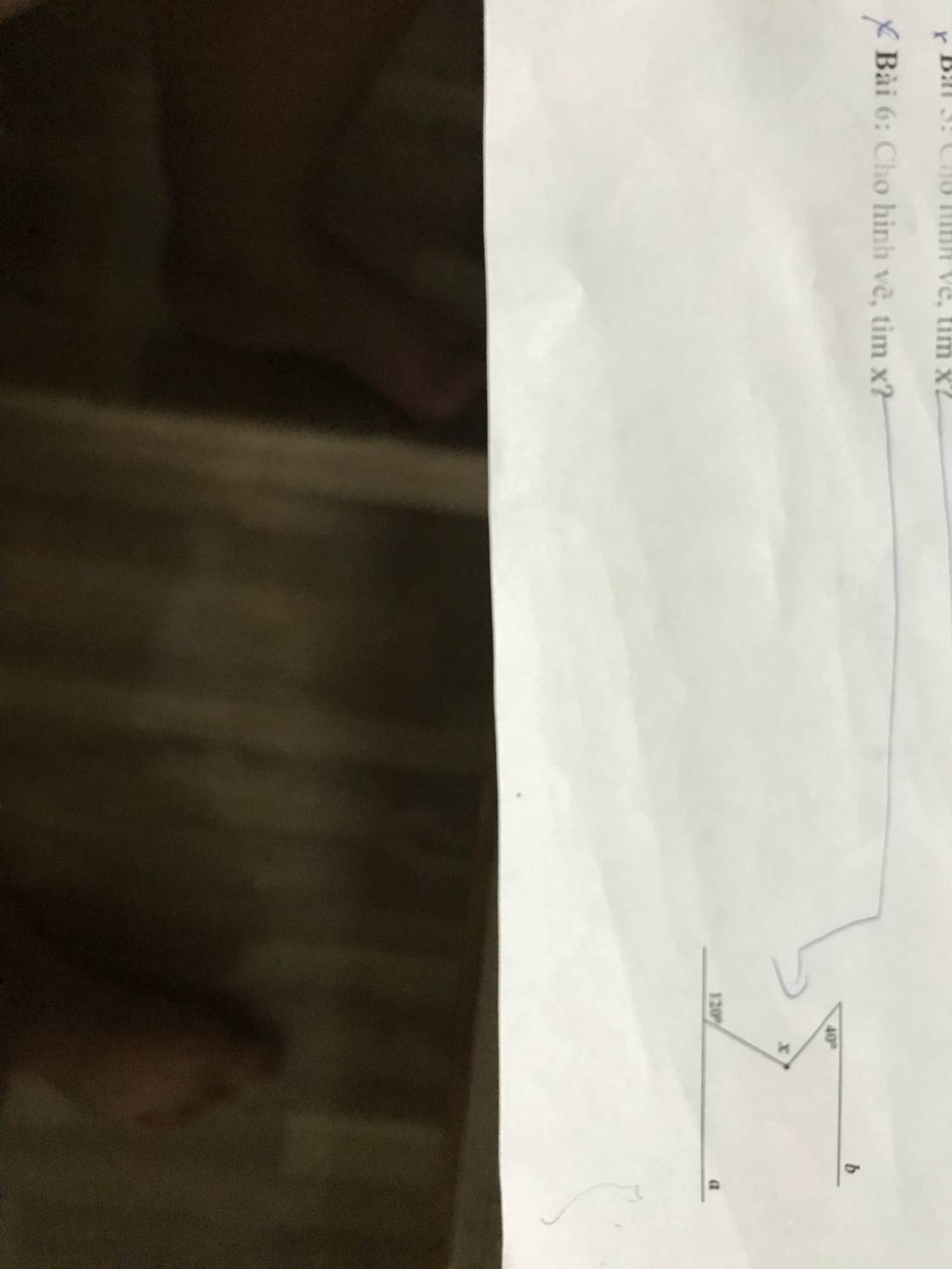
Qua N, kẻ tia Nz//Mx
Nz//Mx
=>\(\widehat{zNM}+\widehat{M}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{zNM}=60^0\)
\(\widehat{zNM}+\widehat{zNP}=\widehat{MNP}\)
=>\(\widehat{zNP}=80^0-60^0=20^0\)
\(\widehat{zNP}=\widehat{P}\)
mà hai góc này ở vị trí so le trong
nên Nz//Py
=>Mx//Py

\(\widehat{x'MC}=\widehat{xMN}\)(hai góc đối đỉnh
mà \(\widehat{xMN}=60^0\)
nên \(\widehat{x'MC}=60^0\)
Mz là phân giác của \(\widehat{x'MC}\)
=>\(\widehat{x'Mz}=\widehat{CMz}=\dfrac{60^0}{2}=30^0\)
Mz//Nt
=>\(\widehat{zMC}=\widehat{tNM}\)(hai góc đồng vị)
=>\(\widehat{tNM}=30^0\)
Nt là phân giác của góc y'NM
=>\(\widehat{y'NM}=2\cdot\widehat{tMN}=60^0\)

Bài 7:
a:
Ta có: ΔABC đều
=>AB=AC=BC và \(\widehat{BAC}=\widehat{ABC}=\widehat{ACB}=60^0\)
Xét ΔABC có \(\widehat{ACE}\) là góc ngoài tại đỉnh C
nên \(\widehat{ACE}=\widehat{CAB}+\widehat{CBA}=120^0\)
Xét ΔACE có \(\widehat{ACE}>90^0\)
nên AE là cạnh lớn nhất trong ΔACE
=>AE>AC
=>AE>AB
b: Xét ΔCAE có CA=CE(=BC)
nên ΔCAE cân tại C
=>\(\widehat{CAE}=\dfrac{180^0-120^0}{2}=30^0\)
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là phân giác của góc BAC
=>\(\widehat{HAC}=\dfrac{\widehat{BAC}}{2}=30^0\)
=>\(\widehat{HAC}=\widehat{CAE}\)
=>AC là phân giác của góc HAE
bài 9:
a: ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH\(\perp\)BC
b: Xét ΔAHM vuông tại H có AM là cạnh huyền
nên AM là cạnh lớn nhất trong ΔAHM
=>AM>AH
Xét ΔAHM có \(\widehat{AMB}\) là góc ngoài tại đỉnh M
nên \(\widehat{AMB}=\widehat{AHM}+\widehat{HAM}=90^0+\widehat{HAM}\)
=>\(\widehat{AMB}>90^0\)
Xét ΔAMB có \(\widehat{AMB}>90^0\)
nên AB là cạnh lớn nhất trong ΔAMB
=>AB>AM
=>AB>AM>AH
=>AC>AM>AH
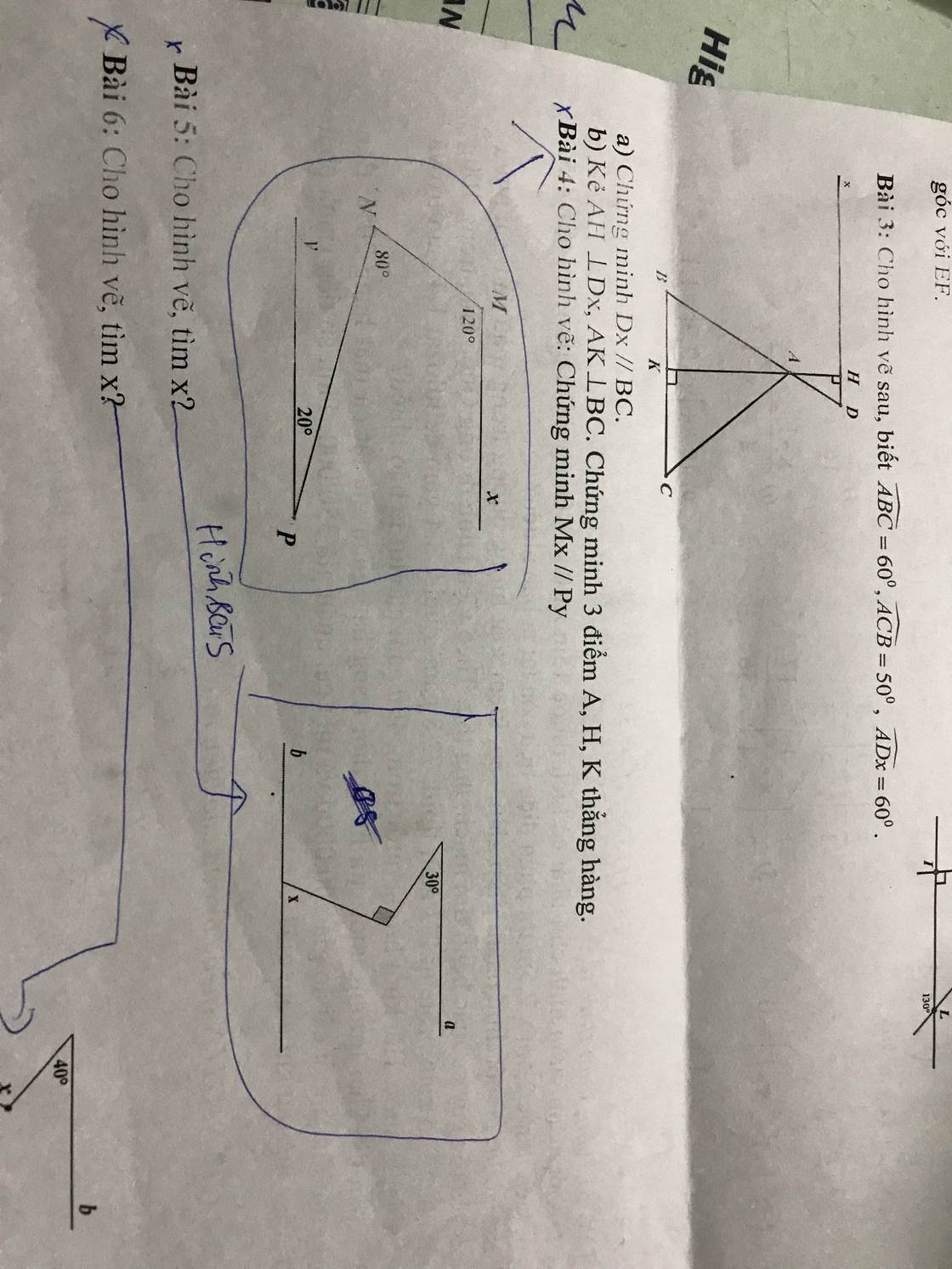







ko cần làm câu 6