K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Giúp mình với aa (Giải chi tiết + nếu được thì thêm lời giải thích ở cuối bài làm giúp mình nha 
)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
\(2\left(x-3\right)^4-3^2=503\\ \Rightarrow2\left(x-3\right)^4=512\\ \Rightarrow\left(x-3\right)^4=256\\ \Rightarrow\left[{}\begin{matrix}x-3=4\\x-3=-4\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=7\\x=-1\end{matrix}\right.\)
3T
1
18 tháng 6 2023
4:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
góc BAC=90 độ
=>ABDC là hcn
=>ΔACD vuông tại C
b: Xét ΔKAB vuông tại A và ΔKCD vuông tại C có
KA=KC
AB=CD
=>ΔKAB=ΔKCD
=>KB=KD
c: Xét ΔACD có
DK,CM là trung tuyến
DK cắt CM tại I
=>I là trọng tâm
=>KI=1/3KD
Xét ΔCAB có
AM,BK là trung tuyến
AM cắt BK tại N
=>N là trọng tâm
=>KN=1/3KB=KI
CK
1
7 tháng 5 2022
\(f(x)=ax^2+bx+6\)
Để \(f(x)\) là đa thức bậc \(1\) thì \(ax^2=0\)
\(→a=0\)
Thay \(x=1\) vào \(f(x)=ax^2+bx+6\)
\(f(1)=b.1+6=b+6\)
Mà \(f(1)=3\)
\(\Rightarrow b+6=3\Rightarrow b=3−6\Rightarrow b=−3\)
Vậy \(a=0;b=−3\)
giải giúp mình với ko cần giải bài 13
24 tháng 8 2021
Bài 11:
d. áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{2x+5y}{6+20}=\dfrac{10}{26}=\dfrac{5}{13}\)
\(\dfrac{x}{3}=\dfrac{5}{13}\Rightarrow x=\dfrac{15}{13}\\ \dfrac{y}{4}=\dfrac{5}{13}\Rightarrow y=\dfrac{20}{13}\)
e. \(\dfrac{2x}{3y}=-\dfrac{1}{3}\Leftrightarrow\dfrac{2x}{-1}=\dfrac{3y}{3}\Leftrightarrow\dfrac{-2x}{1}=\dfrac{3y}{3}\)
áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{-2x}{1}=\dfrac{3y}{3}=\dfrac{-2x+3y}{1+3}=\dfrac{7}{4}\)
\(\dfrac{-2x}{1}=\dfrac{7}{4}\Rightarrow x=-\dfrac{7}{8}\\ \dfrac{3y}{3}=\dfrac{7}{4}\Rightarrow y=\dfrac{7}{4}\)
f. \(x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{1}\)
áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}=\dfrac{y}{1}=\dfrac{x-y}{3-1}=\dfrac{16}{2}=8\)
\(\dfrac{x}{3}=8\Rightarrow x=24\\ \dfrac{y}{1}=8\Rightarrow y=8\)
28 tháng 7 2023
2:
a: =2xy^4+12xy^4+x^2=14xy^4+x^2
b: 3a^2b^3+ab-8a^2b^3-2ab
=ab-2ab+3a^2b^3-8a^2b^3
=-5a^2b^3-ab
3:
a: BC=căn 3^2+4^2=5cm
b: Xét ΔABD vuông tại A và ΔABC vuông tại A có
AB chung
AD=AC
=>ΔABD=ΔABC
c: Xét ΔBEA vuông tại E và ΔBFA vuông tại F có
BA chung
góc EBA=góc FBA
=>ΔBEA=ΔBFA
=>EA=FA
=>ΔAEF cân tại A
giải giúp mình với
AH
Akai Haruma
Giáo viên
5 tháng 9 2021
Bài 7:
Gọi số hs lớp 7A, 7B, 7C lần lượt là $a,b,c$
Theo bài ra ta có: $\frac{a}{10}=\frac{b}{9}=\frac{c}{8}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{a}{10}=\frac{b}{9}=\frac{c}{8}=\frac{a-c}{10-8}=\frac{10}{2}=5$
$\Rightarrow a=10.5=50; b=9.5=45; c= 8.5=40$ (học sinh)
AH
Akai Haruma
Giáo viên
5 tháng 9 2021
Bài 8:
Gọi số kg giấy tổ I, II, III thu được lần lượt là $a,b,c$
Theo bài ra ta có:
$\frac{a}{2}=\frac{b}{4}=\frac{c}{5}$ và $a+c-b=27$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{a}{2}=\frac{b}{4}=\frac{c}{5}=\frac{a+c-b}{2+5-4}=\frac{27}{3}=9$
$\Rightarrow a=2.9=18; b=4.9=36; c=5.9=45$ (kg)
Giải:
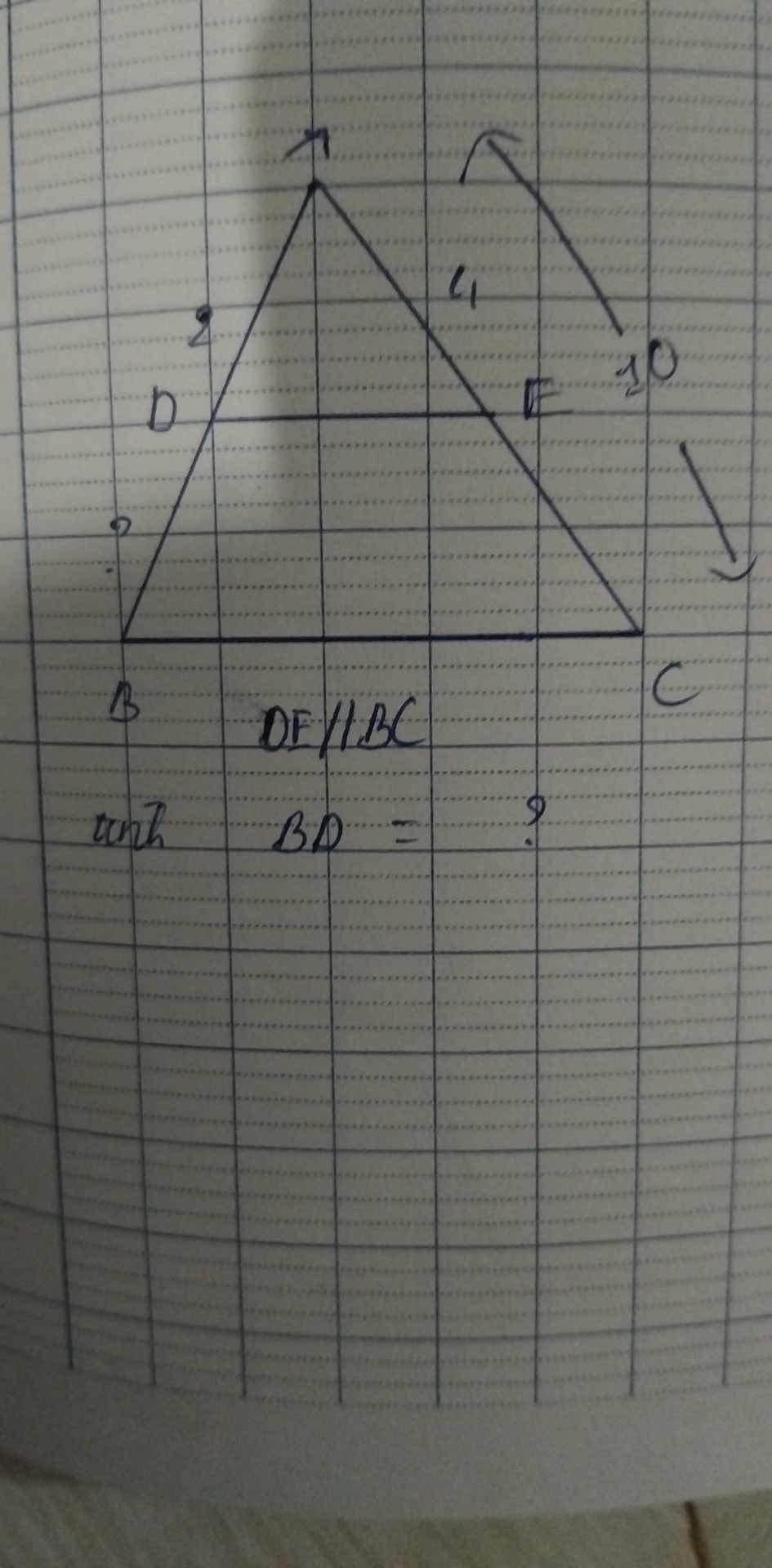
Vì DE // BC
\(\dfrac{AD}{AB}\) = \(\dfrac{AE}{AC}\) (hệ quả Thalet)
⇒ \(\dfrac{2}{AB}\) = \(\dfrac{4}{10}\)
AB = 2 : \(\dfrac{4}{10}\)
AB = 5
Vậy AB = 5 cm
AB = AD + BD
BD = AB - AD
BD = 5 - 2 = 3
Vậy BD = 3cm
Kết luận: BD = 3cm
Ta có:
EC = AC - AE = 10 - 4 = 6
∆ABC có:
DE // BC (gt)
⇒ AD/BD = AE/EC (định lý Thales)
⇒ 2/BD = 4/6
⇒ BD = 2 . 6 : 4 = 3