
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


12.
\(y=\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\le\sqrt[]{2}\)
\(\Rightarrow M=\sqrt{2}\)
13.
Pt có nghiệm khi:
\(5^2+m^2\ge\left(m+1\right)^2\)
\(\Leftrightarrow2m\le24\)
\(\Rightarrow m\le12\)
14.
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=-\dfrac{5}{3}\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow x=k2\pi\)
15.
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(3\right)+k\pi\end{matrix}\right.\)
Đáp án A
16.
\(\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{6}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
\(\left[{}\begin{matrix}2\pi\le\dfrac{\pi}{3}+k2\pi\le2018\pi\\2\pi\le\pi+k2\pi\le2018\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}1\le k\le1008\\1\le k\le1008\end{matrix}\right.\)
Có \(1008+1008=2016\) nghiệm

a. Ta có : \(SA\perp\left(ABCD\right)\Rightarrow BC\perp SA\)
Đáy ABCD là HV \(\Rightarrow BC\perp AB\)
Suy ra : \(BC\perp\left(SAB\right)\Rightarrow\left(SAB\right)\perp\left(SBC\right)\) ( đpcm )
b. \(\left(SBD\right)\cap\left(ABCD\right)=BD\)
O = \(AC\cap BD\) ; ta có : \(AO\perp BD;AO=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{2}a\)
Dễ dàng c/m : \(BD\perp\left(SAC\right)\) \(\Rightarrow SO\perp BD\)
Suy ra : \(\left(\left(SBD\right);\left(ABCD\right)\right)=\left(SO;AO\right)=\widehat{SOA}\)
\(\Delta SAO\perp\) tại A có : tan \(\widehat{SOA}=\dfrac{SA}{AO}=\dfrac{a}{\dfrac{\sqrt{2}}{2}a}=\sqrt{2}\)
\(\Rightarrow\widehat{SOA}\approx54,7^o\) \(\Rightarrow\) ...

1.
\(\Leftrightarrow1+2sin\dfrac{x}{2}cos\dfrac{x}{2}+\sqrt{3}cosx=3\)
\(\Leftrightarrow sinx+\sqrt{3}cosx=2\)
\(\Leftrightarrow\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=1\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{6}\right)=1\)
\(\Leftrightarrow x-\dfrac{\pi}{6}=k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k2\pi\)
2.
\(cos2x=-1\)
\(\Leftrightarrow2x=\pi+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
3.
\(\left(2sinx-cosx\right)\left(1+cosx\right)=\left(1+cosx\right)\left(1-cosx\right)\)
\(\Leftrightarrow\left(1+cosx\right)\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Nghiệm dương nhỏ nhất là \(x=\dfrac{\pi}{6}\)
4.
\(1-cos2x-1-cos6x=0\)
\(\Leftrightarrow cos6x=-cos2x=cos\left(\pi-2x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}6x=\pi-2x+k2\pi\\6x=2x-\pi+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\\x=-\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\)
Pt có 6 nghiệm trên khoảng đã cho

6.
\(sin3x+cos2x=1+sin3x-sinx\)
\(\Leftrightarrow cos2x=1-sinx\)
\(\Leftrightarrow1-2sin^2x=1-sinx\)
\(\Leftrightarrow2sin^2x-sinx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
7.
\(\sqrt{2}sinx-2\sqrt{2}cosx=2-2sinx.cosx\)
\(\Leftrightarrow\sqrt{2}sinx\left(\sqrt{2}cosx+1\right)-2\left(\sqrt{2}cosx+1\right)=0\)
\(\Leftrightarrow\left(\sqrt{2}sinx-2\right)\left(\sqrt{2}cosx+1\right)=0\)
\(\Leftrightarrow cosx=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow x=\pm\dfrac{3\pi}{4}+k2\pi\)
\(\left(\dfrac{3\pi}{4}\right).\left(-\dfrac{3\pi}{4}\right)=-\dfrac{9\pi^2}{16}\)
8.
\(2sinx.cosx+3cosx=0\)
\(\Leftrightarrow cosx\left(2sinx+3\right)=0\)
\(\Leftrightarrow cosx=0\)
\(\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
\(\Rightarrow x=\dfrac{\pi}{2}\) có 1 nghiệm trong khoảng đã cho
9.
\(cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\)
\(\Rightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Đáp án D

\(2cosx+\sqrt{2}=0\Leftrightarrow cosx=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3\pi}{4}+k2\pi\\x=-\dfrac{3\pi}{4}+n2\pi\end{matrix}\right.\)
\(-6< x< 6\Rightarrow\left\{{}\begin{matrix}-6< \dfrac{3\pi}{4}+k2\pi< 6\\-6< -\dfrac{3\pi}{4}+n2\pi< 6\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-1,33< k< 0,58\\-0,58< n< 1,33\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}k=\left\{-1;0\right\}\\n=\left\{0;1\right\}\end{matrix}\right.\) \(\Rightarrow\) có 4 nghiệm

Rất đơn giản, điểm \(A\left(1;-2\right)\) có \(x=1;y=-2\)
Do đó ảnh của nó qua phép biến hình \(f\) sẽ có tọa độ: \(\left\{{}\begin{matrix}x_{A'}=-x=-1\\y_{A'}=\dfrac{y}{2}=-1\end{matrix}\right.\)
\(\Rightarrow A'\left(-1;-1\right)\)

Hoàn toàn không dịch được các kí hiệu mà bạn ghi
Để ghi kí hiệu tổ hợp bạn sử dụng công cụ soạn thảo này:

Sau đó gõ chữ hoa cần ghi (ví dụ C nếu muốn tổ hợp, A nếu muốn chỉnh hợp) rồi chọn tiếp chỗ này:
Sau đó chọn:
Rồi ghi giá trị k, n vào 2 ô nhỏ trên dưới là được

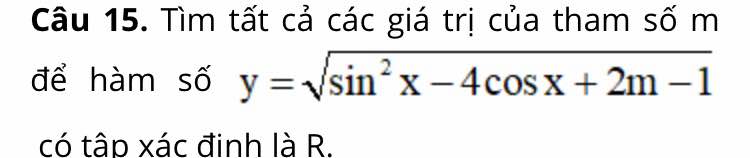


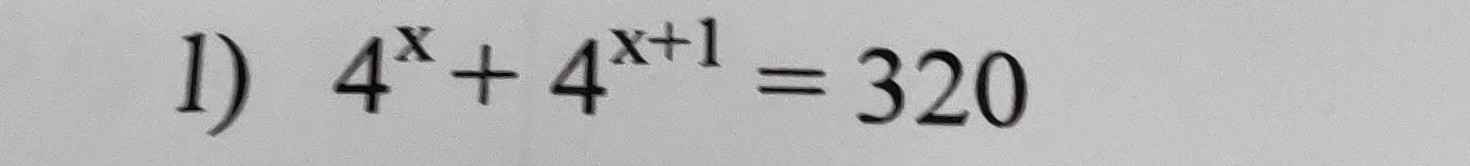





 Giải giúp mình với ạ
Giải giúp mình với ạ
Điều kiện để biểu thức điều kiện có nghĩa: \(n\ge3\)
Giả thiết tương đương:
\(\dfrac{n!}{\left(n-3\right)!}+\dfrac{6.n!}{\left(n-2\right)!.2!}-4n=100\)
\(\Leftrightarrow n\left(n-1\right)\left(n-2\right)+3n\left(n-1\right)-4n-100=0\)
\(\Leftrightarrow n^3-5n-100=0\)
\(\Leftrightarrow\left(n-5\right)\left(n^2+5n+20\right)=0\)
\(\Leftrightarrow n=5\)
Do đó nhị thức có dạng: \(\left(x^2+2\right)^{15}\)
Số hạng tổng quát trong khai triển: \(C_{15}^k\left(x^2\right)^k.2^{15-k}=C_{15}^k.2^{15-k}x^{2k}\)
Số hạng chứa \(x^8\) thỏa mãn: \(2k=8\Rightarrow k=4\)
Hệ số: \(C_{15}^4.2^{11}\)
Anh ơi em nhắn tin cho anh ở mục tin nhắn anh vào xem nhá