Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

< Bạn tự vẽ hình nha>
a)Xét ΔABE và ΔACF, ta có:
góc A: chung
góc F=góc E= 90o
Vậy ΔABE ∼ ΔACF (g.g)
b)Xét ΔHEC và ΔHFB là:
góc H: chung
H1=H2(đối đỉnh)
Vậy ΔHEC∼ ΔHFB (g.g)
⇒\(\dfrac{HE}{HF}\)=\(\dfrac{HC}{HB}\)⇔HE.HB=HF.HC
<Mình chỉ biết đến đó thôi>![]()

Mình chỉ biết làm mỗi câu d thôi bạn thông cảm nhé !!!
d) Vì BE vuông AC, CF vuông AB(gt)
Mà BE, CF cắt nhau tại H
=> H là trực tâm của tam giác ABC
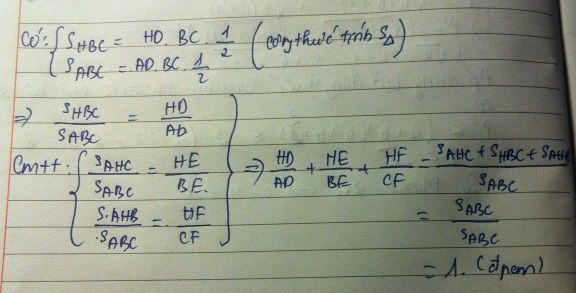
Ta có Sbhc/Sabc = 1/2 x HD xBC/1/2 x AD x BC = HD/AD (1)
Ta có Sahc/Sabc = 1/2 x HE x AC/1/2 x BE x AC = HE/BE (2)
Ta có Sabh/Sabc = 1/2 x HF x AB/1/2 x CF x AB = HF/CF (3)
Từ (1), (2), (3) => HD/AD + HE/BE + HF/CF = Sbhc/Sabc + Sahc/Sabc + Sabh/Sabc
=> HD/AD + HE/BE + HF/CF = Sabc/Sabc
=> HD/AD + HE/BE + HF/CF = 1 (Đpcm)
câu c nè
Chứng minh tgCEB đồng dạng vs tgCDA (g.g)=>gócEBC= gócDAC
Do đó : tg ADC đồng dạng với tam giác BDH=>AD/BD=DC/DH
=>BD/DH=AD/DC=>BD/DH=3/4(AD PYTAGO vào tg vuông ADC ta tính được DC=4)
vậy\(\frac{BD}{DH}=\frac{3}{4}\)

a) Xét tam giác ABE và tam giác ACF có:
góc AEB = góc AFC (= 90 độ)
góc A chung
=> tam giác ABE \(\sim\) tam giác ACF (gg)
=> \(\dfrac{AB}{AC}=\dfrac{AF}{AE}\) (các cạnh t/ứng tỉ lệ)
=> AB . AE = AC . AF
a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
gsoc A chung
Do đó: ΔABE đồng dạng với ΔACF
SUy ra: AE/AF=AB/AC
hay \(AE\cdot AC=AB\cdot AF;\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
b: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc A chung
Do đó: ΔAEF đồng dạng với ΔaBC
Suy ra: góc AFE=góc ACB





Tự vẽ hình nha
a) Xét 2 tam giác vuông ADC và BEC có:
\(\widehat{D}=\widehat{E}=1v\)
\(\widehat{C}\) chung
\(\Rightarrow\Delta ADC\) đồng dạng \(\Delta BEC\)
b) Xét 2 tam giác vuông HEA và HDB có:
\(\widehat{AHE}=\widehat{BHD}\)(đối đỉnh)
\(\widehat{D}=\widehat{E}=1v\)
\(\Rightarrow\Delta HEA\) đồng dạng \(\Delta HDB\)
\(\Rightarrow\)\(\dfrac{HE}{HD}=\dfrac{HA}{HB}\Rightarrow HE.HB=HA.HD\)
c) Vì H là trực tâm nên \(CF\perp AB\)
\(\Rightarrow\widehat{F}=1v\)
Xét 2 tam giác vuông AFH và ADB có:
\(\widehat{F}=\widehat{D}=1v\)
\(\widehat{H}=\widehat{B}\)(cùng phụ với \(\widehat{A}\))
\(\Rightarrow\Delta AFH\:\) đồng dạng \(\Delta ADB\)
\(\Rightarrow\)\(\dfrac{AF}{AD}=\dfrac{AH}{AB}\Rightarrow AF.AB=AH.AD\)
d) Bạn ghi thiếu đề. Chứng minh tổng đó bằng ............
\(\dfrac{S_{HDC}}{S_{ADC}}=\dfrac{\dfrac{1}{2}.HD.DC}{\dfrac{1}{2}.AD.DC}=\dfrac{HD}{AD}\)
\(\dfrac{S_{BDH}}{S_{BDA}}=\dfrac{\dfrac{1}{2}.BD.DH}{\dfrac{1}{2}.BD.AD}=\dfrac{HD}{AD}\)
\(\Rightarrow\)\(\dfrac{S_{HDC}}{S_{ADC}}=\dfrac{S_{BDH}}{S_{BDA}}=\dfrac{S_{HDC}+S_{BDH}}{S_{ADC}+S_{BDA}}=\dfrac{S_{BHC}}{S_{ABC}}=\dfrac{HD}{AD}\)
Tương tự: \(\dfrac{HE}{BE}=\dfrac{S_{AHC}}{S_{ABC}};\dfrac{HF}{CF}=\dfrac{S_{AHB}}{S_{ABC}}\)
\(\Rightarrow\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=\dfrac{S_{BHC}}{S_{ABC}}+\dfrac{S_{AHC}}{S_{ABC}}+\dfrac{S_{AHB}}{S_{ABC}}=\dfrac{S_{BHC}+S_{AHC}+S_{AHB}}{S_{ABC}}=\dfrac{S_{ABC}}{S_{ABC}}=1\)