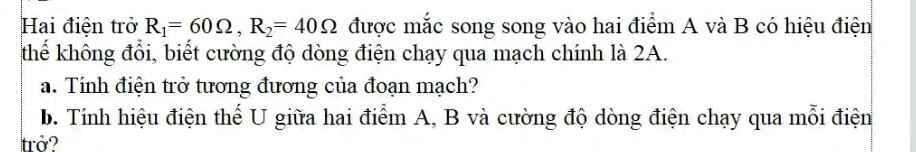K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 1 2022
a) Điện trở tương đương của đoạn mạch :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.40}{60+40}=24\left(\Omega\right)\)
b) Hiệu điện thế giữa hai đầu đoạn mạch :
\(U=I.R_{tđ}=2.24=48\left(V\right)\)
⇒ \(U=U_1=U_2=48\left(V\right)\) (vì R1 // R2)
Cường độ dòng điện chạy qua mỗi điện trở :
\(I_1=\dfrac{U_1}{R_1}=\dfrac{48}{60}=0,8\left(A\right)\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{48}{40}=1,2\left(A\right)\)
Chúc bạn học tốt
N
6 tháng 12 2021
Bài 1:
\(\left\{{}\begin{matrix}R=\dfrac{U^2}{P}=\dfrac{220^2}{1500}=\dfrac{484}{15}\Omega\\I=\dfrac{P}{U}=\dfrac{1500}{220}=\dfrac{75}{11}A\end{matrix}\right.\)
\(A=UIt=220\cdot\dfrac{75}{11}\cdot3=4500\)Wh = 4,5kWh
\(H=\dfrac{Q_{thu}}{Q_{toa}}100\%=>Q_{toa}=\dfrac{Q_{thu}}{H}100\%=\dfrac{2\cdot4200\cdot75}{80}100\%=787500\left(J\right)\)
Ta có: \(Q_{toa}=A=UIt=>t=\dfrac{Q_{toa}}{UI}=\dfrac{787500}{220\cdot\dfrac{75}{11}}=525\left(s\right)\)
DD
0
TP
1
21 tháng 4 2022
mình giải rồi nhé, bạn có thể lướt xuống để nhận lời giải
5 tháng 12 2021
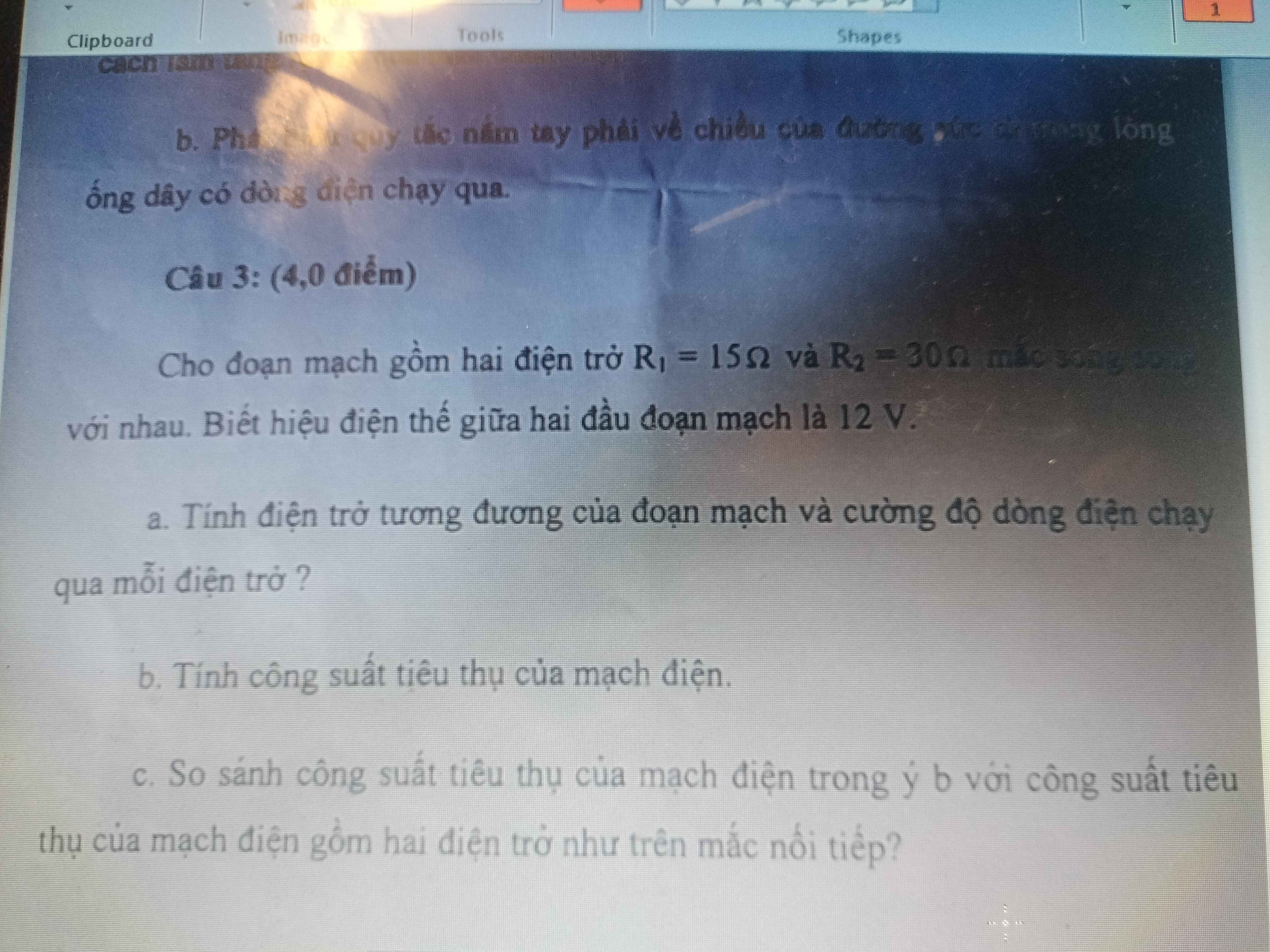
\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)