Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

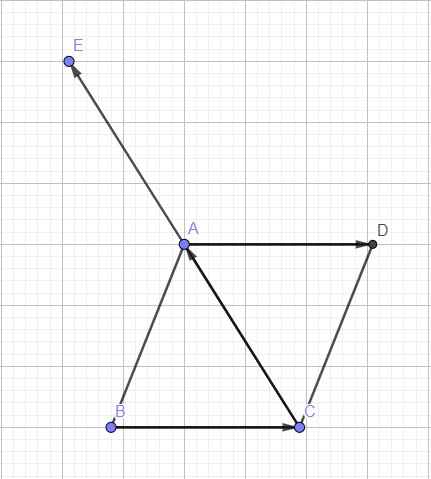
\(\overrightarrow{AD}=\overrightarrow{BC}\) \(\Rightarrow\) ABCD là hình bình hành
Vậy D là đỉnh của hình bình hành ABCD
\(\overrightarrow{AE}=\overrightarrow{CA}\Rightarrow\overrightarrow{AE}-\overrightarrow{CA}=\overrightarrow{0}\Rightarrow\overrightarrow{AE}+\overrightarrow{AC}=\overrightarrow{0}\)
\(\Rightarrow A\) là trung điểm CE hay E là điểm đối xứng C qua A

\(\left|\overrightarrow{BC}\right|=BC=\sqrt{AB^2+AC^2}=5\)

Chọn C.
Gọi D là điểm thỏa mãn tứ giác ABDC là hình chữ nhật.
Ta có ![]()
![]()

Ta có I CA+AB I = I CB I =CB
Xét tam giác ABC ( A=90 ) áp dụng định lý pytago có
CB^2 = AB^2 + AC^2 = 9+16=25 => CB=5.
Vậy I CA+AB I= I CB I =5
Bạn lưu ý lần sau gõ lời giải bằng công thức toán (biểu tượng \(\sum\) góc trái khung soạn thảo) để được tick dễ dàng hơn khi làm đúng nhé.

\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=BC=4\)

Lời giải:
Vì $\frac{AB}{AC}=\frac{3}{4}$ nên đặt $AB=3a; AC=4a$ $(a>0$)
Áp dụng hệ thức lượng trong tam giác vuông ta có:
$\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{AH^2}$
$\Rightarrow \frac{1}{(3a)^2}+\frac{1}{(4a)^2}=\frac{1}{16^2}$
$\Rightarrow \frac{25}{144a^2}=\frac{1}{16^2}$
$\Rightarrow a=\frac{20}{3}$
Áp dụng định lý pitago:
$HC=\sqrt{AC^2-AH^2}=\sqrt{(4a)^2-16^2}=\sqrt{(\frac{80}{3})^2-16^2}=\frac{64}{3}$ (cm)

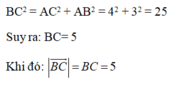
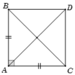
A B C B'
Dựng điểm B' sao cho C là trung điểm BB', suy ra \(\overrightarrow{BC}=\overrightarrow{CB'}\).
\(\left(\overrightarrow{CA},\overrightarrow{BC}\right)=\left(\overrightarrow{CA},\overrightarrow{CB'}\right)=\widehat{ACB'}\).
\(BC^2=\sqrt{AB^2+AC^2}=5\).
\(cos\widehat{BCA}=\dfrac{3}{5}\).
\(cos\left(\overrightarrow{CA},\overrightarrow{BC}\right)=cos\left(\overrightarrow{CA},\overrightarrow{CB'}\right)=cos\widehat{ACB'}=-\dfrac{3}{5}\).